摘要：
2018 年“雙 11”的交易額又達到了一個歷史新高度 2135 億。相比十年前，我們的交易額增長了 360 多倍，而交易峰值增長了 1200 多倍。相對應的，系統數呈現爆發式增長。系統在支撐“雙 11”過程中的複雜度和難度呈現指數級形式上升趨勢。

作為阿里巴巴全集團範圍的容器排程系統，Sigma 在“雙11”期間成功支撐了全集團所有容器（交易線中介軟體、資料庫、廣告等 20 多個業務）的調配，是阿⾥巴巴運維繫統重要的底層基礎設施。Sigma 已經是阿里全網所有機房線上服務管控的核心角色，管控的宿主機資源達到百萬級，重要程度不言而喻，其演算法的優劣程度影響了集團整體的業務穩定性，資源利用率。

當用戶向排程系統申請容器所需的計算資源(如 CPU 、 記憶體、磁碟)時，排程器負責挑選出滿足各項規格要求的物理機來部署這些容器。在相同的資源需求下，排程策略的優劣決定著叢集計算資源利用的水平。本文將簡要介紹群體增強學習演算法在排程策略優化中的應用。

作者：
王孟昌 達摩院機器智慧技術演算法專家
韓堂 阿里巴巴集團技術專家

1.計算資源排程及線上策略

當用戶向 Sigma 申請容器所需的計算資源（如 CPU、Memory、磁碟等）時，排程器負責挑選出滿足各項規格要求的物理機來部署這些容器。通常，滿足各項要求的物理機並非唯一，且水位各不相同，不同的分配方式最終得到的分配率存在差異，因此，排程器的一項核心任務就是按照某一策略從眾多候選機器中挑出最合適的物理機。

在文獻中，計算資源排程一般被表述為向量裝箱問題(vector bin packing problem)，如果各應用的容器數量事先已知（如大促場景），排程器可一次性為所有容器生成優化的排布方案，此時問題可以表述為整數規劃，可使用通用求解器或專門開發的演算法來求解；如果各應用的請求陸續到達 Sigma （如日常場景），排程器需要在每次請求到達時即時（線上）生成部署決策，此時問題可表述為馬爾可夫決策過程 (Markov Decision Process, MDP)，原則上可以通過值迭代或策略迭代求得最優策略。

最常用的排程策略包括 First-Fit (FF) 和 Best-Fit (BF)。如果使用 First-Fit演算法，排程器會將容器部署到遍歷中碰到的第一個滿足所有要求的物理機上；而Best-Fit演算法則會在滿足要求的物理機中挑選分配水位最高的機器來部署容器。對於經典的 bin packing 問題（即一維向量裝箱問題），First-Fit 和 Best-Fit 的近似比均為1.7，即二者都可保證所使用的機器數不超出最優方案的170%；對於2維及以上的向量裝箱問題，理論上不存在有著明確近似比保證的多項式演算法。當物理機的某個資源維度明顯為瓶頸而導致其它資源維度普遍有剩餘時，其有效維度可視為1，使用 First-Fit 或 Best-Fit 一般可以取得不錯的分配率；而一旦瓶頸並未集中體現在同一維度，兩種策略的效果就要大打問號了。

除了資源維度上的要求，實際排程中還有容災和干擾隔離上的考慮：比如同一應用的容器不允許全部部署到同一臺物理機上，很多應用甚至每臺機器上只允許有一個例項；某些應用之間還存在互斥關係（如資源爭搶），嚴重影響應用的效能，因此也不允許它們被部署到同一物理機上。這些限制條件的引入，使得常用策略越發水土不服了。通過人肉反覆試錯，勉強扛住了多次大促建站的壓力。然而，隨著各業務的擴張，線上容器的規模越來越大，資源變得越來越緊張，人肉調參的效率漸漸力不從心。

為了把排程同學從調參中解放出來，讓有限的資源扛住更大的壓力，達摩院機器智慧技術實驗室（M.I.T.）的決策智慧演算法團隊和Sigma排程團隊展開了緊密合作，對線上排程策略問題進行了研究，並開發了基於群體增強學習（SwarmRL）的演算法。

2.線上排程模型

記當前待部署容器的規格為向量 p∈P，為其分配資源時叢集狀態為向量 s∈S , 候選物理機的集合為 A⊆A，策略可表示為函式 π:S×P→A（π∈Π）。當按策略 π 選擇物理機 a=π(s,p)來部署該容器時，該選擇的即時成本為 r(a)，叢集的新狀態 s′ 由狀態量 s 、p 以及動作 a 共同決定，記為 s′=L(s,p,a) ；記後續到達的容器規格 p′， 對於線上排程，p′ 為隨機量。引入折扣係數 γ∈[0,1]，系統的 Bellman 方程為：

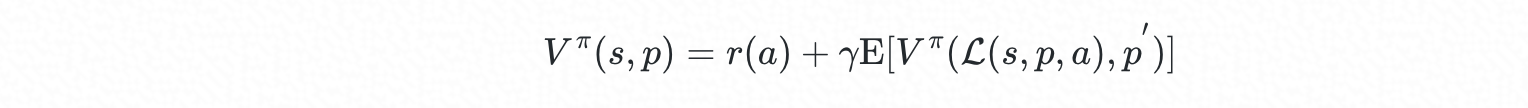
最優排程策略可表示為：

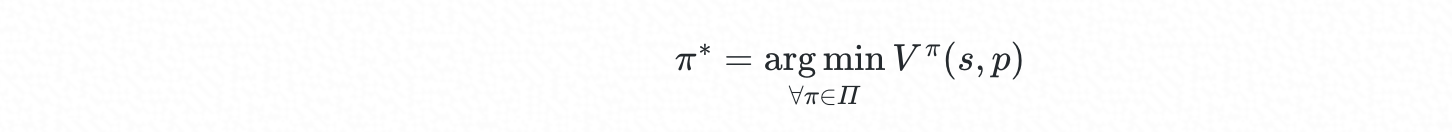
理論上，通過隨機梯度下降，我們可以在策略空間 Π 中搜索較優的策略，但相要更進一步的優化，甚至得到全域性最優策略，則需要藉助其它方法，特別是當最優策略可能是 multi-modal 形式。

3.群體增強學習 SwarmRL

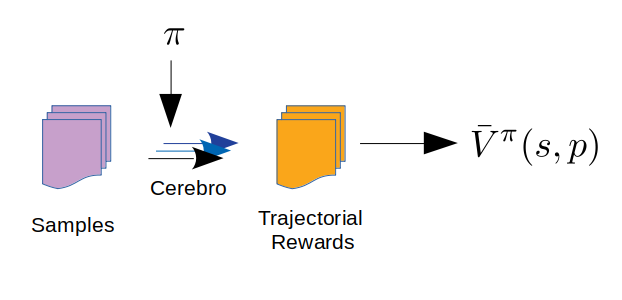
為防止策略的優化陷入較差的區域性最優解，同時擁有較快的收斂速度，我們基於群體增加學習的框架來設計演算法。與傳統的增強學習方法相比，演算法使用多個 agent 來探索問題的策略空間，且多個 agent 之間存在互相學習機制，這使得演算法有了跳出區域性陷阱的能力。為獲取各狀態值（V^π^）的估計，一個準確的 Sigma 模擬器必不可少，團隊內部同學基於 Sigma 的排程器開發了“完全保真”的模擬器 Cerebro 。

演算法首先隨機初始化一群 agent 的策略，針對每個策略，通過模擬器獲取相應的的狀態值估計，記錄當前全域性最佳策略。在後續的每次迭代中，各個 agent 不斷更新自身的區域性最佳策略，並參照區域性最佳策略與群體當前全域性最佳策略，對 agent 自身的當前策略進行更新，再進行模擬，獲取新策略的狀態值估計，更新全域性最佳策略。如此迴圈，直到滿足收斂條件。

在各個 agent 狀態值的估計中，樣本（多個隨機抽取的叢集快照和擴容請求序列）和各 agent 的當前策略被輸入模擬器 Cerebro，追蹤模擬時叢集狀態的軌跡，即可得到該軌跡的總成本；基於多個樣本的軌跡總成本求平均，即得到相應策略下的狀態估計值。

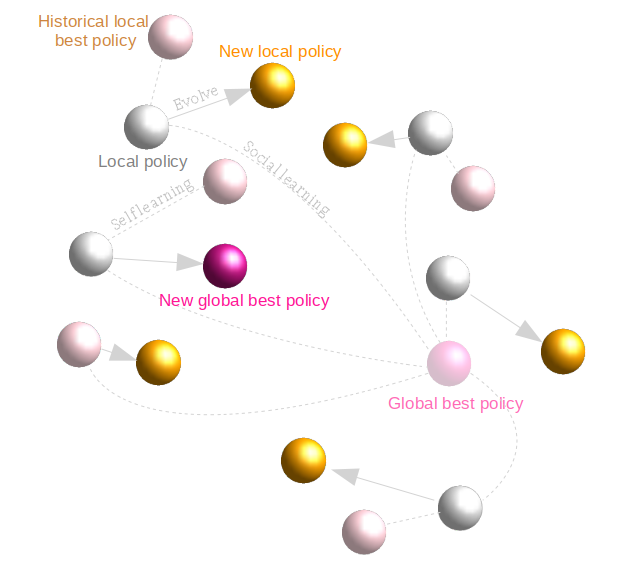
在 SwarmRL 中，策略的演進方向與步長用“速度” (v) 來表示，速度的變化涉及區域性最佳策略 (π^L) 和群體全域性最佳策略 (π^G ) 與 agent 當前策略 (π) 的差異，並受策略慣性因子 w、本地學習因子C~1~（self-learning）、群體學習因子 C~2~ (social-learning) 等引數的調控：

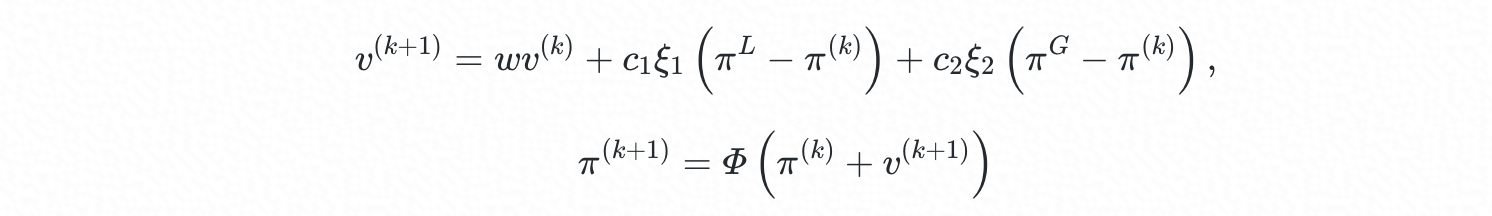
其中 ξ1,ξ2∈[0,1] 為隨機量，Φ為可行性保持對映，用於將逸出可行域的 agent 重新“拉回”可行域。在迭代中，區域性最佳策略 (π^L) 和群體全域性最佳策略 (π^G ) 不斷更新：

4.演算法應用

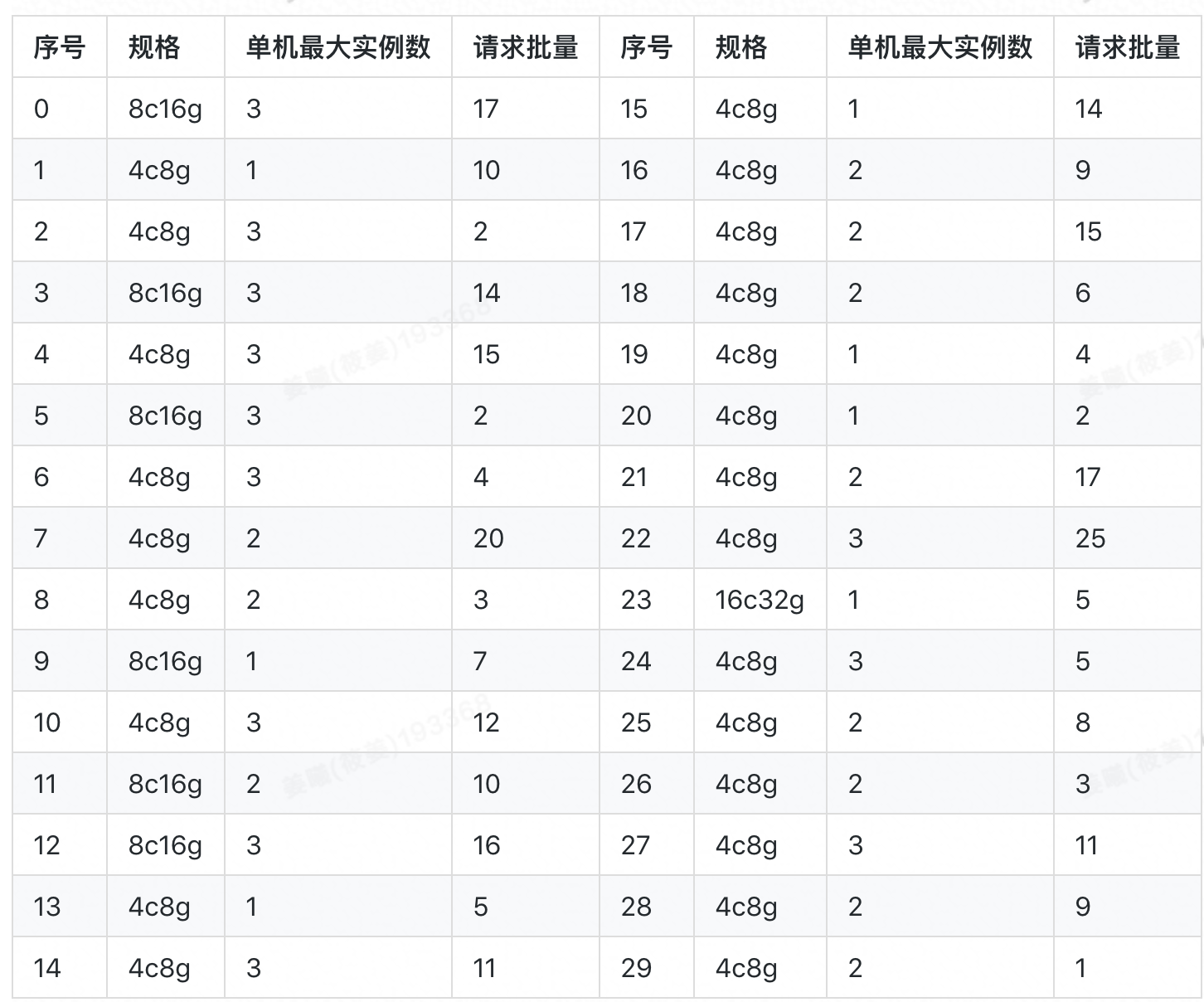
下面我們先用一個隨機生成的小算例來對比一下演算法的效果。算例中涉及 30 個應用（見下表），其容器規格主要為 4c8g 與 8c16g，所用宿主機的規格均為 96c512g。

若在排程時，請求的順序和數量均為已知（“上帝視角”），即進行事後排布，使用整數規劃求得的最優解對應的分配率為 94.44 % （這也是所有排程策略在該算例上所得分配率的上界），共啟用 15 臺宿主機，具體排布方案為：

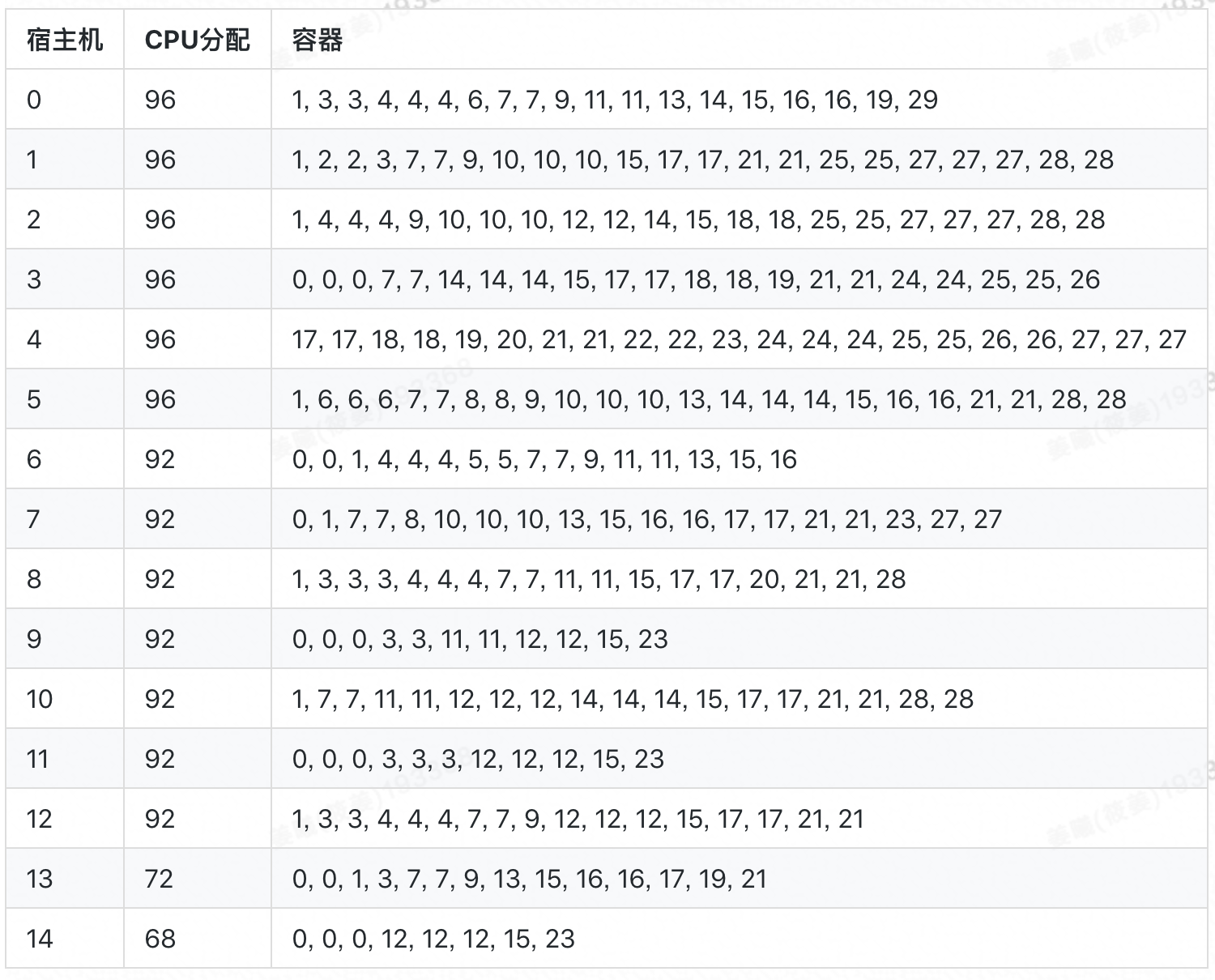
現實場景中，每個請求所處順序和容器數量僅在其到達 Sigma 時才揭曉，若採用 Best-Fit 進行動態排程，所得分配率為 70.83%，共啟用 20 臺宿主機，具體排布如下：

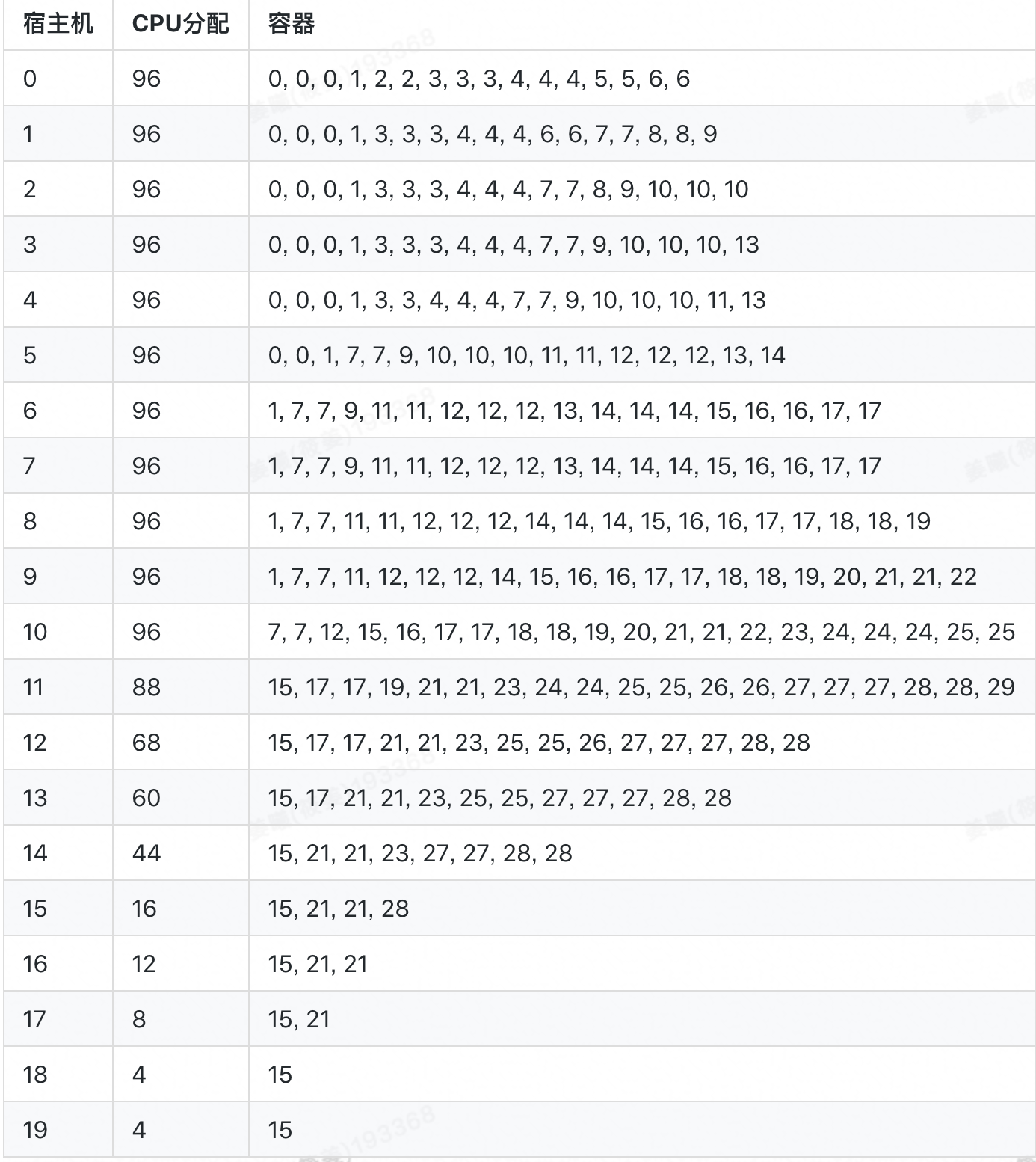
若採用 SwarmRL 學習所得策略進行動態分配，分配率為 94.44%，共啟用 15 臺宿主機，最終容器排布如下：

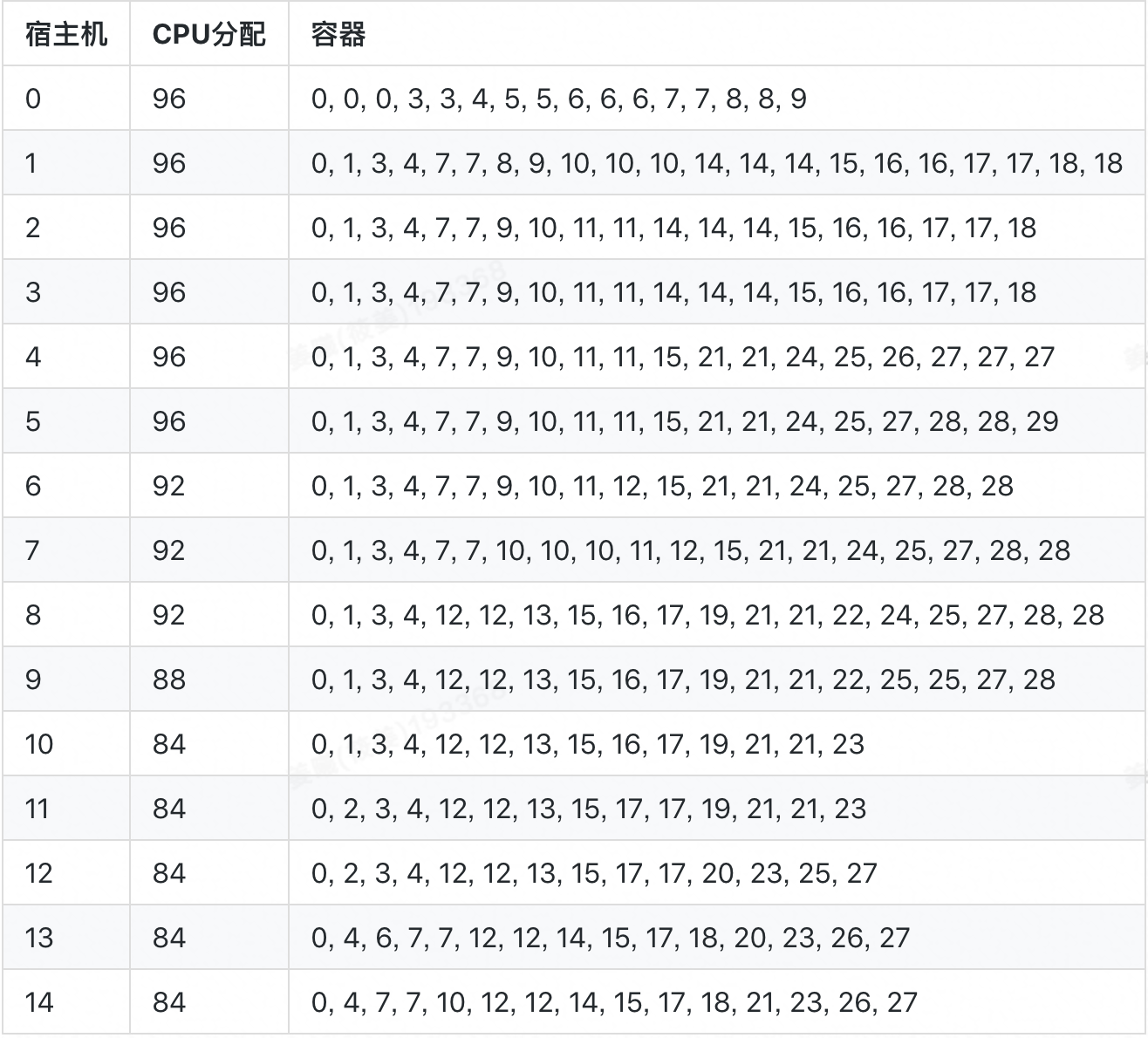
在該算例中，SwarmRL 學習所得策略的表現（94.44%）與“上帝視角”下最優排布的表現（上界）一致，明顯優於 Best-Fit 的表現（70.83%），改進幅度達 23.61%.

我們再隨機生成規模較大的請求資料：共計 3K 個請求，5K 個容器，其規格分佈如下圖，

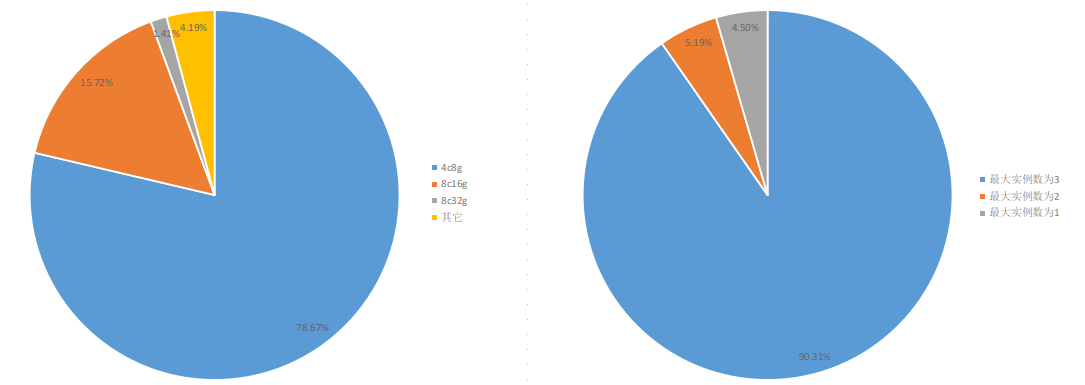
由於該場景下整數規劃模型的變數規模太大，已經無法在短時間內直接求取“上帝視角”的最優解。對比 Best-Fit （以及人肉策略），演算法所得新策略的效果如下：

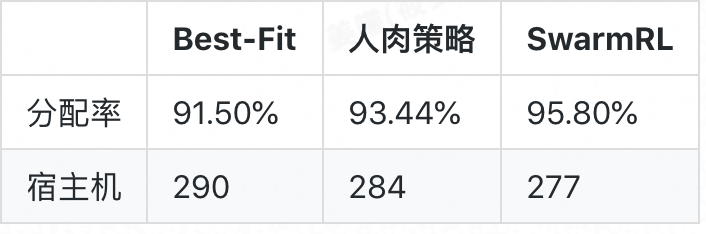
相對於 Best-Fit，新策略節約宿主機 13 臺（4.48%），分配率提升 4.30%；相對於人肉策略，新策略節約 7 臺（2.46%）宿主機，分配率改進 2.36%.

考慮到實際場景中應用請求到達順序的隨機性，我們隨機打亂請求生成多個不同的請求順序，再分別應用三個策略按不同的請求順序進行動態分配：

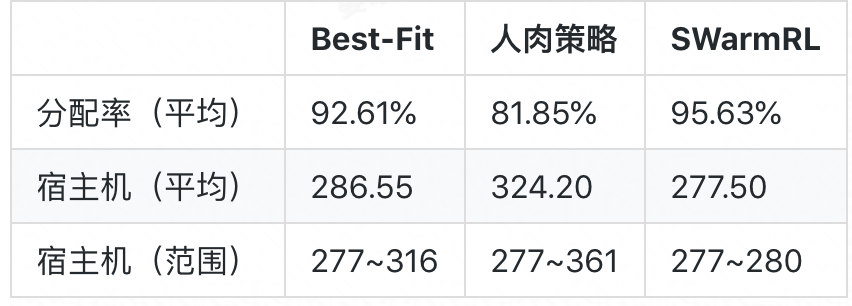
Best-Fit 在不同請求順序下宿主機數量的極差為 39 臺，相對人肉策略的 84 臺而言，表現相對穩定，其波動幅度約為人肉策略的一半；人肉策略的平均分配率低至 81.85%，對比原順序下的 93.44%，可見人肉策略的效能並不穩定，表現出較劇烈的波動。而學習所得新策略的表現則相當穩定，其宿主機數量的極差僅為 3 臺，波動幅度約為人肉策略的 30 分之一；新策略的分配率平均比人肉策略的分配率高 13.78%，比 Best-Fit 的高 3.02%.

5.總結與展望

從提升分配率、節省資源的角度來看，SwarmRL 演算法可以產生出優於常用（以及人肉）的策略，並且有著較為穩定的表現。演算法部署到線上環境後，公共資源池的分配率峰值與之前相比有了明顯的提升。

隨著 CPU share 和混部的鋪開，除分配率外，新的場景將涉及更多目標，比如打散、負載均衡等，這些目標甚至還有互相矛盾的地方，而 SwarmRL 的執行機制天然適合具有多個目標的策略優化問題，可以十分方便地在策略空間中構造 Pareto Front，因而，後續我們將繼續研究新場景下的線上排程策略問題，充分挖掘 SwarmRL 的潛力，進一步提升 Sigma 的排程能力。

參考文獻

• David Simchi-Levi, Xin Chen and Julien Bramel (2014). The Logic of Logistics: Theory, Algorithms, and Applications for Logistics Management (3rd ed). Springer
• Richard S. Sutton and Andrew G. Barto (2017). Reinforcement Learning: An Introduction. The MIT Press
• Hitoshi Iima, Yasuaki Kuroe and Kazuo Emoto (2011). Swarm reinforcement learning methods for problems with continuous state-action space, IEEE ICSMC
• Yossi Azar, Ilan R. Cohen, Amos Fiat and Alan Roytman (2016). Packing small vectors. SODA'16
• Yossi Azar, Ilan R. Cohen, Seny Kamara and Bruce Shepherd (2013). Tight bounds for online vector bin packing. STOC‘13