評價分類器的好壞
阿新 • • 發佈:2018-12-06
2018-12-06 17:05:27
這裡以二分類舉例,首先引入混淆矩陣的概念:
混淆矩陣是一個2×2的方陣,用於展示分類器預測的結果——真正(true positive),假負(false negative)、假正(false positive)及假負(false negative)
下面介紹一下各個評價指標:
正確率(Accuracy,ACC):正確率是最容易理解的,就是預測正確的樣本佔樣本總數的比例。
ACC = (TP + TN) / (TP + TN + FP + FN)
錯誤率(Error,ERR):錯誤率顯然就是1 - ACC,換句話說,就是預測錯誤的樣本佔樣本總數的比例。
ERR = (FP + FN) / (FP + FN + TP + TN)
查準率/精確率(Precision,PRE):精確率是指預測為正的樣本中到底有多少確實是正樣本。
PRE = TP / (TP + FP)
召回率(Recall,REC):召回率是指預測正確的正樣本數量佔總體正樣本數量的比例。
REC = TP / (TP + FN)
ROC曲線:
如正樣本有90個,負樣本有10個,直接把所有樣本分類為正樣本,得到識別率為90%,但這顯然是沒有意義的。因此就引入了ROC曲線的概念。
縱軸為真正類率(true positive rate,TPR),預測正確的正類佔總體正類的比例 :
TPR = TP / (TP + FN)
橫軸為真負類率(True Negative Rate,TNR),錯誤被預測為正類的樣本佔總體負樣本的比例 :
FPR = FP / (FP + TN)
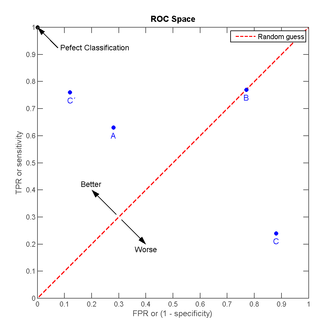
我們可以看出:左上角的點(TPR=1,FPR=0),為完美分類,也就是這個醫生醫術高明,診斷全對;點A(TPR>FPR),醫生A的判斷大體是正確的。中線上的點B(TPR=FPR),也就是醫生B全都是蒙的,蒙對一半,蒙錯一半;下半平面的點C(TPR<FPR),這個醫生說你有病,那麼你很可能沒有病,醫生C的話我們要反著聽,為真庸醫。
一個閾值,得到一個點。現在我們需要一個獨立於閾值的評價指標來衡量這個醫生的醫術如何,也就是遍歷所有的閾值,得到ROC曲線。還是一開始的那幅圖,假設如下就是某個醫生的診斷統計圖,直線代表閾值。我們遍歷所有的閾值,能夠在ROC平面上得到如下的ROC曲線。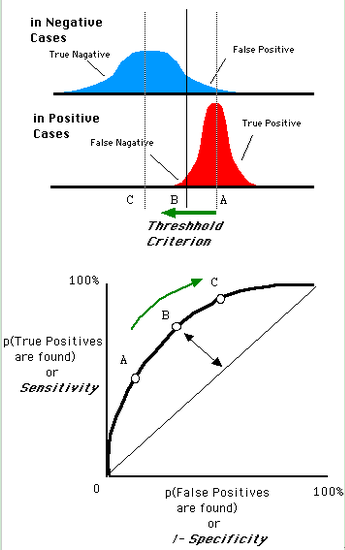
AUC :
AUC值為ROC曲線所覆蓋的區域面積,顯然,AUC越大,分類器分類效果越好。
- AUC = 1,是完美分類器,採用這個預測模型時,不管設定什麼閾值都能得出完美預測。絕大多數預測的場合,不存在完美分類器。
- 0.5 < AUC < 1,優於隨機猜測。這個分類器(模型)妥善設定閾值的話,能有預測價值。
- AUC = 0.5,跟隨機猜測一樣(例:丟銅板),模型沒有預測價值。
- AUC < 0.5,比隨機猜測還差;但只要總是反預測而行,就優於隨機猜測。
