關鍵：首先匯入的Excel資料為經緯度座標，所以僅設定空間座標系統WGS1984(暫不設定投影座標系)。然後用toolbox的project座標轉換，加上投影座標系，空間座標系轉換。
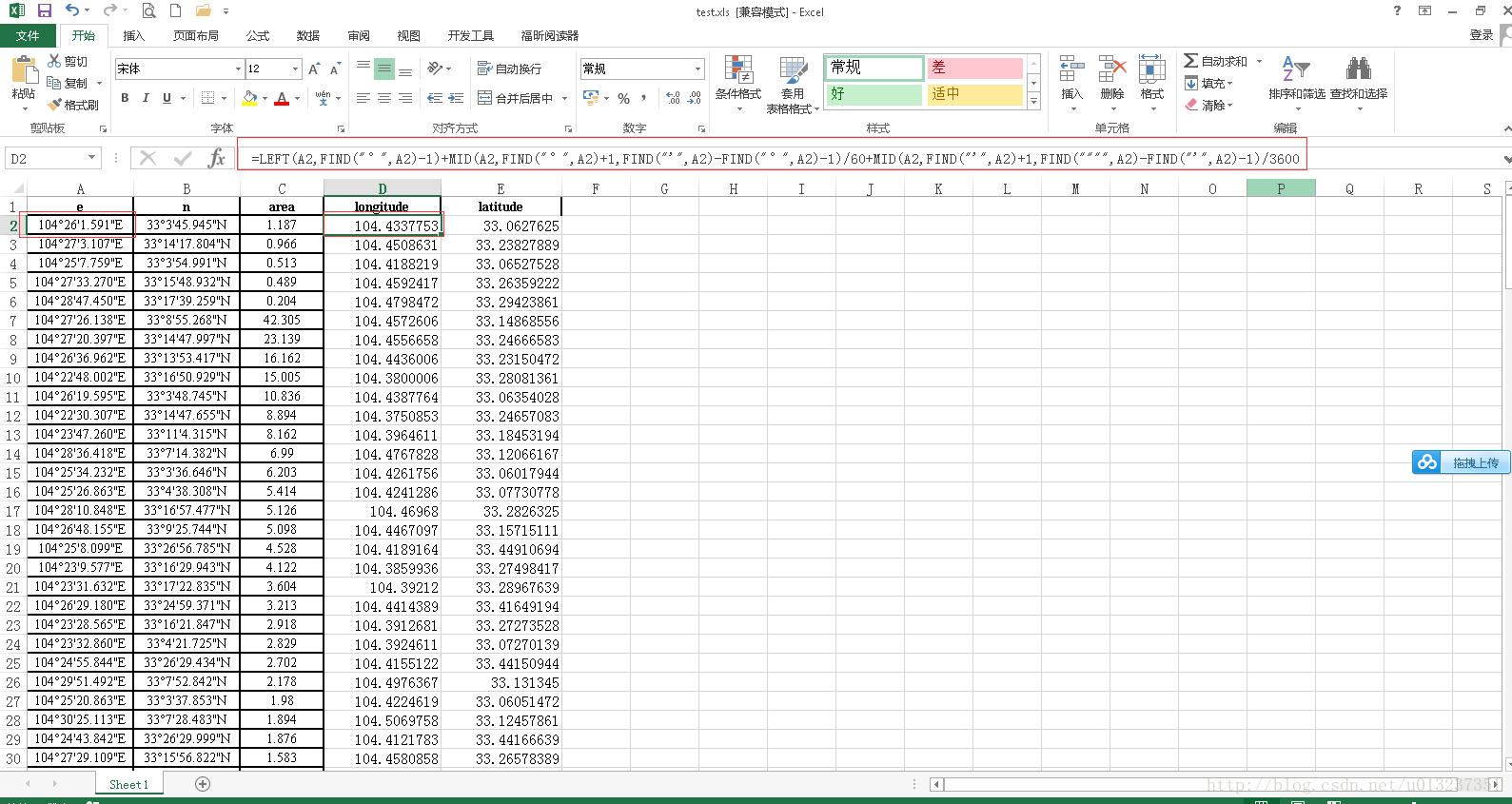
1.如果Excel為度分秒用Excel公式轉換成數值形式
公式：=LEFT(A2,FIND(“°”,A2)-1)+MID(A2,FIND(“°”,A2)+1,FIND(“’”,A2)-FIND(“°”,A2)-1)/60+MID(A2,FIND(“’”,A2)+1,FIND(“”“”,A2)-FIND(“’”,A2)-1)/3600

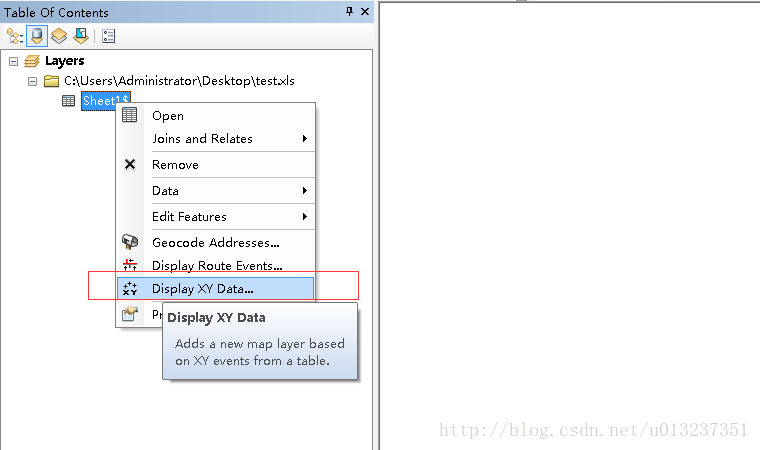
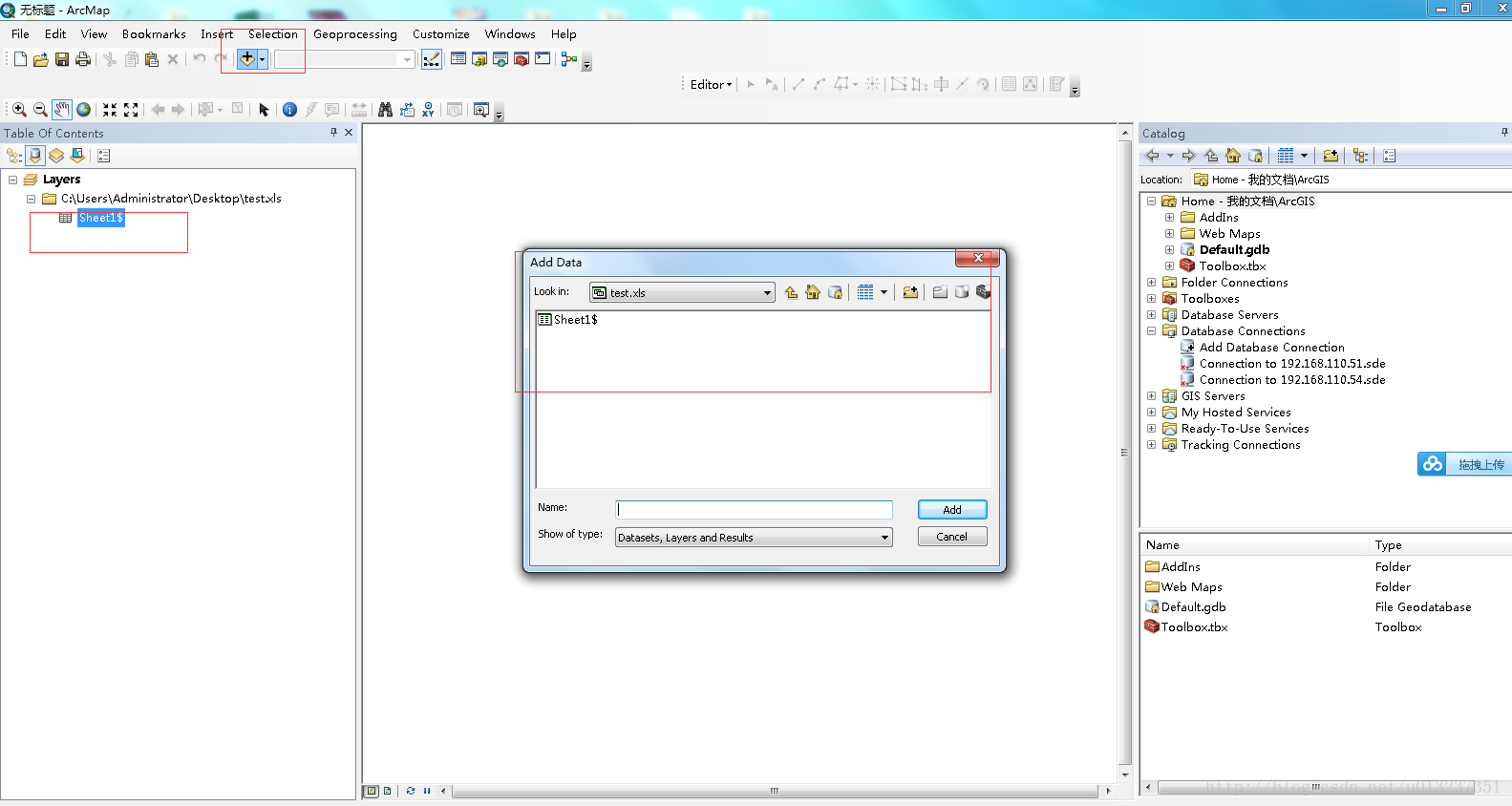
2.arcmap匯入Excel

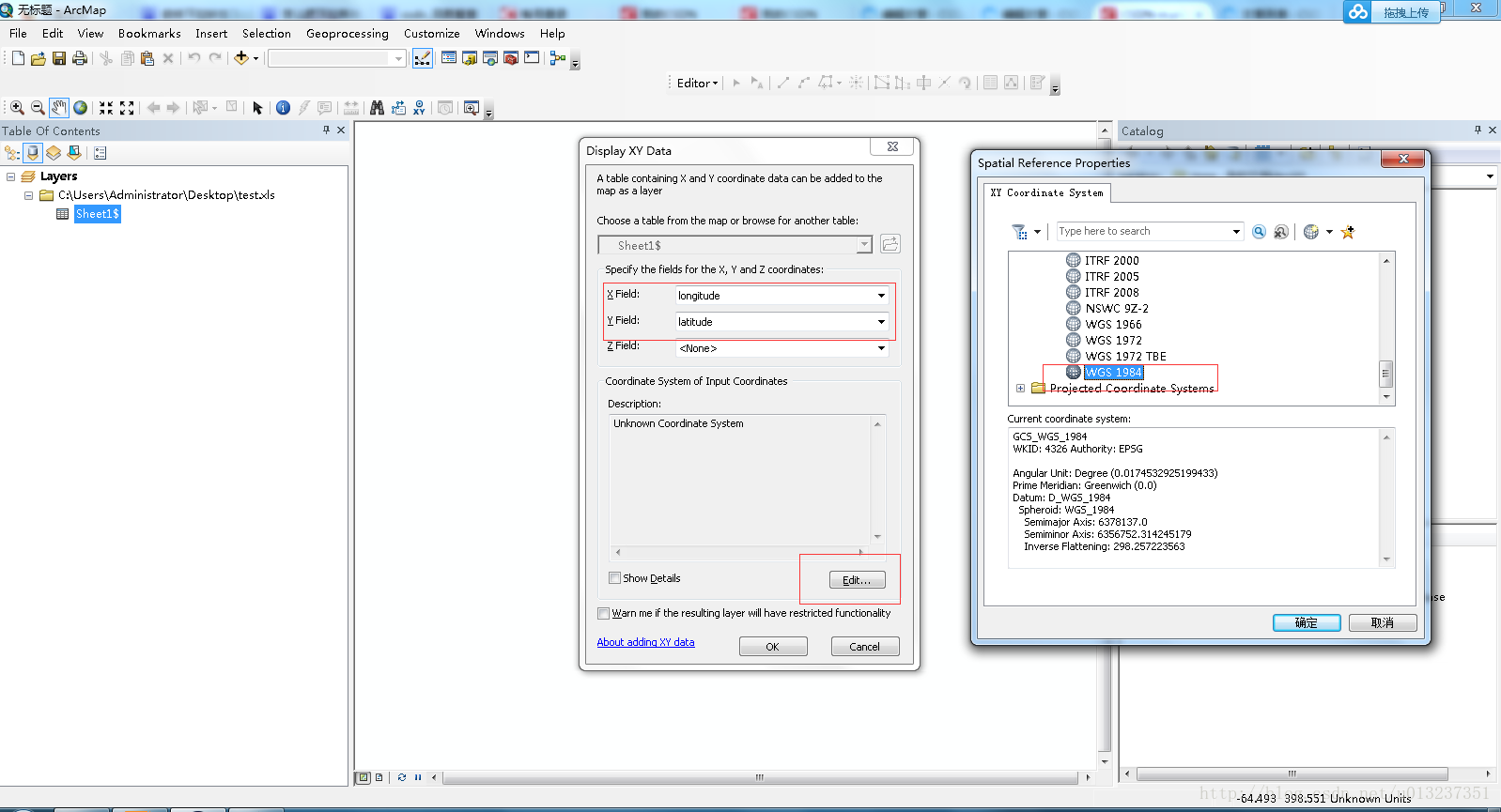
3.Display XY Data

4.Export data

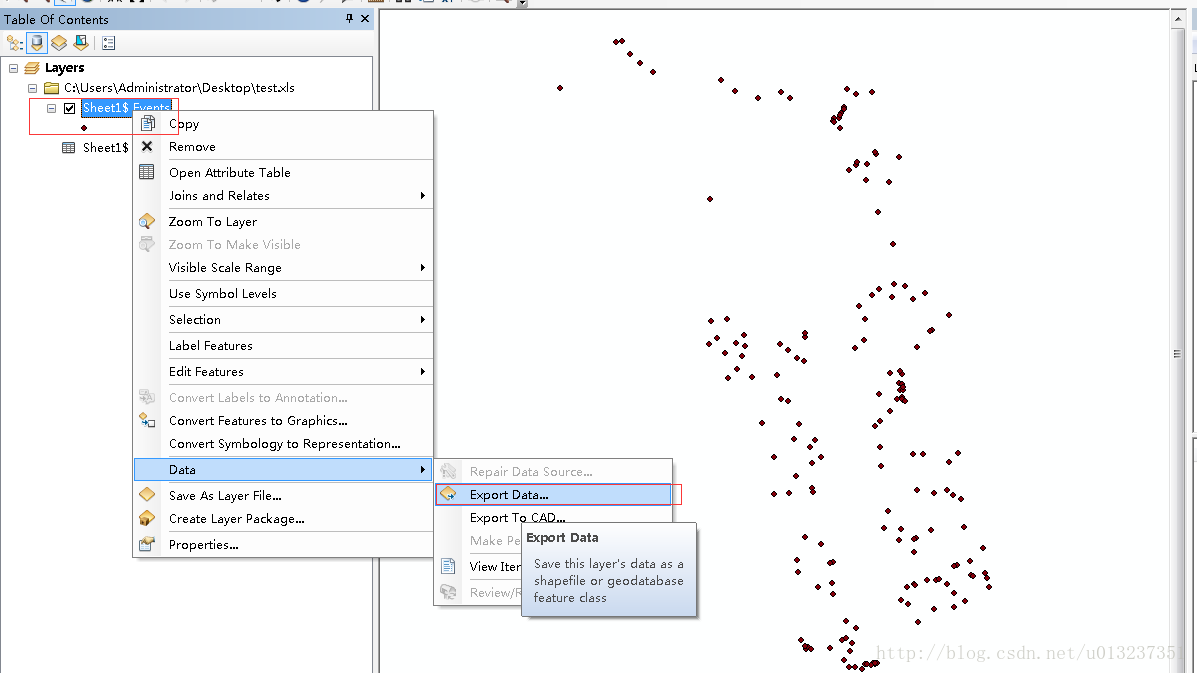
然後設定輸出路徑，ok
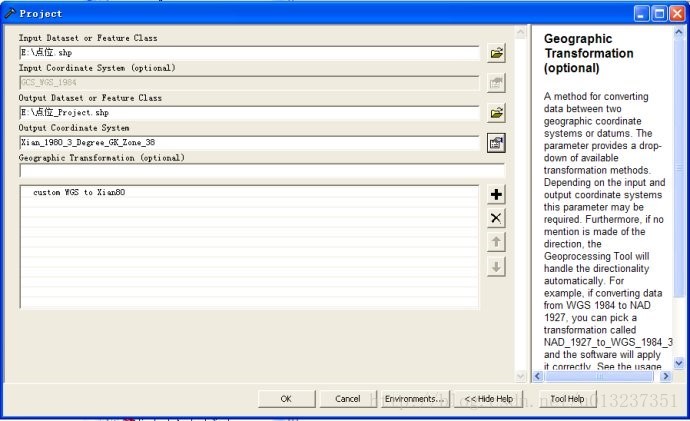
5.座標轉換
Data Management tools –>projections and Transformation
（由於預設地理座標轉換沒有WGS84轉西安，首先建立自定義的地理座標轉換）

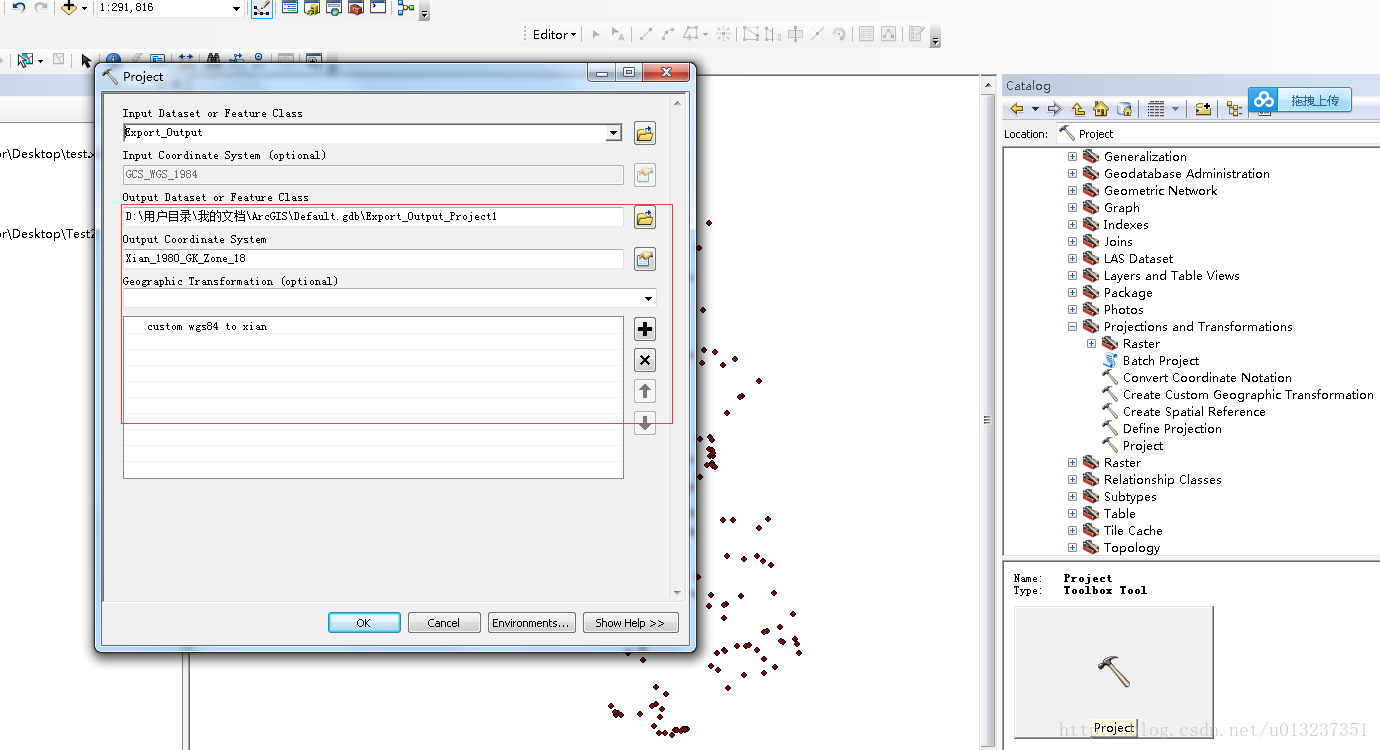
**注意**Geographic Transformation引數（有些座標系轉換的引數是不公開的，屬於涉密的內容，所以ArcGIS是沒有權利知道變換方法的。例如與Xian 80 有關的變換。）
如果不涉及到地理座標系變換的座標變換，這個引數完全不需要
例如：從 GCS_Xian_1980 進行投影變換，轉換為 Xian_1980_3_Degree_GK_CM_120E 投影座標系。 整過轉換中， 僅使用了高斯克呂格投影變換，沒有涉及到地理座標變換。
必須設定：
1.涉及到地理座標系變換的座標變換，並且ArcGIS 已知二者之間的變換方法，這個引數是必須的，在已知列表中做選擇或者自定義。（自定義見：情景3）
例如：從 GCS_Beijing_1954，轉換為 GCS_WGS_1984座標系。 轉換過程中涉及到地理座標系變換，也就是進行了橢球體變換。

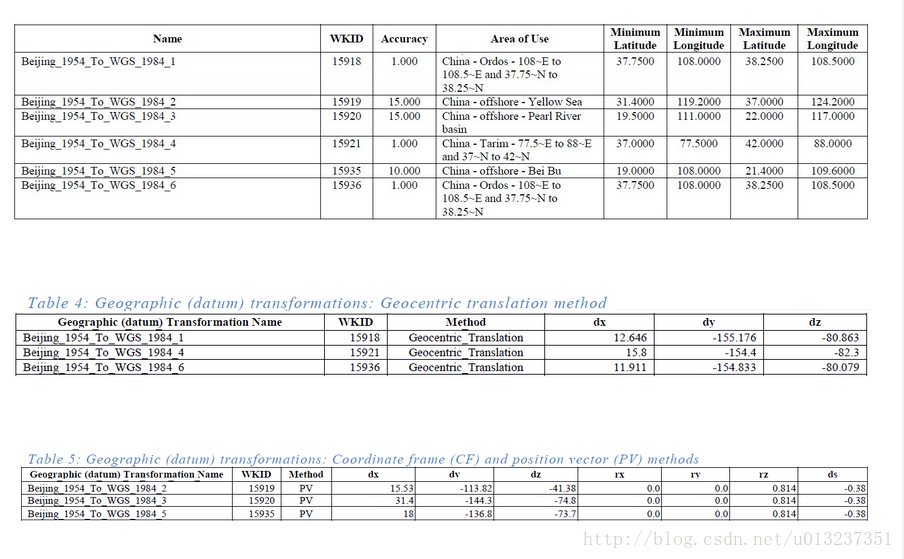
ArcGIS 中提供了6種已知轉換方法，可以根據適用範圍選擇之。Beijing_1954_To_WGS_1984
2.涉及到地理座標系變換的座標變換，並且ArcGIS 未知二者之間的變換方法，也就是ArcGIS沒有提供轉換方法，但是這個引數是必須的，需要自定義，這個引數前會亮綠燈，告訴使用者，必須要填寫。另外，上面情景2中，ArcGIS給出的方法，如果都不是自己需要的，也需要自定義。
例如：從GCS_Beijing_1954，轉換為GCS_Xian_1980座標系。
可建立一種變換方法，用於在兩個地理座標系或基準面之間對資料進行轉換。對於任何引數要求進行地理變換的工具，都可使用此工具的輸出作為變換方法。 Custom Geographic Transformation工具建立自定義地理座標轉換用於該引數
所有的自定義地理變換檔案都將儲存為副檔名為.gtf的檔案，並存儲在使用者Application Data資料夾下的ESRI\\ArcToolbox\CustomTransformations資料夾中。
ArcGIS 中提供地理變換方法主要有這幾種：Geocentric_Translation、Molodensky、Molodensky_Abridged、Position_Vector、Coordinate_Frame、Molodensky_Badekas、NADCON、HARN、NTV2、Longitude_Rotation、Unit_Change 和 Geographic_2D_Offset。可使用“建立自定義地理變換（Creat Custom Geographic Transformation）”工具來建立轉換方法。地理座標系包含了基於橢圓體的基準面，因此地理變換會更改基礎橢圓體。在基準面間進行變換的方法很多，這些方法具有不同的精度和範圍。
地理變換是針對地理座標系的，也就是經緯度座標進行轉換，如果輸入資料的座標系中還包含了平面座標系（投影），在使用 Project 工具的過程中會自動做相應的投影變換，轉到地理座標系，地理變換後，如果需要再轉為相應的投影座標系。
1）Geocentric_Translation
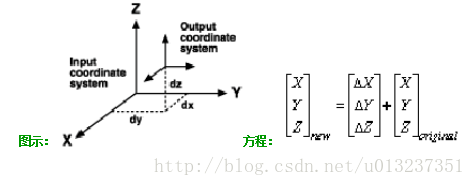
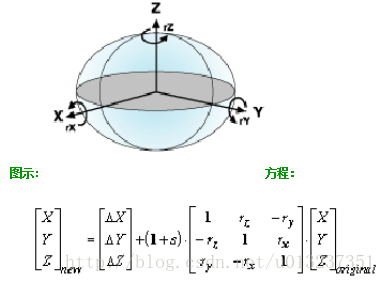
地心變換，也就是我們常說的三引數變換，是最簡單的基準面變換方法。地心變換在 XYZ 或 3D 直角座標系中對兩個基準面間的差異情況進行建模。定義一個基準面使其中心為 0,0,0。相距一定距離定義另一個基準面（dx,dy,dz 或 ΔX,ΔY,ΔZ，單位為米）。
圖示： 方程：

2）Coordinate Frame，Position Vector
這兩種方法是我們常說的七引數變換，或者布林沙模型。通過對三引數變換再增加四個引數可實現更復雜和精確的基準面變換。七個引數是指三個線性平移量 (dx,dy,dz)、繞各軸的三個角度旋轉值 (rx,ry,rz) 和一個比例尺因子。旋轉值以十進位制秒為單位給定，而比例尺因子採用百萬分率 (ppm)。
圖示： 方程：

為什麼七引數有上面兩種方法？其實可以認為是一種模型，只是不同的國家對旋轉量的正負號定義標準不同而已。
 座標框架旋轉變換（coordinate frame），美國和澳大利亞的定義，逆時針旋轉為正； 
位置向量變換（position vector），歐洲的定義，逆時針旋轉為負。
另外，莫洛金斯基–巴德卡斯（Molodensky_Badekas）方法是七引數方法的變型。它具有三個附加引數，用於定義旋轉點的 XYZ 原點。

3）Molodensky，Molodensky_Abridged
莫洛金斯基方法直接在兩種地理座標系之間轉換，實際上無需轉換到 XYZ 系統。莫洛金斯基方法需要三個平移量 (dx,dy,dz) 以及兩個旋轉橢球體的長半軸 (Δa) 和扁率 (Δf) 的差。 這種方法，相對用的少