在3.3節中，我們已經看到，弧度一致性是收緊網路的最自然的技術，受到了社群的高度關注。 儘管如此，這並不是收緊網路的唯一方法，早在70年代，一些作者提出的技術發現了比弧度一致性更多的不一致性。

3.4.1 Path Consistency 

Montanari提出路徑一致性是binary normalized網路中值對一致性的必要條件[95]。 粗略地說，如果對於一對變數（xi，xj）上的給定值對（vi，vj），存在從xi到xj的變數序列，這樣我們就無法找到從vi到vj處完成這些變數的值序列，並且滿足沿序列的所有二元約束，則（vi，vj）是不一致的。

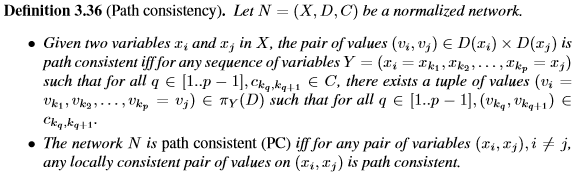
Montanari觀察到僅在長度為2的路徑上強制執行路徑一致性以獲得與路徑一致性相同的本地一致性水平是足夠的。

路徑一致性不會減少變數域，但會刪除值對。 結果，歸一化網路N的路徑一致性閉合不在Psol ND中。 我將PN2定義為PN的子集，其中網路被歸一化，並且僅通過新增或收緊二進位制約束使之與N不同。 N的路徑一致閉包PC（N）是PN2中所有路徑一致網路的並集（根據N）。在PN2中，可能存在幾個與PC（N）nogood-等效的網路 —— 因為具有相同方案的約束可以在非有效元組上不同，這不會改變本地不一致的例項化的集合。 然而，PC演算法可以擴充套件地表示修改約束，僅生成嵌入約束。 因此，如果我們考慮嵌入所有二進位制約束的網路，則關係是PN2上的部分順序，並且PC演算法保證收斂於PC（N）。

文獻中提出了幾種實現PC的演算法。 每次為弧一致性提出新技術時，它很快就會應用於路徑一致性。 可以看出PC1 [95,87]是蠻力AC1的路徑一致性計數器部分。 PC2是AC3對路徑一致性的擴充套件[87]。 PC3 [92]和PC4 [68]使用支援列表，如AC4，以達到最佳性。 PC5 [111]和PC6 [32]擴充套件了AC6。 PC7 [31]和PC8 [33]是PC6的簡化，在實踐中表現良好。 PC5 ++ [111]應用AC7的雙向性。 最後，PC2001 [126,25]擴充套件了AC2001。

路徑一致性的一個缺點是強制執行它會產生CN中沒有的其他約束（參見例3.37）。 此外，即使約束c（xi，x j）已經在CN中，PC的改進也可以強制改變其語義並且可以擴充套件地表示這個新約束，而它是作為函式給出的。

我們可以注意到的最後一點是，雖然通常在二進位制規範化網路中考慮路徑一致性，但定義3.36中沒有任何內容阻止其在非二進位制規範化網路上的使用。 非二進位制約束只是被忽略了。

3.4.2 k-Consistencies

在Montanari的論文發表幾年後，Freuder將區域性一致性的概念從AC強化到了一整個類的一致性，稱為k-一致性[53,54]。

k元一致性：對|Y|=k-1的變數集，第k個變數能找到至少一個值，使它和變數集中的其他變數共同組成一個解。

3-consistency和(2-)path consistency是不等價的。正如Dechter [46]所觀察到的，即使3-consistency與（2-）路徑一致性具有很強的相似性，它也不是等價的。 實際上，3-一致性確保長度為2的任何例項化都可以擴充套件到涉及任何第三變數的例項化而不違反任何約束，而（2-）路徑一致性僅保證不違反二進位制約束。

k-consistency確保每次我們有一個大小為k-1的本地一致的例項化時，我們可以始終將它擴充套件到任何第k個變數。 那麼，問題是“如何構建大小為k-1的本地一致例項化？”。 強k-一致性是保證網路在1≤j≤k時j-一致的性質。 因此，我們可以從頭開始構建一個大小為k的本地一致的例項，而不需要任何回溯。

Freuderand Cooper在[53,37]中提出的演算法都達到了一個不是強k-一致閉包的點。 它們使所有約束（最多為arity k-1）儘可能明確。 例如，如果一對值（（xi，v i），（xj，v j））是路徑不一致的，它們會在{xi，x j}的每個超集Y上建立一個約束，其中| Y | <k，並且該約束禁止在Y上的所有元組τ，其中τ[（xi，x j）] =（vi，v j）。 Cooper表明他的演算法執行在中，這是強k-一致性的最佳時間複雜度。 Cooper提出的演算法需要O（nkdk）空間。 強k-一致性的最佳空間複雜度是，因為我們必須儲存k-consistency的每個約束k-1的約束，每次大小為k-1的例項化不延伸到第k個變數。

我在3.2節中說過，我們可以在網路上執行的最大簡化量是達到一個全球一致的網路，也就是說，所有本地一致的例項都可以擴充套件到解決方案的網路。 強n-一致性保證了這一點。

在任意網路上實現全域性一致性太耗費空間（在O（nn-1dn-1）中）。 Freuder給出了相關超圖的條件，其中強k-一致性（k <n）足以允許無回溯搜尋[54]。在[47]中，Dechter和Pearl開發了自適應一致性（AdC），這是一種受動態程式設計啟發的技術。給定變數的總排序，AdC根據與xi共享約束的變數的數量以及在排序中在其之前的變數的數量來調整對每個變數xi強制執行的k-一致性的級別。獲得的網路保證無回溯搜尋。 （見第7章）在[55]中，Freuder提出了（i，j） - 一致性，k-一致性的推廣，其中我們不保證大小為k-1的例項可以擴充套件到大小為k的例項，但是例項化大小我可以擴充套件到j個附加變數。 k-一致性是（k-1,1）一致性。由於k-一致性的主要缺點是它們需要儲存大小為k-1的所有禁止例項的巨大空間，我們可以通過將i設定為（i，j） - 一致性中的小值來設計需要較少空間的區域性一致性。

3.4.3 Montanari’s Decomposability and Minimality

3.4.3 Montanari的可分解性和極簡性

蒙塔納裡描述了可以在多項式空間中全域性一致的網路。 這些是一組解決方案是可分解關係的網路[95]，在[46]中也稱為二進位制可分解關係。

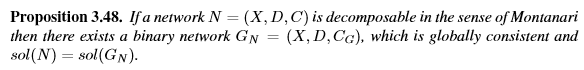
Montanari的可分解性強於通常所說的“可分解約束”。 （更多詳細資訊，請參見[63]或第3.8.2節。）示例3.47顯示，不是因為網路是二進位制的，它在Montanari意義上是可分解的。 對於二進位制網路，Montanari提出了最小網路的概念，這是用於全域性一致性的最佳近似二進位制網路。 因此，這是收緊二進位制網路的另一種技術。

定義3.49（Minimalnetwork） 給定二進位制網路N =（X，D，C），N的最小網路是二進位制歸一化並且嵌入在D網路MN =（X，D，CM）中，使得長度2的任何本地一致的例項化是全域性一致的並且sol （MN）= sol（N）。

推論3.50  給定二進位制網路N，如果sol（N）在Montanari意義上是可分解的，則最小網路MN是全域性一致的。

二進位制網路上的極小性可以被認為是一種本地一致性。 但區域性一致性通常指的是多項式強制執行的屬性。 構建最小網路顯然是難以處理的，因為一旦我們擁有最小網路，就可以確定原始網路的一致性（通過檢查任何約束的空虛）。 建立最小網路的問題被蒙塔納裡稱為“核心問題”。 這導致了一些混亂，因為有時候認為如果網路很小，生成解是多項式的。 Dechter通過以下方式部分地解決了歧義：

“然而，現在仍然不清楚是否生成單一最小網路解決方案很難，即使經驗經驗表明它通常很容易。 儘管如此，我們確實推測從最小網路生成單一解決方案很難......“

我們可以多說一點。

證明。 除非ΠP2=ΣP2 [29]，否則已知條款蘊涵問題是不可編譯的。 在[38]中，Cros將子句蘊涵問題簡化為二進位制網路N中部分例項化的全域性一致性問題的可編譯性。如果在最小網路中構建解決方案是無回溯的，那麼回答部分例項化是否全域性一致將是多項式的。 此外，最小網路的大小為O（n2d2），這是N大小的多項式。因此，部分例項化的一致性問題是可編譯的，並且條款蘊涵也是如此。

3.4.4 Consistencies Based on Constraints基於約束的一致性

到目前為止我研究的所有一致性（弧一致性除外）都是變數的部分例項化的特性。 它們沒有考慮網路拓撲，即哪些變數集由約束連結而哪些不是。 這是約束傳播的限制，它在網路中的任何地方建立新的約束。 如果我們想要在無回溯條件下連結一致性級別和超圖結構，這也是對非二進位制網路的限制。 在本節中，我將注意力限制在嵌入式網路中，因為我提出的所有工作都使用了此限制。

Janssenetal提出了基於變數的約束的第一個區域性一致性[72]。 它適用於關係資料庫的工作[7]。

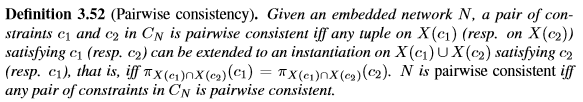
成對一致性：任取X(c1)的滿足c1的元組，都可以擴充套件到X(c1) U X(c2)，滿足c2。

Janssenetal在[72]中表明，在網路的雙重編碼中，對於2-一致性來說，它具有等效性，而且變數代表了原始網路的約束[48]。

在資料庫環境中，Gyssens提出了k-一致性，成對一致性的直接擴充套件，我們一次考慮k個約束而不是兩個[67]。 J'egou將這一概念應用於約束網路[73]。

k-一致性是k-逆一致性的基於約束的對應物（參見第3.5節）。 強制執行k-一致性不會改變相關的超圖。 它只是改變現有的約束。 在[74]中，J'egoup提出了變數和約束之間的另一個二元性。 他呈現出超k一致性。 這是基於約束的k-一致性對應物。

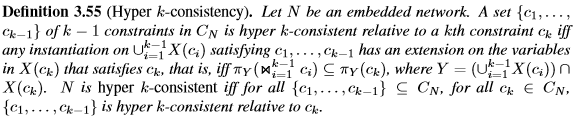
成對一致性是2向一致性和超2一致性。 根據定義3.55，J'egou描述了網路的一些充分條件是一致的。 這些條件將網路的超k一致性水平與其超圖的寬度聯絡起來。 然而，超k-一致性繼承了k-一致性的缺點之一，因為強制性一致性會增加新的約束，這些變數在原始網路中沒有連結。 Dechter和van Beek提出了一種新的區域性一致性形式，它與網路中已經存在的約束方案相比，超過了k-一致性。 他們將這些新的一致性稱為關係一致性[49]。

設N是嵌入式網路。 CN中的約束c相對於變數Y subsetX（c）的子集是關係一致的，如果Y上的任何區域性一致的例項化對X（c）上的元組的擴充套件滿足c。 如果相對於X（c）的每個子集Y具有相對弧度一致，則c是關係弧一致的。 如果CN中的每個約束是關係一致的，則N是關係弧一致的。

關係弧一致性的一個優點是強制它不會在原始網路中未連結的變數之間建立約束。但是，它會在原始約束的方案的子集上建立子約束，這對於大型約束可能是禁止的，因為它最多可以為約束c建立2 | X（c）| 個子約束。

關係m-一致性具有與超k-一致性相同的缺點，因為它可以對m個約束之一中涉及的任何變數子集建立新約束。 Dechter和van Bee提出了關係m-一致性的有界版本，可以解決時空爆炸問題。

關係弧一致性對應於強關係（n，1） - 一致性和關係m-一致性對應於強關係（n，m） - 一致性。 廣義弧一致性是關係（1,1）一致性。 關係（1，m） - 一致性是基於域的一致性，因此，不要修改約束集。

與強k-一致性的情況一樣，強制關係（i，m）一致性的演算法可以根據它們產生新約束的順序收斂到不同的網路。

Dechter和van Beek提出了一種強制執行關係（i，m）一致性的演算法。 它的複雜性在i·m中是指數級的。 他們還提出了一種自適應關係一致性演算法。 它受到自適應一致性的啟發（參見第7章），並應用適當級別的關係一致性來保證對給定變數排序的解決方案進行無回溯搜尋。

沃爾什對關係一致性與k-一致性，k-逆一致性和廣義弧一致性進行了廣泛的理論比較[123]。