參考：https://www.cnblogs.com/cymwill/p/7823148.html

Numpy matrices必須是2維的,但是 numpy arrays (ndarrays) 可以是多維的（1D，2D，3D····ND）. Matrix是Array的一個小的分支，包含於Array。所以matrix 擁有array的所有特性。

1.mat.getA()：將自身矩陣變數轉化為ndarray型別的變數。等價於np.asarray(self)

2.mat.getA1()：將自身矩陣變換為一維的ndarray型別。等價於np.asarray(self).ravel()

3.mat.getH()：返回自身(如果是複數矩陣)對偶轉置矩陣，如果為實數矩陣，則等價於np.transpose(self)

4.mat.getI()：返回可逆矩陣的逆。

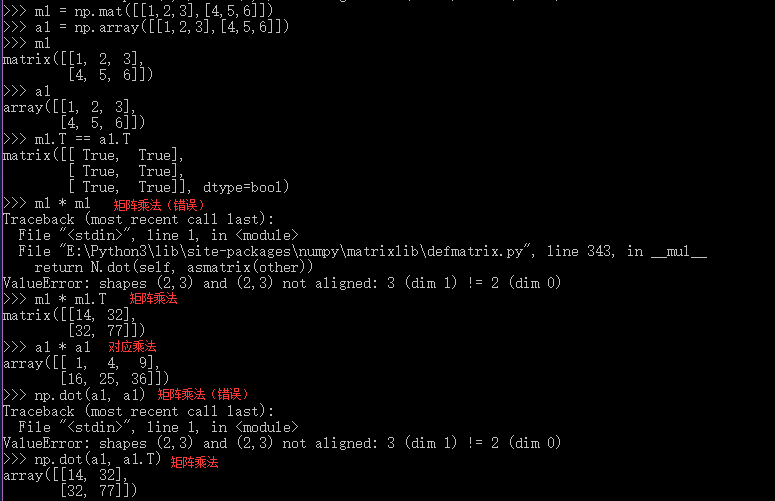
在numpy中matrix的主要優勢是：相對簡單的乘法運算子號。例如，a和b是兩個matrices，那麼a*b，就是矩陣積。而不用np.dot()。如：

import numpy as np

a=np.mat('4 3; 2 1')
b=np.mat('1 2; 3 4')
print(a)
# [[4 3]
#  [2 1]]
print(b)
# [[1 2]
#  [3 4]]
print(a*b)
# [[13 20]
#  [ 5  8]]
 

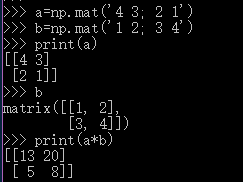
 matrix 和 array 都可以通過objects後面加.T 得到其轉置。但是 matrix objects 還可以在後面加 .H f得到共軛矩陣, 加 .I 得到逆矩陣。

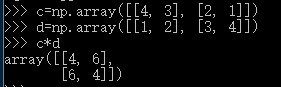
相反的是在numpy裡面arrays遵從逐個元素的運算，所以對於array：c 和d的c*d運算相當於matlab裡面的c.*d運算。

c=np.array([[4, 3], [2, 1]])
d=np.array([[1, 2], [3, 4]])
print(c*d)
# [[4 6]
#  [6 4]]
 

而矩陣相乘，則需要numpy裡面的dot命令 :

print(np.dot(c,d))
# [[13 20]
#  [ 5  8]]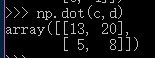

 但是python中矩陣沒有MATLAB中的.*這個性質，對於matrix對應乘法得用np.multiply()

>>> np.multiply(a,b)
matrix([[ 4,  6],
                [6,  4]])   

當然 ** 運算子的作用也不一樣 ：

print(a**2)  #矩陣乘法
# [[22 15]
#  [10  7]]
print(c**2)  #對應乘法
# [[16  9]
#  [ 4  1]]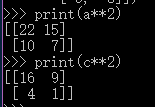

問題就出來了，如果一個程式裡面既有matrix 又有array，會讓人腦袋大。但是如果只用array，你不僅可以實現matrix所有的功能，還減少了程式設計和閱讀的麻煩。

當然你可以通過下面的兩條命令輕鬆的實現兩者之間的轉換：np.asmatrix和np.asarray

對我來說，numpy 中的array與numpy中的matrix，matlab中的matrix的最大的不同是，在做歸約運算時，array的維數會發生變化，但matrix總是保持為2維。例如下面求平均值的運算

>>> m = np.mat([[1,2],[2,3]])
>>> m
matrix([[1, 2],
        [2, 3]])
>>> mm = m.mean(1)
>>> mm
matrix([[ 1.5],
        [ 2.5]])
>>> mm.shape
(2, 1)
>>> m - mm
matrix([[-0.5,  0.5],
        [-0.5,  0.5]])

對array 來說

>>> a = np.array([[1,2],[2,3]])
>>> a
array([[1, 2],
       [2, 3]])
>>> am = a.mean(1)
>>> am.shape
(2,)
>>> am
array([ 1.5,  2.5])
>>> a - am #wrong
array([[-0.5, -0.5],
       [ 0.5,  0.5]])
>>> a - am[:, np.newaxis]  #right
array([[-0.5,  0.5],
       [-0.5,  0.5]])