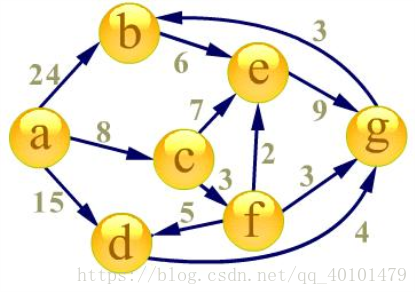
圖論 最短路 SPFA + 前向星存邊
阿新 • • 發佈:2018-12-08
- 介紹
==== - SPFA
SPFA已死
SPFA是基於Bellman - Ford的一種賊快的演算法, 用佇列來實現。
通常用於求含負權邊的單源最短路徑,以及判負權環。
SPFA 最壞情況下複雜度和樸素 Bellman-Ford 相同,為 O(VE)。
(參考百度百科)
毒瘤資料免談
- 前向星
一個數據結構,裡面的成員可以儲存起點,終點和權值。
要有一個數組維護每點連出去的邊的起點。
1.鏈式前向星構造
這裡我們使用的是鏈式前向星,用結構體儲存每一條邊:
struct Edge
{
//其實還可以記錄這條邊的起點,但這題沒必要 再開個first陣列
first[i] 表示以i為起點的第一條邊
2.加邊
first[i]其實就是以i為起點的邊所組成的連結串列的第一個元素。
每次加邊,我們讓first[i]這條邊指向要加的邊,再將所加的邊更新為first[i]。
因此,我們每次遍歷是倒著遍歷的:
void AddEdge(int begin, int end, int w)
{
len++; //第len條邊
e[len] = Edge{first[begin] 3.遍歷
從第一條邊開始,e[i].[next] 即為下一條邊的編號,從而遍歷以s為起點的所有邊,當邊的編號為0時即跳出迴圈
for (int i = first[s]; i; i = e[i].next)
- 演算法
======
思想:
我們先將起點入隊, 將所有與起點相連的點進行鬆弛操作。
如果鬆弛成功的點不在佇列裡,就把它進隊。
最後隊空即結束。
上程式碼:
#include 撒花結束