5在1e9+9下有二次剩餘，那麼fib的通項公式就有用了。

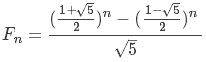　　已知Fn，求n。注意到[(1+√5)/2]·[(1-√5)/2]=-1，於是換元，設t=[(1+√5)/2]ⁿ，原式變為√5·Fn=t-(-1)ⁿ·t^-1。同乘t並移項，可得t²-√5·Fn·t-(-1)ⁿ=0。討論n的奇偶性，BSGS求二次剩餘大力解方程即可。用BSGS求二次剩餘是非常簡單的，求出其以原根為底的離散對數即可。

　　注意二次剩餘有正負兩解，但似乎代進去正根（即√g^k=g^k/2）就行了，不太明白。以及題目要求最小解，BSGS的時候注意順序。還有BSGS不一定有解，我也不知道我在BSGS裡面assert了半天是在幹啥。調了一年慘炸了。

#include<iostream> 
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<map>
#include<cassert>
using namespace std;
#define ll long long
#define P 1000000009
char getc(){char c=getchar();while ((c<'A'||c>'
 
Z')&&(c<'a'||c>'z')&&(c<'0'||c>'9')) c=getchar();return c;}
int gcd(int n,int m){return m==0?n:gcd(m,n%m);}
int read()
{
    int x=0,f=1;char c=getchar();
    while (c<'0'||c>'9') {if (c=='-') f=-1;c=getchar();}
    while (c>='0'&&c<='9') x=(x<<1)+(x<<3
 
)+(c^48),c=getchar();
    return x*f;
}
int n,b,g,v,ans=P;
map<int,int> f;
int ksm(int a,int k)
{
    int s=1;
    for (;k;k>>=1,a=1ll*a*a%P) if (k&1) s=1ll*s*a%P;
    return s;
}
int inv(int a){return ksm(a,P-2);}
int BSGS(int g,int k)
{
    f.clear();
    int block=sqrt(P),t=ksm(g,block),x=1,ans=-1;g=inv(g);
    for (int i=0;i<block;i++)
    {
        if (f.find(1ll*x*k%P)==f.end()) f[1ll*x*k%P]=i;
        x=1ll*x*g%P;
    }
    x=1;
    for (int i=0;i<P;i+=block)
    {
        if (f.find(x)!=f.end()) {ans=f[x]+i;break;}
        x=1ll*x*t%P;
    }
    return ans;
}
int SQRT(int n)
{
    int k=BSGS(g,n);
    if (k==-1||k&1) return -1;
    return ksm(g,k>>1);
}
void solve(int c,int op,int op2)
{
    int delta=SQRT(((1ll*b*b-4ll*c)%P+P)%P);
    if (delta==-1) return;
    delta=(P+op2*delta)%P;
    int ans1=1ll*((delta-b)%P+P)%P*inv(2)%P,ans2=1ll*((-delta-b)%P+P)*inv(2)%P;
    ans1=BSGS(v,ans1),ans2=BSGS(v,ans2);
    if ((ans1&1)==op&&ans1>0) ans=min(ans,ans1);
    if ((ans2&1)==op&&ans2>0) ans=min(ans,ans2);
}
int fib(int n)
{
    struct matrix
    {
        int n,a[2][2];
          matrix operator *(const matrix&b) const
           {
            matrix c;c.n=n;memset(c.a,0,sizeof(c.a));
            for (int i=0;i<n;i++)
                for (int j=0;j<2;j++)
                    for (int k=0;k<2;k++)
                    c.a[i][j]=(c.a[i][j]+1ll*a[i][k]*b.a[k][j])%P;
            return c;
        }
    }f,a;    
    f.n=1;f.a[0][0]=0,f.a[0][1]=1;
    a.n=2;a.a[0][0]=0,a.a[0][1]=a.a[1][0]=a.a[1][1]=1;
    for (;n;n>>=1,a=a*a) if (n&1) f=f*a;
    return f.a[0][0];
}
void work(int sqrt5)
{
    b=(P-1ll*sqrt5*n%P)%P;
    v=1ll*(sqrt5+1)*inv(2)%P;
    solve(P-1,0,1),solve(1,1,1);
    //solve(P-1,0,-1),solve(1,1,-1);
}
int main()
{
#ifndef ONLINE_JUDGE
    freopen("bzoj5104.in","r",stdin);
    freopen("bzoj5104.out","w",stdout);
    const char LL[]="%I64d\n";
#else
    const char LL[]="%lld\n";
#endif
    /*for (int i=2;;i++)
    {
        bool flag=1;
        for (int j=2;j*j<P;j++)
        if ((P-1)%j==0)
        {
            if (ksm(i,j)==1) {flag=0;break;}
            if (ksm(i,(P-1)/j)==1) {flag=0;break;}
        }
        if (flag) {g=i;break;}
    }*/
    g=13;
    n=read();
    work(SQRT(5));//,work(P-SQRT(5));
    if (ans==P) cout<<-1;else assert(fib(ans)==n),cout<<ans;
    return 0;
}