【劍指offer】陣列中的逆序對(校正書上錯誤)【歸併排序】
阿新 • • 發佈:2018-12-09
題目描述
在陣列中的兩個數字,如果前面一個數字大於後面的數字,則這兩個數字組成一個逆序對。輸入一個數組,求出這個陣列中的逆序對的總數P。並將P對1000000007取模的結果輸出。 即輸出P%1000000007
題目保證輸入的陣列中沒有的相同的數字
資料範圍:
對於%50的資料,size<=10^4
對於%75的資料,size<=10^5
對於%100的資料,size<=2*10^5
演算法思路
歸併排序可以用來尋找逆序對,時間複雜度為O(logN)
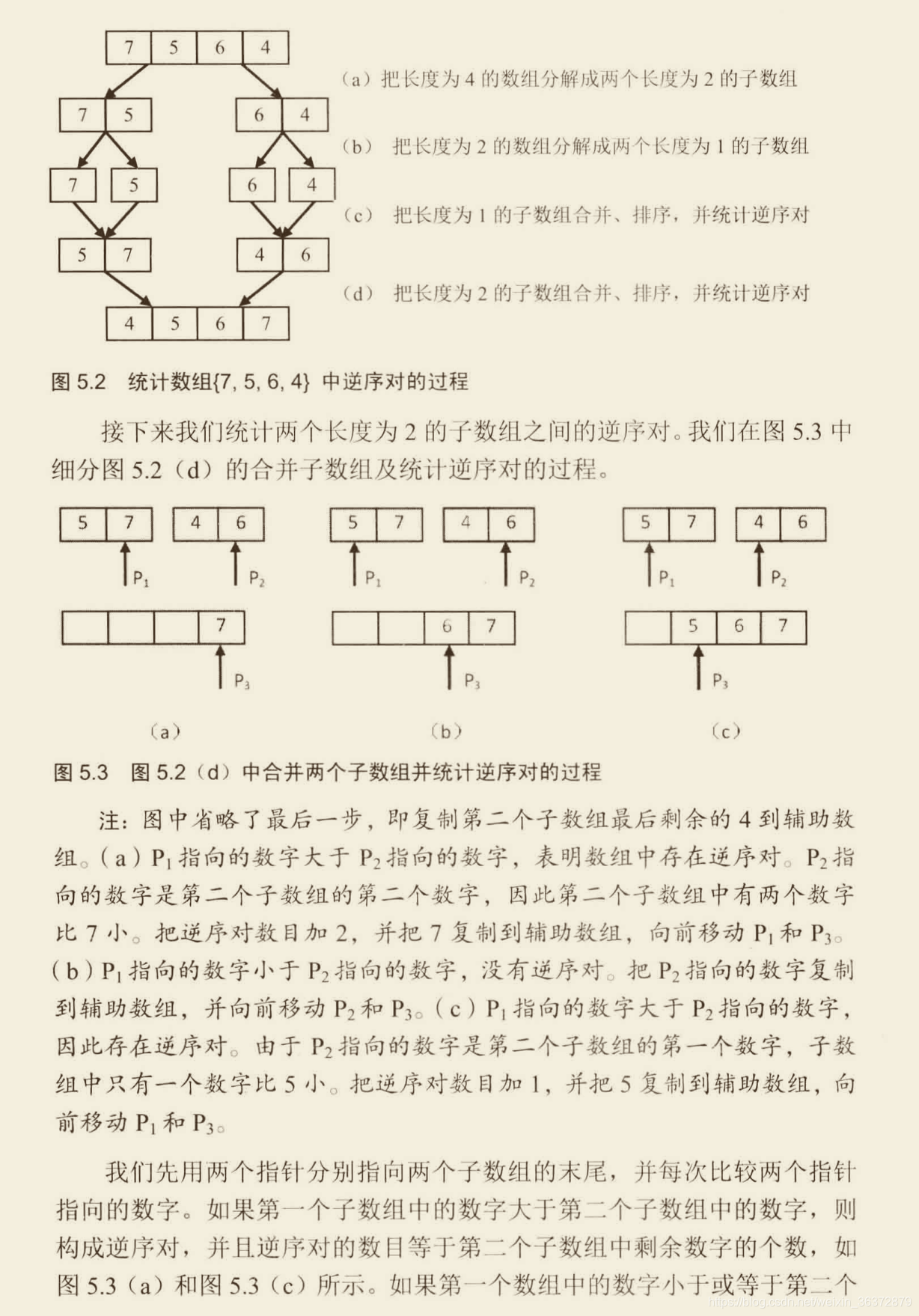
書中程式碼的錯誤:
按照書上的演算法,可以寫出如下程式碼:
class Solution: 輸出:
0 3 [7, 5, 6, 4] [7, 5, 6, 4]
0 1 [7, 5, 6, 4] [7, 5, 6, 4]
0 0 [7, 5, 6, 4] [7, 5, 6, 4]
1 1 [7, 5, 6, 4] [7, 5, 6, 4]
0 1 [7, 5, 6, 4] [5, 7, 6, 4]
2 3 [7, 5, 6, 4] [5, 7, 6, 4]
2 2 [7, 5, 6, 4] [5, 7, 6, 4]
3 3 [7, 5, 6, 4] [5, 7, 6, 4]
2 3 [7, 5, 6, 4] [5, 7, 4, 6]
0 3 [7, 5, 6, 4] [6, 4, 7, 5]
6
從輸出可以看到,並沒有輸出正確的結果,也沒有排序,原因是data陣列並沒排序好,copy陣列是根據data陣列排序的,但是data陣列並沒有在遞迴結束前有序。比如[7, 5, 6, 4] [5, 7, 4, 6],5比4大的時候,將5作為copy的最後一個元素。最後輸出[6, 4, 7, 5]。
正確的解法(超時)
class Solution:
def RecursionCount(self, data, copy, start, end):
print(start, end, data, copy)
if start >= end:
copy[start] = data[start]
return 0
count = 0
length = int((end - start) / 2)
leftCount = self.RecursionCount(data, copy, start, start + length)
rightCount = self.RecursionCount(data, copy, start + length + 1, end)
data = copy[:] #排序好之後,data要拷貝copy,才能保證data兩邊是排好序的。
i, j = start + length, end
copyIndex = end
while i >= start and j >= start + length + 1:
if data[i] > data[j]:
copy[copyIndex] = data[i]
copyIndex -= 1
i -= 1
count += (j - start - length)
else:
copy[copyIndex] = data[j]
copyIndex -= 1
j -= 1
#比較之後,可能有一邊沒遍歷完,copy可能沒被全部填滿,需要繼續填充copy
while i >= start:
copy[copyIndex] = data[i]
copyIndex -= 1
i -= 1
while j >= start + length + 1:
copy[copyIndex] = data[j]
copyIndex -= 1
j -= 1
#data[start:end+1] = copy[start:end+1]
print(start, end, data, copy)
return leftCount + rightCount + count
def InversePairs(self, data):
# write code here
if data == []:
return 0
copy = data[:]
#copy = [0] * len(data)
return (self.RecursionCount(data, copy, 0, len(data) - 1) % 1000000007)
但是這種解法會超時,造成時間複雜度過高,有兩個原因:
- copy初始化沒有必要完全拷貝data,可以隨便初始化
- 歸併排序採用分治法,data與copy同步同樣在遞迴的過程中,採用分治法的思想拷貝
通過的程式碼
class Solution:
def RecursionCount(self, data, copy, start, end):
#print(start, end, data, copy)
if start >= end:
copy[start] = data[start]
return 0
count = 0
length = int((end - start) / 2)
leftCount = self.RecursionCount(data, copy, start, start + length)
rightCount = self.RecursionCount(data, copy, start + length + 1, end)
#data = copy[:] #排序好之後,data要拷貝copy,才能保證data兩邊是排好序的。
i, j = start + length, end
copyIndex = end
while i >= start and j >= start + length + 1:
if data[i] > data[j]:
copy[copyIndex] = data[i]
copyIndex -= 1
i -= 1
count += (j - start - length)
else:
copy[copyIndex] = data[j]
copyIndex -= 1
j -= 1
#比較之後,可能有一邊沒遍歷完,copy可能沒被全部填滿,需要繼續填充copy
while i >= start:
copy[copyIndex] = data[i]
copyIndex -= 1
i -= 1
while j >= start + length + 1:
copy[copyIndex] = data[j]
copyIndex -= 1
j -= 1
data[start:end+1] = copy[start:end+1]
#print(start, end, data, copy)
return leftCount + rightCount + count
def InversePairs(self, data):
# write code here
if data == []:
return 0
#copy = data[:]
copy = [0] * len(data)
return (self.RecursionCount(data, copy, 0, len(data) - 1) % 1000000007)
data = [7,5,6,4]
print(Solution().InversePairs(data))
輸出中間結果可以看到,將data陣列使用了歸併排序演算法進行了排序:
0 3 [7, 5, 6, 4] [0, 0, 0, 0]
0 1 [7, 5, 6, 4] [0, 0, 0, 0]
0 0 [7, 5, 6, 4] [0, 0, 0, 0]
1 1 [7, 5, 6, 4] [7, 0, 0, 0]
0 1 [5, 7, 6, 4] [5, 7, 0, 0]
2 3 [5, 7, 6, 4] [5, 7, 0, 0]
2 2 [5, 7, 6, 4] [5, 7, 0, 0]
3 3 [5, 7, 6, 4] [5, 7, 6, 0]
2 3 [5, 7, 4, 6] [5, 7, 4, 6]
0 3 [4, 5, 6, 7] [4, 5, 6, 7]
5
