最近一直在看關於PCA有關的東西，PCA是最常用的線性子空間方法，常常用來進行特徵提取，其本質是一個降維的過程，自從一篇文章《PCANet: A Simple Deep Learning Baseline for Image Classification》的發表，為大家提供新的研究思路。

一、主成分分析PCA

　　在談PCA之前，先來看看協方差矩陣的內容。

　　在統計學的基本概念裡，首先有一個含有n個樣本的集合，則樣本的均值、方差、標準差的計算公式如下：

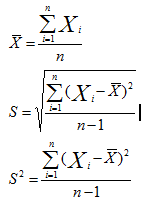
　　至於為什麼是除以n-1，則是出於無偏估計，即能使我們以較小的樣本集更好地逼近總體的標準差。這是一維的情況，如果在二維情況下，方差就變為了協方差，描述的是兩個向量X和Y之間的相關性：

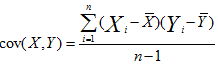
　　但如果是高維情況呢？如X,Y,Z，這時就需要協方差矩陣來描述，它描述的是各維度之間的相關性。

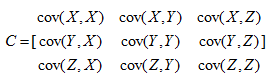
　　主成分分析設法將原來變數重新組合成一組新的互相無關的幾個綜合變數，同時根據實際需要從中可以取出幾個較少的綜合變數儘可能多地反映原來變數的資訊，也是數學上用來降維的一種方法。在數學的角度來看，它實際只是一種對映：

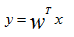
其中x是原始資料，y是對映後的向量，w即對映矩陣，這裡是x的協方差矩陣的特徵向量，通常取前K個特徵值所對應的特徵向量。以一個含有10個樣本的X矩陣為例，其中每個樣本Xi都是50*1的列向量，其演算法的計算步驟如下：

　　（1）特徵中心化：即每一維的樣本都減去它的均值，此時X仍為50*10的矩陣

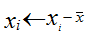　　（2）計算中心化後的協方差矩陣，得到矩陣C為50*50

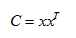
　　（3）計算C的特徵值和特徵矩陣：[V,D]=eig(C)

　　（4）選取前K個特徵值，構造對映矩陣。

這裡有兩點需要注意：

【注】1.在有些文章中對於協方差矩陣的求法有不同表述，C也被表述為X的轉置乘以X，這裡我做如下解釋，假如在樣本矩陣中，每一列代表一個樣本，即50*10，則根據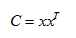

的計算公式，得到C為50*50的協方差矩陣，則C的特徵向量為50*1，再根據

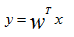
得到符合的y為1*10；但假如在樣本矩陣中，每一行代表一個樣本，即10*50，則應根據

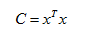
的計算公式，得到C為50*50的協方差矩陣，則C的特徵向量為50*1，再根據

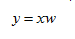
得到符合的y為10*1；即根據樣本的排列順序不同，協方差矩陣的求法不同。

　　 2.在假設K=1的情況下，假設輸入樣本為50*10，輸出卻為1*10，即降維的程度是1/50，其降維的程度與樣本的維度與選取的特徵向量個數有關。

二、Deep PCA

　　在文章《Face Recognition Using Deep PCA》中提出了一種Deep PCA,實際是一種PCA的級聯，即兩層PCA,模型中利用第一層產生的資訊再送入產生一個新的不同的表述，使之更具有識別力；為了去除資料間的相關性，模型在每層PCA前加入ZCA白化，其結構如圖所示：

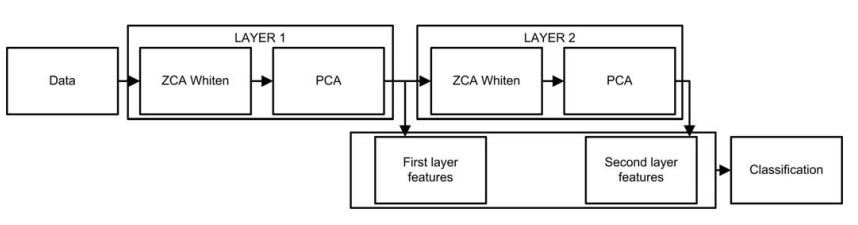
　　從圖中可以看出，原始資料經過第一層PCA，得到第一層的特徵w1，再進入第二層的PCA，得到第二層的特徵w2，最終兩層的特徵融合得到最終的分類結果。其大致演算法如下

　　（1）ZCA白化：ZCA白化的過程實際是去相關性的過程，它實際也是利用特徵中心化後的協方差矩陣的特徵向量來實現的，只是相比PCA白化，它更接近原始資料。

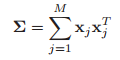
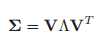
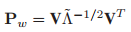
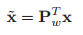
　　（2）特徵提取：特徵提取的過程實際就是實現兩層PCA的過程

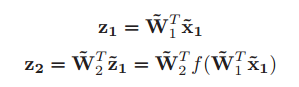
 　　其中Z1和Z2分別是兩層PCA的輸出，f函式代表白化處理後的結果。Z2充分利用了第一層的表達去提取新的特徵，如此，在對整體影象的把握上每一層都有新的不同的表達。

　　（3）特徵融合：Deep PCA將第一層和第二層的特徵融合後作為提取到的特徵，但只是進行了簡單的級聯，

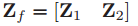
　　在我看來，有這樣一個問題，由於Z2是根據Z1提取出來的，兩者必然存在關聯，或者說這樣直接融合肯定會有資料冗餘的存在，資料冗餘的存在是否會影響效能？實際上不會，因為研究表明，對於多層網路結構而言，每層的特徵均具有不同的意義，淺層資訊更多的是表現的是影象的整體特證，而深層資訊更多的表現的是影象的紋理特徵，或者說是抽象資訊。

三、 PCANet 

　　到這裡才到了這篇部落格的重點：PCANet，來源於文獻《PCANet: A Simple Deep Learning Baseline for Image Classification》?，在這篇文章中提出了一個用於影象分類的簡單深度學習網路：PCANet。在這個框架中，首先通過PCA方法來學習多層濾波器核，然後使用二值化雜湊編碼以及塊直方圖特徵來進行下采樣和編碼操作。相比於Deep PCA，雖然兩個都是 PCA方法的兩層級聯，但效果已然大不同。

　　（1）Deep PCA的每層濾波器核（對映核）只有一個，而PCANet有多個在文章中取L1=L2=8;即每層都是8個濾波核，最終對於每個樣本會有64個表述，這也是導致PCANet的特徵輸出高達幾十萬維的原因之一。

　　（2）Deep PCA在預處理時對影象進行白化處理，在輸出時進行層間融合，這都是PCANet沒有的內容；PCANet直接把第二層的輸出送到輸出模組，即使用二值化雜湊編碼以及塊直方圖特徵來進行下采樣和編碼操作。

　　（3）PCANet在進行資料採集時，雖也是直接對畫素進行操作，但加入了塊取樣的操作，這樣做有兩個好處，一是加入了畫素的鄰域資訊；二是升維，PCA方法不可避免的一個效果就是降維，然而PCANet在效果上並沒有表現降維，反而資料增多了，而有用的資料越大，越利於分類。

　　下面介紹的PCANet網路結構預算實現，其結構如下：

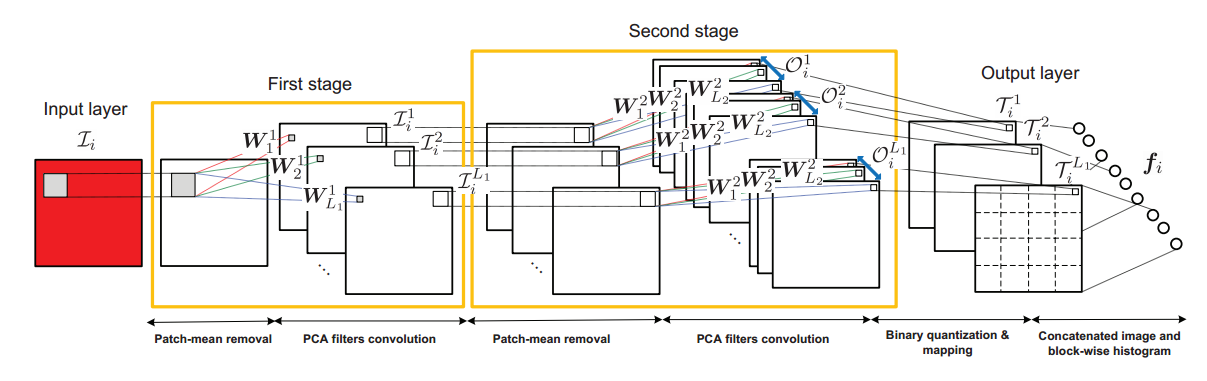
　　這裡程式碼以中設定的PCANet引數來解說這個結構。

　　（1）預處理：預處理的過程就是塊取樣的過程，令輸入的第i張圖片為Ii，然後進行塊取樣，取樣塊大小設定為7*7，對每一個畫素進行塊取樣，進行特徵中心化後，得到第i張圖片的輸入資料：

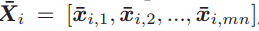
 　 若m=n=64，在程式中顯示為49*4064的矩陣。則總體的樣本矩陣表示為

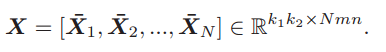
　　（2）特徵提取：特徵提取的過程就是主成分分析的過程。包括求取協方差矩陣（49*49），選取前L1個特徵值和特徵向量。在這裡L1=8是濾波器的數量，對應的PCA濾波器表示如下：

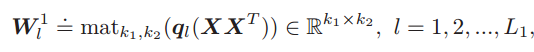
　　這個方程的含義就是提取X的協方差矩陣的前L1個最大特徵值對應的特徵向量來組成特徵對映矩陣。這裡區別於Deep PCA的一點是沒有將所有特徵向量組合起來構成特徵矩陣，而是單個重構成特徵對映矩陣，因此這裡會有8個濾波器，而不是一個。對於每一層的輸出，採用了影象卷積的概念。對於每一幅影象來說，均有8個輸出。

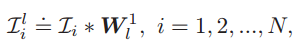
　　在這裡需要注意卷積之前要對樣本進行邊緣補0操作，以保證卷積前後樣本大小相同，都是49*4096。第二層的結構與第一層完全相同，第二層的濾波器數L2=8

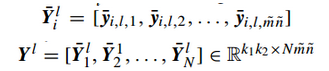
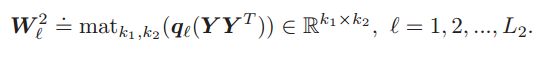
　　第二層的輸出後對應每個影象有64的表述。

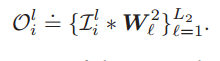
　　（3）輸出層：輸出層首先對輸出矩陣進行二值化處理，使其只包含1和0；在此基礎再進行雜湊編碼 ，使每個畫素值都變為0-255之間的一個數，量化並加大各特徵的差異。

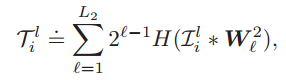
　　之後對於第一層的每個輸出矩陣(8*N)，將其分為B塊，計算統計每個塊的直方圖資訊，然後在將各個塊的直方圖特徵進行級聯，最終得到塊擴充套件直方圖特徵：

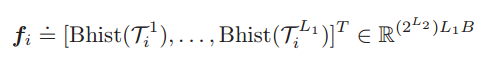
　　以上就是所有PCANet的內容，PCANet中不但沒有降維，反而升維，輸出資料達到幾十萬維，即使用最簡單的k近鄰分類器，也能達到較好的效果，這正是其強大之處。