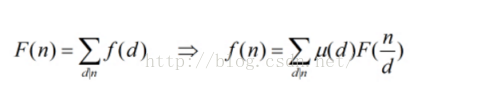原文地址

   前兩天學習了一下之前一直覺得高大上並且想學的內容——莫比烏斯反演。不過學任何東西都是一樣，學會了發現也就這樣，雖然只是皮毛。OK，廢話不多說，進入正題，今天我用杭電的1695這道題再來溫習一下莫比烏斯反演。

   HDU1695的題目大意是這樣的，給你 a , b , c , d , k 五個值 （題目說明了 你可以認為 a=c=1）  x 屬於 [1,b] ，y屬於[1,d]  讓你求有多少對這樣的 （x,y）滿足gcd（x,y）==k。給你的時間是 3000 MS。   0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000

   這道題我剛開始看的時候想到的是容斥定理， 由於以前沒用容斥寫過題，但久聞莫比烏斯反演大名，乾脆就學習了一下，如何用莫比烏斯反演來解題。

   首先 ，這道題可以進行一部分的簡化，因為  gcd（x,y）=k  那麼，很顯然 gcd（x / k,y / k）是等於 1 的（x,y 除了 k 一定沒有其他的公因數）。那麼，此時問題就可以轉化為： x 屬於 [1,b / k] ，y屬於[1,d / k]  讓你求有多少對這樣的 （x,y）滿足gcd（x,y）== 1 即x和y是互質的。 走到這一步 ，題目算是解決了一半了，我們先來看一下什麼是莫比烏斯反演。

   這裡先給出莫比烏斯的兩個公式 ：  （以下圖片摘自 ACdreamer 的部落格，僅供學習交流使用）

OK 這兩個就是莫比烏斯反演的兩種表現形式 反演的核心所在是莫比烏斯函式，什麼是莫比烏斯函式呢？ 我們在下面給出它的定義：

   是的 沒錯 我們稱之為 mu 函式，它就是莫比烏斯函式，也是整個反演的最為重要的部分。

   現在我們來繼續解決上面的那個問題。如何去求有多少對這樣的 （x,y）滿足gcd（x,y）== 1 。這個問題你直接拿到手發現確實比較麻煩，但是換個思路，如果我們去求有多少對這樣的 （x,y）滿足 gcd（x,y）== 1 的倍數  呢？  是不是就非常簡單了呢？   

   OK ！ 我們試著來設一下 F（d）為 有多少對（x,y）滿足 gcd（x,y）== d 的倍數 。

 f（d）為有多少對（x,y）滿足 gcd（x,y）== d  。

   呵呵，你發現F（d）用初中數學都能求出是 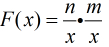  (n=b / k，m=d / k)

   那麼其實我們需要解決的就剩下如何求出 f（1）是多少的問題了。

   根據公式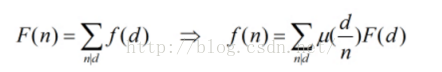你可以發現，在你對函式進行題設時是需要滿足反演對函式的要求的，這個需要你自己來體會，至於另一個公式的設法是 “約數” 的關係，而這個則是 “倍數” 的關係。

  那麼問題就基本上解決了，f（1）= mu（1）*F（1）+ mu（2）*F（2）+……  這個式子的終止條件是什麼呢？很顯然在所限定的區間內，d最大為 min（m,n）。

那麼完整的式子就應該是  f（1）= mu（1）*F（1）+ mu（2）*F（2）+……mu（min（m,n））*F（min（m,n））。至此 這道題目就順利的解決了。

下面給出如何求 mu 函式的程式碼 下列程式碼求得了 mu 函式 1-n 的函式值，直接使用就行

第一種 普通篩選求莫比烏斯函式 時間複雜度為  O（nlogn）

void getMu(){
    int N=maxn;
 for(int i=1;i<N;++i){
        int target=i==1?1:0;
        int delta=target-mu[i];
        mu[i]=delta;
     for(int j=2*i;j<N;j+=i)
          mu[j]+=delta;
    }
}

void Init(){
    int N=maxn;
    memset(prime,0,sizeof(prime));
    memset(mu,0,sizeof(mu));
    memset(vis,0,sizeof(vis));
    mu[1] = 1;
    cnt = 0;
    for(int i=2; i<N; i++){
        if(!vis[i]){
            prime[cnt++] = i;
            mu[i] = -1;
        }
        for(int j=0; j<cnt&&i*prime[j]<N; j++){
            vis[i*prime[j]] = 1;
            if(i%prime[j]) mu[i*prime[j]] = -mu[i];
            else{
                mu[i*prime[j]] = 0;
                break;
            }
        }
    }
}

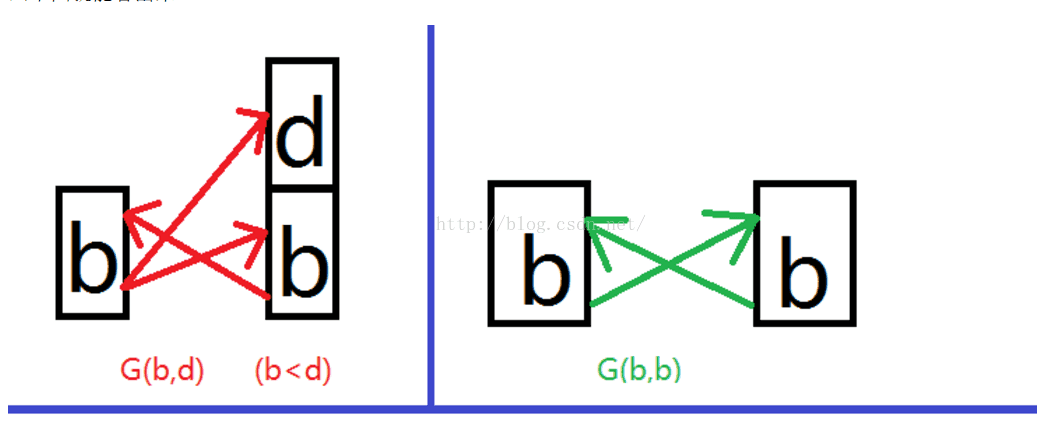
此時，走到這一步，我們已經求得了（x,y）滿足 gcd（x,y）=1 的對數 ，但題目中說明了，（1，2）和（2，1）算一種情況，那麼我們就要減去多餘了的情況，怎那麼找出那些多算進去的情況呢？ 下面的圖畫的很清楚：

   G（b,b）就是多算進去的這些情況，

   那麼 G（b，d）- G（b，b）/ 2 就是最終我們要求的結果了，至於這一點，有不懂的請在紙上畫一畫，這不是我要講的重點了。

   完整程式碼如下：

#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+7;
bool vis[maxn];
int prime[maxn],mu[maxn];
int cnt;
void Init(){
    int N=maxn;
    memset(prime,0,sizeof(prime));
    memset(mu,0,sizeof(mu));
    memset(vis,0,sizeof(vis));
    mu[1] = 1;
    cnt = 0;
    for(int i=2; i<N; i++){
        if(!vis[i]){
            prime[cnt++] = i;
            mu[i] = -1;
        }
        for(int j=0; j<cnt&&i*prime[j]<N; j++){
            vis[i*prime[j]] = 1;
            if(i%prime[j]) mu[i*prime[j]] = -mu[i];
            else{
                mu[i*prime[j]] = 0;
                break;
            }
        }
    }
}
void getMu(){
    int N=maxn;
    for(int i=1;i<N;++i){
       int target=i==1?1:0;
       int delta=target-mu[i];
       mu[i]=delta;
        for(int j=2*i;j<N;j+=i)
         mu[j]+=delta;
   }
}
int main()
{
    ios::sync_with_stdio(false);
    int a,b,c,d,k;
    int T,Case=0;
    Init();
    cin>>T;
    while(T--){
        cin>>a>>b>>c>>d>>k;
        cout<<"Case "<<++Case<<": ";
        if(k==0){
            cout<<"0"<<endl;
            continue;
        }
        b/=k,d/=k;
        long long ans1=0,ans2=0;
        for(int i=1;i<=min(b,d);i++){
            ans1+=(long long)mu[i]*(b/i)*(d/i);
        }
        for(int i=1;i<=min(b,d);i++){
            ans2+=(long long)mu[i]*(min(b,d)/i)*(min(b,d)/i);
        }
        cout<<ans1-ans2/2<<endl;
    }
    return 0;
}

   至此我們通過HDU1695學習了莫比烏斯反演的入門，數論中還有更多有趣的問題等待我們去探索，不得不感嘆這些數學家們的偉大了。

        </div>
            </div>
        </article>