2. 程式人生 > >Matlab中插值函式彙總和使用說明

Matlab中插值函式彙總和使用說明

阿新 • • 發佈：2018-12-09

注：該文從連結地址http://blog.sciencenet.cn/blog-457143-679275.html轉載。

MATLAB中的插值函式為interp1，其呼叫格式為：  yi= interp1(x,y,xi,’method’)           

其中x，y為插值點，yi為在被插值點xi處的插值結果；x,y為向量， ‘method’表示採用的插值方法，MATLAB提供的插值方法有幾種： ‘method’是最鄰近插值， ‘linear’線性插值； ‘spline’三次樣條插值； ‘cubic’立方插值．預設時表示線性插值

    注意：所有的插值方法都要求x是單調的，並且xi不能夠超過x的範圍。

例如：在一 天24小時內，從零點開始每間隔2小時測得的環境溫度資料分別為

            12，9，9，10，18 ，24，28，27，25，20，18，15，13，

推測中午12點（即13點）時的溫度．

x=0:2:24;        y=[12   9   9   10   18  24   28   27   25   20  18  15  13];

a=13;       y1=interp1(x,y,a,’spline’)

結果為：  27.8725

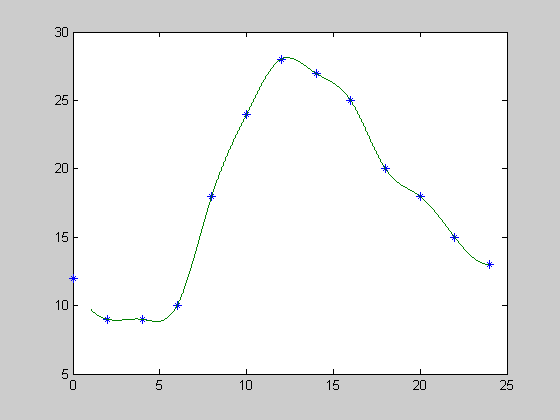
若要得到一天24小時的溫度曲線，則：

xi=0:1/3600:24;

yi=interp1(x,y,xi, ‘spline’);

plot(x,y,’o’ ,xi,yi)

命令1 interp1功能 一維資料插值（表格查詢）。該命令對資料點之間計算內插值。它找出一元函式f(x)在中間點的數值。其中函式f(x)由所給資料決定。x：原始資料點Y：原始資料點xi：插值點Yi：插值點格式(1)yi = interp1(x,Y,xi) 返回插值向量yi，每一元素對應於參量xi，同時由向量x 與Y 的內插值決定。參量x 指定資料Y 的點。若Y 為一矩陣，則按Y 的每列計算。yi 是階數為length(xi)*size(Y,2)的輸出矩陣。(2)yi = interp1(Y,xi) 假定x=1:N，其中N 為向量Y 的長度，或者為矩陣Y 的行數。
(3)yi = interp1(x,Y,xi,method) 用指定的演算法計算插值：’nearest’：最近鄰點插值，直接完成計算；’linear’：線性插值（預設方式），直接完成計算；’spline’：三次樣條函式插值。對於該方法，命令interp1 呼叫函式spline、ppval、mkpp、umkpp。這些命令生成一系列用於分段多項式操作的函式。命令spline 用它們執行三次樣條函式插值；’pchip’：分段三次Hermite 插值。對於該方法，命令interp1 呼叫函式pchip，用於對向量x 與y 執行分段三次內插值。該方法保留單調性與資料的外形；’cubic’：與’pchip’操作相同；’v5cubic’：在MATLAB 5.0 中的三次插值。對於超出x 範圍的xi 的分量，使用方法’nearest’、’linear’、’v5cubic’的插值演算法，相應地將返回NaN。對其他的方法，interp1 將對超出的分量執行外插值演算法。(4)yi = interp1(x,Y,xi,method,’extrap’) 對於超出x 範圍的xi 中的分量將執行特殊的外插值法extrap。(5)yi = interp1(x,Y,xi,method,extrapval) 確定超出x 範圍的xi 中的分量的外插值extrapval，其值通常取NaN 或0。例1 

  1. >>x = 0:10; y = x.*sin(x);

  2. >>xx = 0:.25:10; yy = interp1(x,y,xx);

  3. >>plot(x,y,’kd’,xx,yy)

複製程式碼 例2 

  1. >> year = 1900:10:2010;

  2. >> product = [75.995 91.972 105.711 123.203 131.669 150.697 179.323 203.212 226.505

  3. 249.633 256.344 267.893 ];

  4. >>p1995 = interp1(year,product,1995)

  5. >>x = 1900:1:2010;

  6. >>y = interp1(year,product,x,’pchip’);

  7. >>plot(year,product,’o’,x,y)

複製程式碼 插值結果為： 

  1. p1995 =

  2. 252.9885

複製程式碼 命令2 interp2功能 二維資料內插值（表格查詢）格式 (1)ZI = interp2(X,Y,Z,XI,YI) 返回矩陣ZI，其元素包含對應於參量XI 與YI（可以是向量、或同型矩陣） 的元素， 即Zi(i,j) ←[Xi(i,j),yi(i,j)]。使用者可以輸入行向量和列向量Xi 與Yi，此時，輸出向量Zi 與矩陣meshgrid(xi,yi)是同型的。同時取決於由輸入矩陣X、Y 與Z 確定的二維函式Z=f(X,Y)。參量X 與Y 必須是單調的，且相同的劃分格式，就像由命令meshgrid 生成的一樣。若Xi與Yi 中有在X 與Y範圍之外的點，則相應地返回nan（Not a Number）。(2)ZI = interp2(Z,XI,YI) 預設地，X=1:n、Y=1:m，其中[m,n]=size(Z)。再按第一種情形進行計算。(3)ZI = interp2(Z,n) 作n 次遞迴計算，在Z 的每兩個元素之間插入它們的二維插值，這樣，Z 的階數將不斷增加。interp2(Z)等價於interp2(z,1)。(4)ZI = interp2(X,Y,Z,XI,YI,method) 用指定的演算法method 計算二維插值：’linear’：雙線性插值演算法（預設演算法）；’nearest’：最臨近插值；’spline’：三次樣條插值；’cubic’：雙三次插值。例3： 

  1. >>[X,Y] = meshgrid(-3:.25:3);

  2. >>Z = peaks(X,Y);

  3. >>[XI,YI] = meshgrid(-3:.125:3);

  4. >>ZZ = interp2(X,Y,Z,XI,YI);

  5. >>surfl(X,Y,Z);hold on;

  6. >>surfl(XI,YI,ZZ+15)

  7. >>axis([-3 3 -3 3 -5 20]);shading flat

  8. >>hold off

複製程式碼 例4： 

  1. >>years = 1950:10:1990;

  2. >>service = 10:10:30;

  3. >>wage = [150.697 199.592 187.625

  4. 179.323 195.072 250.287

  5. 203.212 179.092 322.767

  6. 226.505 153.706 426.730

  7. 249.633 120.281 598.243];

  8. >>w = interp2(service,years,wage,15,1975)

複製程式碼 插值結果為： 

  1. w =

  2. 190.6288

複製程式碼 命令3 interp3功能 三維資料插值（查表）格式 (1)VI = interp3(X,Y,Z,V,XI,YI,ZI) 找出由參量X,Y,Z決定的三元函式V=V(X,Y,Z)在點（XI,YI,ZI）的值。參量XI,YI,ZI 是同型陣列或向量。若向量參量XI,YI,ZI 是不同長度，不同方向（行或列）的向量，這時輸出參量VI 與Y1,Y2,Y3 為同型矩陣。其中Y1,Y2,Y3 為用命令meshgrid(XI,YI,ZI)生成的同型陣列。若插值點(XI,YI,ZI)中有位於點(X,Y,Z)之外的點，則相應地返回特殊變數值NaN。(2)VI = interp3(V,XI,YI,ZI) 預設地， X=1:N ，Y=1:M， Z=1：P ，其中，[M,N,P]=size(V)，再按上面的情形計算。(3)VI = interp3(V,n) 作n 次遞迴計算，在V 的每兩個元素之間插入它們的三維插值。這樣，V 的階數將不斷增加。interp3(V)等價於interp3(V,1)。(4)VI = interp3(……,method) %用指定的演算法method 作插值計算：‘linear’：線性插值（預設演算法）；‘cubic’：三次插值；‘spline’：三次樣條插值；‘nearest’：最鄰近插值。說明 在所有的演算法中，都要求X,Y,Z 是單調且有相同的格點形式。當X,Y,Z 是等距且單調時，用演算法’*linear’，’*cubic’，’*nearest’，可得到快速插值。例5 

  1. >>[x,y,z,v] = flow(20);

  2. >>[xx,yy,zz] = meshgrid(.1:.25:10, -3:.25:3, -3:.25:3);

  3. >>vv = interp3(x,y,z,v,xx,yy,zz);

  4. >>slice(xx,yy,zz,vv,[6 9.5],[1 2],[-2 .2]); shading interp;colormap cool

複製程式碼 命令4 interpft功能 用快速Fourier 演算法作一維插值格式 (1)y = interpft(x,n) 返回包含周期函式x 在重取樣的n 個等距的點的插值y。若length(x)=m，且x 有采樣間隔dx，則新的y 的取樣間隔dy=dx*m/n。注意的是必須n≥m。若x 為一矩陣，則按x 的列進行計算。返回的矩陣y 有與x 相同的列數，但有n 行。(2)y = interpft(x,n,dim) 沿著指定的方向dim 進行計算命令5 griddata功能 資料格點格式 (1)ZI = griddata(x,y,z,XI,YI) 用二元函式z=f(x,y)的曲面擬合有不規則的資料向量x,y,z。griddata 將返回曲面z 在點（XI,YI）處的插值。曲面總是經過這些資料點（x,y,z）的。輸入參量（XI,YI）通常是規則的格點（像用命令meshgrid 生成的一樣）。XI 可以是一行向量，這時XI 指定一有常數列向量的矩陣。類似地，YI 可以是一列向量，它指定一有常數行向量的矩陣。(2)[XI,YI,ZI] = griddata(x,y,z,xi,yi) 返回的矩陣ZI 含義同上，同時，返回的矩陣XI,YI 是由行向量xi 與列向量yi 用命令meshgrid 生成的。(3)[XI,YI,ZI] = griddata(…….,method) 用指定的演算法method 計算：‘linear’：基於三角形的線性插值（預設演算法）；‘cubic’： 基於三角形的三次插值；‘nearest’：最鄰近插值法；‘v4’：MATLAB 4 中的griddata 演算法。命令6 spline功能 三次樣條資料插值格式 (1)yy = spline(x,y,xx) 對於給定的離散的測量資料x,y（稱為斷點），要尋找一個三項多項式y = p(x) ，以逼近每對資料(x,y)點間的曲線。過兩點(xi, yi) 和(xi+1, yi+1) 只能確定一條直線，而通過一點的三次多項式曲線有無窮多條。為使通過中間斷點的三次多項式曲線具有唯一性，要增加兩個條件（因為三次多項式有4 個係數）：a．三次多項式在點(xi, yi) 處有： p¢i(xi) = p¢i(xi) ；b．三次多項式在點(xi+1, yi+1) 處有： p¢i(xi+1) = pi¢(xi+1) ；c．p(x)在點(xi, yi) 處的斜率是連續的（為了使三次多項式具有良好的解析性，加上的條件）；d．p(x)在點(xi, yi) 處的曲率是連續的；對於第一個和最後一個多項式，人為地規定如下條件：①． p¢1¢(x) = p¢2¢(x)②． p¢n¢(x) = p¢n¢-1(x)上述兩個條件稱為非結點(not-a-knot)條件。綜合上述內容，可知對資料擬合的三次樣條函式p(x)是一個分段的三次多項式：ï ïîï ïí죠££ ££ £=n n n+12 2 31 1 2p (x) x x xp (x) x x xp (x) x x xp(x)L L L L其中每段pi(x) 都是三次多項式。該命令用三次樣條插值計算出由向量x 與y 確定的一元函式y=f(x)在點xx 處的值。若參量y 是一矩陣，則以y 的每一列和x 配對，再分別計算由它們確定的函式在點xx 處的值。則yy 是一階數為length(xx)*size(y,2)的矩陣。(2)pp = spline(x,y) 返回由向量x 與y 確定的分段樣條多項式的係數矩陣pp，它可用於命令ppval、unmkpp 的計算。例6對離散地分佈在y=exp(x)sin(x)函式曲線上的資料點進行樣條插值計算： 

  1. >>x = [0 2 4 5 8 12 12.8 17.2 19.9 20]; y = exp(x).*sin(x);

  2. >>xx = 0:.25:20;

  3. >>yy = spline(x,y,xx);

  4. >>plot(x,y,’o’,xx,yy)

複製程式碼 命令7 interpn功能 n 維資料插值（查表）格式 (1)VI = interpn(X1,X2,,,Xn,V,Y1,Y2,⋯,Yn) %返回由參量X1,X2,…,Xn,V 確定的n 元函式V=V(X1,X2,…,Xn)在點（Y1,Y2,…,Yn）處的插值。參量Y1,Y2,…,Yn 是同型的矩陣或向量。若Y1,Y2,…,Yn 是向量，則可以是不同長度，不同方向（行或列）的向量。它們將通過命令ndgrid生成同型的矩陣， 再作計算。若點(Y1,Y2,…,Yn) 中有位於點（X1,X2,…,Xn）之外的點，則相應地返回特殊變數NaN。VI = interpn(V,Y1,Y2,⋯,Yn) %預設地，X1=1:size(V,1)，X2=1:size(V,2)，… ，Xn=1:size(V,n)，再按上面的情形計算。VI = interpn(V,ntimes) %作ntimes 次遞迴計算，在V 的每兩個元素之間插入它們的n 維插值。這樣，V 的階數將不斷增加。interpn(V)等價於interpn(V, 1)。VI = interpn(⋯,method) %用指定的演算法method 計算：‘linear’：線性插值（預設演算法）；‘cubic’：三次插值；‘spline’：三次樣條插值法；‘nearest’：最鄰近插值演算法。命令8 meshgrid功能 生成用於畫三維圖形的矩陣資料。格式 [X,Y] = meshgrid(x,y) 將由向量x，y（可以是不同方向的）指定的區域[min(x)，max(x) ， min(y) ， max(y)] 用直線x=x(i),y=y(j) （ i=1,2,…,length(x) ，j=1,2,…,length(y)）進行劃分。這樣，得到了length(x)*length(y)個點，這些點的橫座標用矩陣X 表示，X 的每個行向量與向量x 相同；這些點的縱座標用矩陣Y 表示，Y 的每個列向量與向量y 相同。其中X,Y可用於計算二元函式z=f(x,y)與三維圖形中xy 平面矩形定義域的劃分或曲面作圖。[X,Y] = meshgrid(x) %等價於[X,Y]=meshgrid(x,x)。[X,Y,Z] = meshgrid(x,y,z) %生成三維陣列X,Y,Z，用於計算三元函式v=f(x,y,z)或三維容積圖。例7 

  1. [X,Y] = meshgrid(1:3,10:14)

複製程式碼 計算結果為： 

  1. X =

  2. 1 2 3

  3. 1 2 3

  4. 1 2 3

  5. 1 2 3

  6. 1 2 3

  7. Y =

  8. 10 10 10

  9. 11 11 11

  10. 12 12 12

  11. 13 13 13

  12. 14 14 14

複製程式碼 命令9 ndgrid功能 生成用於多維函式計算或多維插值用的陣列格式 [X1,X2,…,Xn] = ndgrid(x1,x2,…,xn) %把通過向量x1,x2,x3…,xn 指定的區域轉換為陣列x1,x2,x3,…,xn 。這樣， 得到了 length(x1)*length(x2)*…*length(xn)個點，這些點的第一維座標用矩陣X1 表示，X1 的每個第一維向量與向量x1 相同；這些點的第二維座標用矩陣X2 表示，X2 的每個第二維向量與向量x2 相同；如此等等。其中X1,X2,…,Xn 可用於計算多元函式y=f(x1,x2,…,xn)以及多維插值命令用到的陣列。[X1,X2,…,Xn] = ndgrid(x) %等價於[X1,X2,…,Xn] = ndgrid(x,x,…,x)命令10 table1功能 一維查表格式 Y = table1(TAB,X0) %返回用表格矩陣TAB 中的行線性插值元素，對X0（TAB的第一列查詢X0）進行線性插值得到的結果Y。矩陣TAB 是第一列包含關鍵值，而其他列包含資料的矩陣。X0 中的每一元素將相應地返回一線性插值行向量。矩陣TAB 的第一列必須是單調的。例8 

  1. >>tab = [(1:4)’ hilb(4)]

  2. >>y = table1(tab,[1 2.3 3.6 4])

複製程式碼 查表結果為： 

  1. >>tab = [(1:4)’ hilb(4)]

  2. >>y = table1(tab,[1 2.3 3.6 4])

相關推薦

Matlab中插值函式彙總和使用說明

注：該文從連結地址http://blog.sciencenet.cn/blog-457143-679275.html轉載。 MATLAB中的插值函式為interp1，其呼叫格式為：  yi= interp1(x,y,xi,’method’)            其中x，y為插值點，yi為在被插值點

matlab中的interp2插值函式

看了好多文章才大體明白插值的含義，(⊙﹏⊙)b，這理解能力也是醉了.....為了記住這個慘痛教訓，在吃飯前要把看到的文章總結一下~~ interp2 功能 二維資料內插值 格式 (1)ZI = interp2(X,Y,Z,XI,YI) 好多文章裡巴拉巴拉說了一堆，迷迷

matlab中二維插值函式interp2的使用

下面是一段產生log-normal分佈的程式碼，以此進行說明。  clear all; clc; for t=1:100 Traffic(t) =curve(t); end MaxTraffic = max(Traffic); w = 0.2; Wmax = 2*pi*w/3000; x=[0:10

曲線座標系與直角座標系轉換（一）——基礎：matlab插值函式簡介

一、概念與應用 1、概念 插值法又稱“內插法”，是利用函式f (x)在某區間中已知的若干點的函式值，作出適當的特定函式，在區間的其他點上用這特定函式的值作為函式f (x)的近似值，這種方法稱為插值法。如果這特定函式是多項式，就稱它為插值多項式(百度百科) 插值法作用——有效預測未知點

Matlab實現拉格朗日插值函式

function yy=lagrange(x1,y1,xx) %本程式為Lagrange1插值，其中x1,y1 %為插值節點和節點上的函式值，輸出為插值點xx的函式值， %xx可以是向量。 syms x

[數學建模(六)]使用MATLAB實現插值

數值 font 多項式 not new pie 插值法 包含 data 常用的插值：拉格朗日多項式插值、牛頓插值、分段線性插值、Hermite 插值和三次樣條插值。 1.拉格朗日插值法 function y=lagrange(x0,y0,x); n=length(x0)

Matlab 中的copyfile函式使用小記

       因為最近使用labelImg軟體標註訓練圖片，我把標記好的圖片和標註檔案放置在一個資料夾下，由於有多批次圖片標註，每標註一批放在一個資料夾下，最終放置的資料夾如下： 現在我需要把這些資料夾下的圖片和標註檔案集中到兩個檔案ImSet(

Matlab 中的movefile函式使用小記

       因為最近使用labelImg軟體標註訓練圖片，如果圖片有目標區域就標註，沒有當然就不用就標註了，標註檔案儲存在當前圖片資料夾下，這樣當標註完一批圖片後你將看到，好多圖片和圖片對應的標註檔案（.xml格式），還有沒有標註的圖片： &n

matlab中的mvnrnd函式用法

使用matlab來實現: clear all;close all; clc; % 第一組資料 mul=[0,0]; % 均值 S1=[.1 0;0 .1]; % 協方差 data1=mvnrnd(mul, S1, 100); % 產生高斯分佈資料 % 第二組資料 mu2=[1.25 1.25

Python字典中取值函式

在Python中當字典的值是函式時，如果這樣寫fou = {'a':aa(),'b'=bb(),'c':cc()}fou['a']這時函式會全部被執行，其實關鍵在後面的括號，經過多次嘗試把字典裡括號去掉函式是沒有立刻執行的也就是沒有返回函式結果，可去掉字典裡函式的括號打印出fou['a']得到的結果是一個物件

15，matlab中的mean函式，求平均

（1） help mean mean   Average or mean value.     S = mean(X) is the mean value of the elements in X if X is a vector.  &nbs

Matlab中的stretchlim函式詳解

imadjust函式是MATLAB的一個工具箱函式，一般的語法呼叫格式為： f1=imadjust（f，[low_in  high_in],[low_out  high_out],gamma） （注：本文所述影象資料均為Uint8，對於Matlab，矩陣中的一個元素即是一

Matlab中使用plot函式動態畫圖方法總結

原文 Matlab除了強大的矩陣運算，模擬分析外，繪圖功能也是相當的強大，靜態畫圖沒什麼問題，由於Matlab本身的多執行緒程式設計缺陷，想要動態的畫圖，並且能夠很好的在GUI中得到控制，還不是一件很容易的事情，下面總結幾種方法。一. AXIS 移動座標系     這種方法

MATLAB--條件插值、二維插值、擬合

%% 樣條邊界條件插值 x=linspace(0,2*pi,15); y=sin(x); plot(x,y,'o') hold on% complete p=csape(x,y,'complete',[2,2]); x1=linspace(0,2*pi,150); y1=pp

matlab中的imshow函式使用

轉自 http://hi.baidu.com/redaiyu1989/item/3f39fe151b446fc039cb3087 網上搜的好東西 一些影象處理函式用法 % imshow imshow是用來顯示圖片的，如 >> I = imread('moon.

MATLAB——數值插值之拉格朗日（Lagrange）插值法

 由於MATLAB中沒有現成的拉格朗日插值命令，因此我們可以根據Lagrange插值法的定義編寫一個Lagrange插值命令。    定義： 給定n個插值節點x1,x2,...,xn和對應的函式值y1,y2,...yn,利用拉格朗日插值多項式公式(注：k從0到n累加)，其

Matlab中布林值/邏輯值與數值型型別的相互轉換

在涉及到一些下標運算時，經常會遇到布林值與數值型的相互轉換。 數值型轉化為邏輯值 在MATLAB中常採用函式logical()將數值型資料轉換成邏輯型資料。數值型資料轉換成邏輯型的資料一般遵循這樣的規則：非0的數值型資料轉換成邏輯真，即1；等於0的數值轉換成邏輯假，即0。那麼按照

MATLAB中K-means函式表達方式

K-means演算法以偶是距離作為相似度測度，它是求對應某一初始聚類中心向量V最優分類，使得評價指標J最小。演算法採用誤差平方和準則函式作為聚類準則函式 K-means聚類演算法採用的是將NP的矩陣X劃分為K個類，使得類內物件之間的距離最大,而類之間的距離最小。

matlab中uint16(uint8)函式的用法

matlab中uint16函式的用法； 1.函式用法：將輸入引數對映到無符號16位範圍之內，即將引數限定在0-65535之間； 2.例項：當輸入為一個實數a時： if a<0 輸出ans=0; if 0<=a<=65535 輸出ans=a; i

Matlab中的eig函式和eigs函式的異同點

                Matlab中的eig（）函式和eigs（）函式的異同點1、相同點      都可以求解矩陣的特徵值和特徵向量2、不同點      eig函式主要是給出矩陣的特徵值和特徵向量      eigs函式主要是通過迭代法來求解矩陣特徵值和特徵向量3、例項>> A = [1