在此之前，針對APS寫了一些理論性的文章；而對於Optaplanner也寫了一些介紹性質，幾少量入門級的幫助初學者走近Optaplanner。在此以後，老農將會按照Optaplanner官方的使用者手冊的結構，按章節地對其進行翻譯，併成型一系列的操作說明文章。在文章中，為了降低對原文的理解難度，有些地方我不會直接按原文件的字面翻譯，而是有可能加入一些我自己的理解，或添一些解釋性的內容。畢竟英語環境下的思維和語言表達方式，跟中文或多或少會有差別的，所以如果全部按字面翻譯，內容就非常生硬，可讀性差，解程難度較大。我認為應該在理解了作者原意的基礎上，再進一步以中文方式的表達，才算是真的的本地化。記得老農還是少農時，學習開發技術，需要閱讀一些外國書箱的翻譯本時，印象最深的是候捷老師的書，儘管《深入淺出MFC》，磚頭厚度的書，硬是被我翻散了線，MFC儘管真的晦澀難懂，但候老卻能把Windows的訊息機制及MFC中整個個巨集體系，系統地通俗地描述出來，令讀者不需要花費太多精力去理解猜測書中字面的意義，大大降低的VC++中MFC的學習門檻。但老農畢竟只是一個一線開發人員，不是專業的技術資料翻譯人才，不可能有候老師的專業水平，因此，我也只可盡我所能把內容儘量描述得通俗一些，讓讀者儘量容易理解，花費更少的時間掌握這些知道要點。

本文以Optaplanner 7.10.0 Final版本的開發手冊作為基礎進行翻譯。

1. Optapplanner 介紹

1.1. 什麼是Optaplanner?

 　　每個組織都需要面對規劃、排程問題：在有限的資源約束下提供服務與產品（例如人員，資產，時間及資本等限制）。Optaplanner可以優化這類規劃、排程問題，令到使用它的組織可以用更少的資源做更多的事（儘可能的花少錢辦大事）。這就是著名的的約束滿足規劃，它屬於運籌學的一部分。

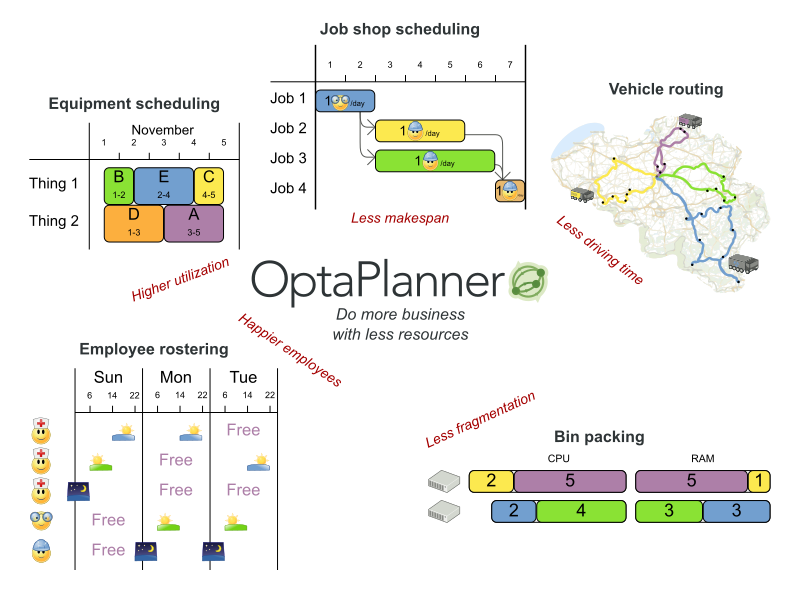
Optaplanner是一個輕量的、可嵌入的，可以對規劃問題進行優化的約束滿足引擎，它可以解決案例有：

• 員工排班：為護士、維修工等人員制定上班時間表。
• 方程安排
  ：安排會議、約見、維修工作、廣告時間等。
• 教育領域的時間安排：安排課程、課堂、考試、會議講座等。
• 規劃車輛運動路線：通過已知的地圖工具，為貨運、客運（貨車、火車、輪船、航班等）規劃交通工具多目標的執行路線。
• 裝箱問題：向容器、貨車、輪船和倉庫裝載貨物，同時可以規劃電腦的資源載入利用，例如雲計算的資源分配問題。
• 車間生產安排：規劃汽車組裝生產線，機器隊規劃，勞動任務的規則等。
• 下料問題：在下料分割的時候，實量最小的浪費，例如切割紙張、鋼鐵、地毯等。
• 運動賽事安排：規劃比賽和訓練，例如安排足球聯賽、棒球聯賽等。
• 金融優化：投資組合優化、實現風險分散等。

1.2. 什麼是規劃問題？

　一個規劃問題，基於有限的資源和指定的約束，有一個優化目標。優化目標可以是多種事物，例如：

• 利潤最大化 - 優化目標得出的結果是儘可以高的利潤。
• 最小化生態足跡（即儘可能減少對生態的影響） - 優化目標是對環境產生儘可能小的影響。
• 最大化員工或客戶的滿足度 - 優化目標重視員工與客戶的需要。

實現這些目標的能力依賴於可用資料的數量，例如：

• 人員數量
• 時間
• 預算
• 特殊資產，例如機臺，車輛，計算機，建築物等。

與這此資源相關的約束也必然計算在內，例如，一個人的工作小時數， 他們可使用（操作）的機臺數量，裝置之間的相容性等。

Optaplanner可以幫助Java程式設計師有效地解決約束滿足問題， 在Optaplanner引擎中，對每個有效的約束分數計算中，組合了啟發式和元啟發式演算法。 

 1.2.1 規劃問題屬於NP-Complete問題或NP-hard問題

　　上述所有的案例或許都屬於NP-complete/NP-hard問題，（什麼是NP-Complete/NP-hard問題呢？），在外行人看來，它的定義是：

　　對於一個問題：

• 在合理時間內可以容易地驗證一個給定的解。
• 在合理時間內，目前尚沒有行之有效的解法，能找到其絕對最優解(注1)。

　　(注1)：至少，到目前為止，仍未有一個世界上最聰明的電腦科學家能找到此方法。可是一旦他們找到對其中一個NP-Complete問題的有效解法，那麼這個方法對所有NP-Complete問題都是可行辦法。事實上，如果任何人只需證明是這種解法的存在與否，即可獲得100萬美元的獎勵。

　　其實這其含義是相當悲觀的：要解決這些問題或許比你預想中更困難，因為目前針對這種問題的常見兩種技術是未足夠解決此類問題的。這兩種方法是：

• 暴力演算法(儘管是一些優化過，相對聰明的暴力演算法變種), 但獲得其解所需的時間非常長(譯者：主要原因是時間複雜度非常高)。
• 快速演算法，例如在Bin packing問題中，先裝入最大項；但得到的解離絕對最優解仍存在相當大距離的。

通過使用一些更高階的演算法，Optaplanner可以在合理的時間內，對這些規劃問題找到相對較優解。

 1.2.2 規劃問題存在約束（包括硬約束與軟體約束)

　　通常來說，一個規劃問題至少包括兩個層次的約束：

• (負面)硬約束，不可被違反。例如：一個教師在同節的時間內不能同時上兩門課。
• (負面)軟體約束，若可避免，它不應該被違反。例如：教師都不太喜歡在週五下午上課。

　　也有些問題存在一些正面的約束：

• 正面分數在可能情況下應該實現。例如：教師B喜歡在週一上午上果。

　　一些比較基礎的規劃問題(例如8王后問題)，只存在硬約束；有一些規劃問題則存在超3層，甚至更多層次的約束。例如：硬約束，中間約束和軟約束。

　　這些約束會被定義在規劃問題的Score calculation裡(也稱為適應度函式)裡。規劃問題裡的每一個解的優劣，都可以通過分數來評價。在Optaplanner中，分數約束是通過面向物件語文編寫的，例如Java程式碼或通過Drools指令碼實現的rules. 這些程式碼相當容易編寫，靈活且易於擴充套件。

 1.2.3 規劃問題存在巨大的搜尋空間

　　一個規劃問題存在非常多的解，這些解可以分為以下數種：

• 可能解：規劃問題的任意一個解都稱作可能解，無論這個解是否違反了約束，或違反了多少約束。規劃問題往往存在令人難以至今的巨量可能解，這裡面很多解是毫無價值的。
• 可行解：規劃問題的可行解是指沒有違反任何（負面）硬約束的解。一個規劃問題的可行解的數量，與其可能解相關。有時也不存在可行解，一個規劃問題的每一個可行解，都是該問題的一個可能解。
• 絕對最優解:絕對最優解是這個規則問題獲得約束分最高的那個解。規劃問題通常只有1個或少量數個絕對最優解。通常存在至少1個絕對最優解，儘管當這個規劃問題不存在可行解，它也存在絕對最優解，這時候絕對最優解就是非可行解。
• 相對最優解:相對最優解是指規劃問題在一定的求解時間內得到評分最高的解。相對最優解通常是可行解，只要有足夠的執行時間，找到的相對最優解就是絕對最優。

　　此外，儘管基於一個較小的資料集描述的一個規劃問題，其可能解的數量通常是非常巨大的（如果計算正確的話）。正如你從示例中可以看到，大多數情況下，一個規劃問題的可能解數量，對目前已知宇宙的原子數量還要多(10的80次方)。因為目前還沒有直接的辦法找出規劃問題的絕對最優解，一些求解實現方法是通過暴力窮舉的方法，至少可以窮舉所有可能解中的一個子集。

　　OptaPlanner支援多種優化演算法，以有效地涉足大量可能解，根據不同使用場景的情況，一些優化演算法的效能比其它演算法更佳，但哪個更佳是無法預先告知的（譯者：需要通過Benchmark等功能測定）。在Optaplanner裡，很容易能過修改幾行XML內容或Java code，來更改求解器的配置，從而切換不同的優化演算法。

【未完，待續...】

原創不易，如果覺得文章對你有幫助，歡迎點贊、評論。文章有疏漏之處，歡迎批評指正。

歡迎轉載，轉載請註明原文連結：http://www.cnblogs.com/kentzhang/p/8709679.html

如果大家有何建議，歡迎大家加我企鵝一起探討：12977379或V信：13631823503。

其實 Optaplanner規劃引擎不需要對Java過份精通即可使用,因為它使用到的都是Java最基本的知道，但還是需要有基本的Java知識才行，希望大家找我研究討論時，如果Java, Maven等方面仍接觸較少，請大家先行自補該方面的知識，本猿暫時只能跟大家探討Optaplanner, Drools的應用，而Java相關的知識，恕無法提供有效的幫助，畢竟本猿也只是個Java新手。先謝了。