資料結構————查詢與排序
複習了幾遍資料結構,線性表、棧、佇列、串、陣列、廣義表、樹、圖、查詢和排序。發現查詢和排序演算法很容易忘,而且這些演算法又是很經典的,其他的掌握結構體和指標稍微好一點,想在此寫下查詢和排序演算法,讓自己更深刻,很多都不好寫,所以有些就沒寫。
查詢
1.基於線性表查詢法 靜態查詢表 不對錶做插入和刪除
順序查詢法 : 就是遍歷一遍進行if判斷 平均查詢長度 (n+1)/2;
int SeqSearch(RecordList l,KeyType k) { l.r[0].key=k;i=l.length; while(l.r[i].key!=k) i--; return i; }
折半查詢法 : 順序儲存,有序排序,優點:比較次數少,查詢速度快,平均效能好;缺點:待查表為有序表,且插入刪除困難,適合用於不經常變動而查詢頻繁的有序列表。 平均查詢長度 log2(n+1)-1
int BinSrch(RecordList l,KeyType k) { low=1;high=l.length; while(low<=high) { mid=(low+high)/2; if(k==l.r[mid].key) return mid; else if(k<l.r[mid].key) high=mid-1; else low=mid+1; }}
分塊查詢法 :效能介於順序查詢和折半查詢之間
25 ->{18,14,12,25 } 58->{8,28,32,45,36,58} 88->{60,88,71}
| 25 | 58 | 88 |
| 18 | 14 | 12 | 25 | 8 | 28 | 32 | 45 | 36 | 58 | 60 | 88 | 71 |
2.基於樹的查詢法 動態查詢表:需要對錶做插入和刪除
二叉排序樹 :
BSTree SearchBST(BSTree bst,KeyType key)
{
if(!bst) return NULL;
else if(bst->key==key) return bst;
else if(bst->key>key) return SearchBST(bst->lchild,key);
else
return SearchBST(bst->rchild,key);
}平衡二叉樹 : 又稱AVL樹,左子樹與右子數的高度之差的絕對值小於等於1,引入平衡二叉排序樹目的:為了提高查詢效率,平均查詢長度為 log2(n)
B樹: 與二叉樹類似,可以定義一種“m叉排序樹”,通常稱為m路查詢樹
如果m路查詢樹為平衡樹時,其查詢效能更好 B樹即為一顆平衡的m路查詢樹,或者空樹
1.樹中每個結點最多有m棵子樹 2.根結點至少有兩棵子樹
3.除根結點之外的所有非葉結點至少有m/2棵子樹
例:具有n個葉結點的m階B樹,至少含有多少個關鍵字? 答:1+(【m/2】-1)*(n-1)
3.計算式查詢法—雜湊法
雜湊法又稱雜湊法、雜湊法或關鍵字地址計演算法
構造雜湊函式 1.數字分析法 2.平方取中法 3.分段疊加法 4.除留餘數法 5.偽隨機數法
處理衝突的方法: 1.開放定址法 2.再雜湊法 3.鏈地址法 4.建立公共溢位區
1.開放定址法 (1)線性探測再雜湊 d=1,2,3,4,5,6················
(2)二次探測再雜湊 d=1*1 ,-1*1,2*2,-2*2,·············k*k,-k*k
(3) 偽隨機數序列 建立一個隨機數發生器
3.鏈地址法 經常進行插入和刪除
排序
1.插入類排序
直接插入排序: 時間複雜度 T=O(n^2); 空間複雜度 S=O(1) 穩定
void InsSort(RecordType r[],int length)
{
for(i=2;i<=length;i++)
{
r[0]=r[i];j=i-1;
while(r[0].key<r[j].key)
{r[j+1]=r[j];i=j-1;}
r[j+1]=r[0];
}}{48} 62 35 77 55 14 35 98
{48 62} 35 77 55 14 35 98
{35 48 62} 77 55 14 35 98
{35 48 62 77} 55 14 35 98
{35 48 55 62 77} 14 35 98
{14 35 48 55 62 77} 35 98
{14 35 35 48 55 62 77} 98
{14 35 35 48 55 62 77 98}
折半插入排序: 時間複雜度O(n^2) 比較時間複雜度 nlogn 空間複雜度 O(1) 不穩定
void BinSort(RecordType r[],int length)
{
for(i=2;i<=length;i++)
{
x=r[i];
low=1;high=i-1;
while(low<=high)
{ mid=(low+high)/2;
if(x.key<r[mid].key) high=mid-1;
else low=mid+1;
}
for(j=i-1;j>=low;--j) r[j+1]=r[j];
r[low]=x;
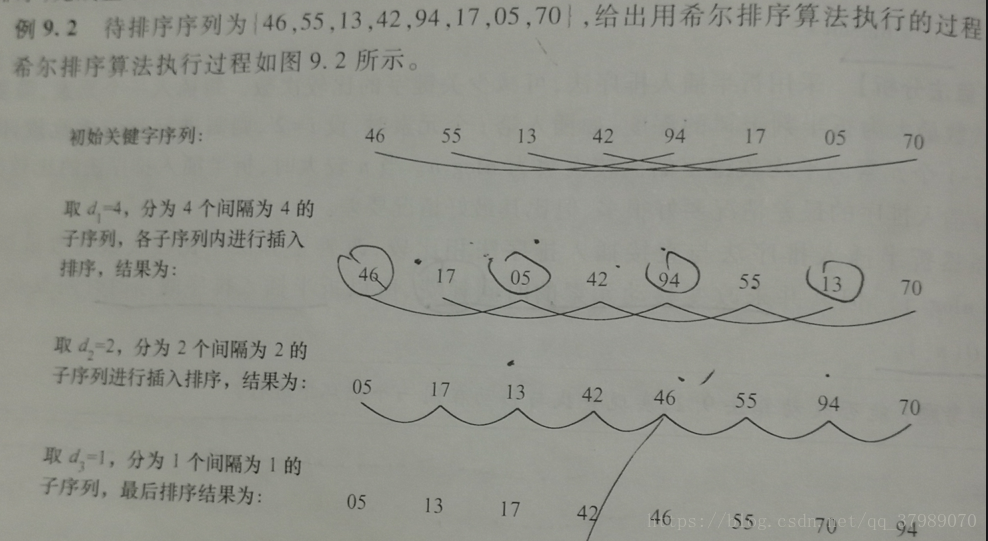
}}希爾排序: 時間複雜度O(n^1.5) 空間複雜度O(1)
void ShellInsert(RecordType r[],int length,int delta)
{
for(i=1+delta;i<=length;i++)
if(r[i].key<r[i-delta].key)
{
r[0]=r[i];
for(j=i-delta;j>0&&r[0].key<r[j].key;j-=delta)
r[j+delta]=r[j];
r[j+delta]=r[0];
}
}
void ShellSort(RecordType r[],int length,int delta[],int n)
{ /*length為陣列r長度,delta為新增陣列,n為delta[]長度*/
for(i=0;i<=n-1;++i)
ShellInsert(r,Length,delta[i]);
}2.交換類排序
氣泡排序: 時間複雜度O(n^2) 空間複雜度O(1) 穩定
void BubbleSort(RecordType r[],int n)
{
change=TRUE;
for(i=1;i<n-1&&change;++j)
{
change=FALSE;
for(j=1;j<=n-i;++j)
if(r[j].key>r[j+1].key)
{ x=r[j]; r[j]=r[j+1]; r[j+1]=x;
change=TRUE;
}
}
}序列 {48,62,35,77,55,14,35,98,22,40}進行氣泡排序
第一趟 48 35 62 55 14 35 77 22 40 98
第二趟 35 48 55 14 35 62 22 40 77 98
第三趟 35 48 14 35 55 22 40 62 77 98
第四趟 35 14 35 48 22 40 55 62 77 98
第五趟 14 35 35 22 40 48 55 62 77 98
第六趟 14 35 22 35 40 48 55 62 77 98
第七趟 14 22 35 35 40 48 55 62 77 98
快速排序: 時間複雜度 nlog2(n) 空間複雜度 log2(n) 不穩定
void QKSort(RecordType r[],int low,int high)
{
if(low<high)
{
pos=QKPass(r,low,high);
QKSort(r,low,pos-1);
QKSort(r,pos+1,high)
}
}
int QKPass(RecordType r[],int low,int high)
{
x=r[low];
while(low<high)
{
while(low<high&&r[high].key>=x.key)
high--;
if(low<high) {r[low]=r[high];low++;}
while(low<high&&r[low].key<x.key)
low++;
if(low<high) {r[high]=r[low];high--;}
}
r[low]=x;
}3.選擇類排序
簡單選擇排序: 時間複雜度O(n^2) 空間複雜度O(1) 不穩定
void SelectSort(RecordType r[],int n)
{
for(i=1;i<=n-1;++i)
{
k=i;
for(j=i+1;j<=n;++j)
if(r[j].key<r[k].key) k=j;
if(k!=i)
{x=r[i];r[i]=r[k];r[k]=x;}
}
}{48 62 35 77 55 14 35 98 }
14 {62 35 77 55 48 35 98 }
14 35 {62 77 55 48 35 98 }
14 35 35 {77 55 48 62 98}
14 35 35 48 {55 77 62 98}
14 35 35 48 55 62 77 98
樹形選擇排序: 時間複雜度:O(nlog2(n)) 空間複雜度O(n) 穩定
堆排序: 時間複雜度 O(nlog2(n)) 空間複雜度O(1) 不穩定
void sift(RecordType r[],int k,int m)
{ /*以r[k]為根的完全二叉樹,分別以r[2k]和r[2k+1]為根的左右子樹*/
t=r[k]; x=r[k].key; i=k; j=2*j;
finished=FALSE;
while(j<=m&&!finished)
{
if(j+1<=m&&r[j].key<r[j+1].key) j=j+1;
if(x>=r[j].key) finished=TRUE;
else
{r[i]=r[j];i=j;j=2*i;}
}
r[i]=t;
}
void crt_heap(RecordType r[],int n)
{
for(i=n/2;i>=1;--i)
sift(r,i,n);
}
void HeapSort(RecordType r[], int n)
{
crt_heap(r,n);
for(i=n;i>=2;--i)
{
b=r[1]; r[1]=r[i]; r[i]=b;
sift(r,1,i-1);
}
}
4.歸併排序
歸併排序:將兩個或者以上的有序表合併成一個新的有序表 時間複雜度O(nlog2(n)) 空間複雜度O(n) 穩定
5.分配類排序
多關鍵字排序
鏈式基數排序: O(d(n+rd)) O(rd) 穩定