求兩條空間直線的最近距離,以及他們最近距離線的兩點座標
設有兩空間線段
-
Ls,其起點、終點座標為s0、s1,方向向量u⃗ =s1−s0
-
Lt,其起點、終點座標為t0、t1,方向向量v⃗ =t1−t0 記兩線段對應的直線為ls、lt,採用向量表示法如下:
ls=s0+cs⋅u⃗
lt=t0+ct⋅v⃗ 當0≤cs、ct≤1時,上述兩式表達 設最短距離兩點分別為sj、tj,則有
sj=s0+sc⋅u⃗
tj=t0+sc⋅v⃗ 其中sc、tc為sj、tj兩點所對應的標量。
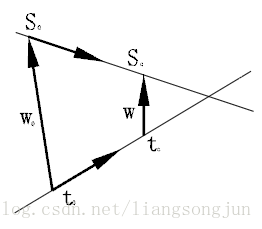
記向量w⃗ =sj−tj,記向量w⃗ 0=s0−t0,根據下圖可以得出:
w⃗ =s0+sc⋅u⃗ −(t0+tc⋅v⃗ )
即:
w⃗ =w⃗ 0+sc⋅u⃗ −tc⋅v⃗ (公式1) 如果s、t兩條直線不平行、重合,則存在唯一的兩點sc、tc使線段sctc−→−為ls、lt最近兩點的連線。同時,線段sctc−→−也是唯一與兩條直線同時垂直的線段。轉換為向量表達即為:
u⃗ ⋅w⃗ =0v⃗ ⋅w⃗ =0 將公式1代入上述兩式可得
(u⃗ ⋅u⃗ )sc−(u⃗ ⋅v⃗ )tc=−u⃗ ⋅w⃗ 0(公式2)
(v⃗ ⋅u⃗ )sc−(v⃗ ⋅v⃗ )tc=−v⃗ ⋅w⃗ 0(公式3) 記a=u⃗ ⋅u⃗ ,b=u⃗ ⋅v⃗ ,c=v⃗ ⋅v⃗ ,d=u⃗ ⋅w⃗ 0,e=v⃗ ⋅w⃗ 0,代入上述方程則可得:
sc=be−cdac−b2(公式4)
tc=ae−bdac−b2(公式5)
注意到上式中分母:
ac−b2=u⃗ ⋅u⃗ ×v⃗ ⋅v⃗ −(u⃗ ⋅v⃗ )2
⇒ac−b2=|u⃗ |2⋅|v⃗ |2−(|u⃗ |⋅|v⃗ |⋅cosq)2=(|u⃗ |⋅|v⃗ |⋅sinq)2≥0
當ac−b2=0時,公式2和公式3相互獨立,則兩直線平行,直線間的距離為一常數,我們可以在任意一條直線上指定一固定點,然後代入公式求距離。我們可以指定sc=0然後可以求得tc=db=ec。 當求出sc、tc我們即可求得sj、tj兩點,則兩點之間的距離可按下式求解:
d(ls,lt)=|sj−tj|=|s0−t0+(be−cd)u⃗ −(ae−bd)v⃗ ac−b2|
相關程式碼:
public class LineALineComputeIn3D { double PonA_x;//兩直線最近點之A線上的點的x座標 double PonA_y;//兩直線最近點之A線上的點的y座標 double PonA_z;//兩直線最近點之A線上的點的z座標 double PonB_x;//兩直線最近點之B線上的點的x座標 double PonB_y;//兩直線最近點之B線上的點的y座標 double PonB_z;//兩直線最近點之B線上的點的z座標 double distance;//兩直線距離
//直線A的第一個點 double a1_x ; double a1_y ; double a1_z ; //直線A的第二個點 double a2_x ; double a2_y ; double a2_z ;
//直線B的第一個點 double b1_x; double b1_y ; double b1_z ;
//直線B的第二個點 double b2_x; double b2_y ; double b2_z ; boolean bIsCompute=false;
//輸入直線A的兩個點,以便獲得A的方程 public void SetLineA(double A1x, double A1y, double A1z, double A2x, double A2y, double A2z) { a1_x = A1x; a1_y = A1y; a1_z = A1z;
a2_x = A2x; a2_y = A2y; a2_z = A2z; bIsCompute=false; }
//輸入直線B的兩個點,以便獲得B的方程 public void SetLineB(double B1x, double B1y, double B1z, double B2x, double B2y, double B2z) { b1_x = B1x; b1_y = B1y; b1_z = B1z;
b2_x = B2x; b2_y = B2y; b2_z = B2z; bIsCompute=false; }
//獲取A線上最近點 public double[] GetThePointInLineA() { double[] value=new double[3]; if(!bIsCompute){ StartCompute(); } value[0]=PonA_x; value[1]=PonA_y; value[2]=PonA_z; return value; }
//獲取A線上最近點 public double[] GetThePointInLineB() { double[] value=new double[3]; if(!bIsCompute){ StartCompute(); } value[0]=PonB_x; value[1]=PonB_y; value[2]=PonB_z; return value; } //獲取兩空間直線的最近距離 public double GetTwoLineDistance(){ if(!bIsCompute){ StartCompute(); } return distance; }
//用SetLineA、SetLineB輸入A、B方程後 //呼叫本函式解出結果 public void StartCompute() { //方法來自:http://blog.csdn.net/pi9nc/article/details/11820545
double d1_x = a2_x - a1_x; double d1_y = a2_y - a1_y; double d1_z = a2_z - a1_z;
double d2_x = b2_x - b1_x; double d2_y = b2_y - b1_y; double d2_z = b2_z - b1_z;
double e_x = b1_x - a1_x; double e_y = b1_y - a1_y; double e_z = b1_z - a1_z;
double cross_e_d2_x=0, cross_e_d2_y=0, cross_e_d2_z=0; double[] d2= cross(e_x, e_y, e_z, d2_x, d2_y, d2_z); cross_e_d2_x=d2[0]; cross_e_d2_y=d2[1]; cross_e_d2_z=d2[2]; double cross_e_d1_x, cross_e_d1_y, cross_e_d1_z; double[] d1= cross(e_x, e_y, e_z, d1_x, d1_y, d1_z); cross_e_d1_x=d1[0]; cross_e_d1_y=d1[1]; cross_e_d1_z=d1[2]; double cross_d1_d2_x, cross_d1_d2_y, cross_d1_d2_z; double[] d1d2= cross(d1_x, d1_y, d1_z, d2_x, d2_y, d2_z); cross_d1_d2_x=d1d2[0]; cross_d1_d2_y=d1d2[1]; cross_d1_d2_z=d1d2[2];
double t1=0, t2=0; t1 = dot(cross_e_d2_x, cross_e_d2_y, cross_e_d2_z, cross_d1_d2_x, cross_d1_d2_y, cross_d1_d2_z); t2 = dot(cross_e_d1_x, cross_e_d1_y, cross_e_d1_z, cross_d1_d2_x, cross_d1_d2_y, cross_d1_d2_z); double dd = norm(cross_d1_d2_x, cross_d1_d2_y, cross_d1_d2_z); t1 /= dd*dd;//複合賦值運算子,把左邊的變數除於右邊變數的值賦予右邊的變數,例如:a/=b等價於a=a/b t2 /= dd*dd;
//得到最近的位置 PonA_x = (a1_x + (a2_x - a1_x)*t1); PonA_y = (a1_y + (a2_y - a1_y)*t1); PonA_z = (a1_z + (a2_z - a1_z)*t1);
PonB_x = (b1_x + (b2_x - b1_x)*t2); PonB_y = (b1_y + (b2_y - b1_y)*t2); PonB_z = (b1_z + (b2_z - b1_z)*t2);
distance = norm(PonB_x - PonA_x, PonB_y - PonA_y, PonB_z - PonA_z); }
//點乘 double dot(double ax, double ay, double az, double bx, double by, double bz) { return ax*bx + ay*by + az*bz; }
//向量叉乘得到法向量 double[] cross(double ax, double ay, double az, double bx, double by, double bz) { double[] value=new double[3]; double x = ay*bz - az*by; double y = az*bx - ax*bz; double z = ax*by - ay*bx; value[0]=x; value[1]=y; value[2]=z; return value; }
//向量取模 double norm(double ax, double ay, double az) { return Math.sqrt(dot(ax, ay, az, ax, ay, az)); } }