bold source 頂點 路由 偽代碼 font 端點 -a 自底向上

單源最短路徑

給定一個圖,和一個源頂點src,找到從src到其它所有所有頂點的最短路徑，圖中可能含有負權值的邊。

Dijksra的算法是一個貪婪算法,時間復雜度是O(VLogV)(使用最小堆)。但是迪傑斯特拉算法在有負權值邊的圖中不適用,Bellman-Ford適合這樣的圖。在網絡路由中，該算法會被用作距離向量路由算法。Bellman-Ford也比迪傑斯特拉算法更簡單。但Bellman-Ford的時間復雜度是O(VE),這要比迪傑斯特拉算法慢。（V為頂點的個數,E為邊的個數）

算法描述

輸入:圖 和 源頂點
輸出:從src到所有頂點的最短距離。如果有負權回路(不是負權值的邊),則不計算該最短距離，沒有意義，因為可以穿越負權回路任意次，則最終為負無窮。

算法步驟

1.初始化：將除源點外的所有頂點的最短距離估計值 dist[v] ← +∞, dist[s] ←0;
2.叠代求解：反復對邊集E中的每條邊進行松弛操作，使得頂點集V中的每個頂點v的最短距離估計值逐步逼近其最短距離；（運行|v|-1次）
3.檢驗負權回路：判斷邊集E中的每一條邊的兩個端點是否收斂。如果存在未收斂的頂點，則算法返回false，表明問題無解；否則算法返回true，並且從源點可達的頂點v的最短距離保存在 dist[v]中。

關於該算法的證明也比較簡單，采用反證法，具體參考：http://courses.csail.mit.edu/6.006/spring11/lectures/lec15.pdf
該算法是利用動態規劃

的思想。該算法以自底向上的方式計算最短路徑。
它首先計算最多一條邊時的最短路徑(對於所有頂點)。然後,計算最多兩條邊時的最短路徑。外層循環需要執行|V|-1次。

例子

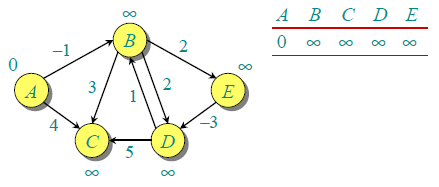
一下面的有向圖為例：給定源頂點是0，初始化源頂點距離所有的頂點都是是無窮大的,除了源頂點本身。因為有5個頂點，因此所有的邊需要處理4次。

按照以下的順序處理所有的邊：(B,E), (D,B), (B,D), (A,B), (A,C), (D,C), (B,C), (E,D).
第一次叠代得到如下的結果(第一行為初始化情況,最後一行為最終結果)：

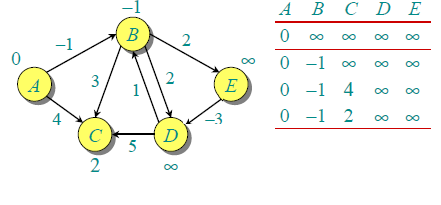
當 (B,E), (D,B), (B,D) 和 (A,B) 處理完後，得到的是第二行的結果。
當 (A,C) 處理完後，得到的是第三行的結果。
當 (D,C), (B,C) 和 (E,D) 處理完後，得到第四行的結果。

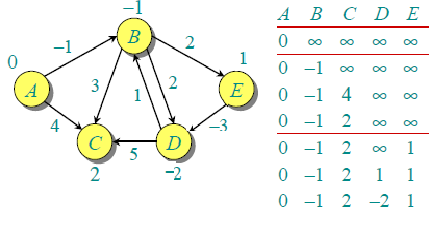
第一次叠代保證給所有最短路徑最多只有1條邊。當所有的邊被第二次處理後，得到如下的結果(最後一行為最終結果)：

第二次叠代保證給所有最短路徑最多只有2條邊。我們還需要2次叠代(即所謂的松弛操作)，就可以得到最終結果。

算法描述

1,.初始化：將除源點外的所有頂點的最短距離估計值 d[v] ——>+∞, d[s]——>0; 2.叠代求解：反復對邊集E中的每條邊進行松弛操作，使得頂點集V中的每個頂點v的最短距離估計值逐步逼近其最短距離；（運行|v|-1次） 3.檢驗負權回路：判斷邊集E中的每一條邊的兩個端點是否收斂。如果存在未收斂的頂點，則算法返回false，表明問題無解；否則算法返回true，並且從源點可達的頂點v的最短距離保存在 d[v]中。

為什麽要循環V-1次？
答：因為最短路徑肯定是個簡單路徑，不可能包含回路的，如果包含回路，且回路的權值和為正的，那麽去掉這個回路，可以得到更短的路徑如果回路的權值是負的，那麽肯定沒有解了.圖有n個點，又不能有回路，所以最短路徑最多n-1邊。又因為每次循環，至少relax一邊所以最多n-1次就行了。

算法導論上的偽代碼：

BELLMAN-FORD(G, w, s)
1  INITIALIZE-SINGLE-SOURCE(G, s)
2  for i ← 1 to |V[G]| - 1
3       do for each edge (u, v) ∈ E[G]
4              do RELAX(u, v, w)
5  for each edge (u, v) ∈ E[G]
6       do if d[v] > d[u] + w(u, v)
7             then return FALSE
8  return TRUE

Bellman-Ford算法——為什麽要循環V-1次？圖有n個點，又不能有回路，所以最短路徑最多n-1邊。又因為每次循環，至少relax一邊所以最多n-1次就行了！