動態規劃法之最長公共子串和最優二叉查詢樹
1. 筆試常考的題型,最長公共子串問題:給定兩個字串str1和str2,返回兩個字串的最長公共子串(連續)和長度。
舉例: str1 = "abc" str2="caba" 它們的最長公共子串是 "ab"。
此題可用暴力法進行求解,求解的時間複雜度較高。現用動態規劃法進行求解。
思想:如果 str1 的長度為 n,str2 的長度為 m,生成大小為 n*m 的 陣列矩陣 dp , dp[i][j]表示 str1[0…i] 與 str2[0…j] 的
最長公共子串的長度。
計算dp[i][j] 的方法一如下:
1)矩陣 dp 的第一列 dp[0…m-1][0].對於 某個位置(i,0)如果str1[i]==str2[0],則dp[i][0]=1,否則dp[i][0]=0
2)矩陣 dp 的第一行 dp[0][0…n-1].對於 某個位置(0,j)如果str1[0]==str2[j],則dp[0][j]=1,否則dp[0][j]=0
3)其他位置從左到右從上到下計算,dp[i][j]的值只有兩種情況:
當str1[i]==str2[j]時,dp[i][j]=dp[i-1][j-1]+1;
當str1[i]!=str2[j]則dp[i][j]=0。
圖示如下:
Java程式碼實現,請參考getMaxSubString1()。
解法二:經典動態規劃的方法需要大小為m*n的 dp 矩陣,空間複雜度可以減少至O(1),因為計算每一個dp[i][j]時只需計算dp[i-1][j-1],按照斜線方向計算所有的值,只需要一個變數即可。Java程式碼實現,請參考getMaxSubString2()。
package ExamTest; /*用例: abcdefghi bcdabefghijk 結果: 方法一:efghi 5 方法二:efghi 5 */ import java.util.Scanner; public class MaxSubString { public static void main(String[] args) { Scanner reader = new Scanner(System.in); String str = reader.nextLine(); String[] strs = str.split(" "); String strs1 = strs[0]; String strs2 = strs[1]; char[] str1 = strs1.toCharArray(); char[] str2 = strs2.toCharArray(); getMaxSubString1(str1,str2); getMaxSubString2(str1,str2); } public static void getMaxSubString1(char[] str1,char[] str2) { int dp[][]=new int[str2.length][str1.length]; //對dp矩陣的第一行賦值 for(int i=0;i<str1.length;i++) { if(str2[0]==str1[i]) { dp[0][i]=1; } else { dp[0][i]=0; } } //對dp矩陣的第一列賦值 for(int j=1;j<str2.length;j++) { if(str1[0]==str2[j]) { dp[j][0]=1; } else { dp[j][0]=0; } } for(int i=1;i<str2.length;i++)//將str2中各元素作為行元素與str1各元素進行比對 { for (int j=1;j<str1.length;j++)//將str1各元素與str2對應元素進行比對 { if (str1[j] == str2[i]) { dp[i][j] = dp[i - 1][j - 1] + 1; } else { dp[i][j] = 0; } } } int max=dp[0][0]; for(int i=0;i<str2.length;i++) { for (int j=0; j<str1.length;j++) { max = Math.max(max, dp[i][j]); } } System.out.println(max); } public static void getMaxSubString2(char[] str1,char[] str2) { int row = 0,len = 0,max = 0; int col = str1.length-1;//將str1作為列,str2作為行 while(row<str2.length) //每行進行比對判斷 { int i = row; int j = col; while(i<str2.length && j<str1.length)//按列從後往前判斷兩個字串陣列的值是否相等 { if(str2[i] == str1[j]) { len++; max = Math.max(max,len); } else { len = 0; } i++; j++; } if(col > 0) //如果這一列有元素沒有比對完成,本列繼續往前判斷. { col--; } else //一列比對完成,下移一行 { row++; } } System.out.println(max); } }
2. 最優二叉查詢樹(動態規劃法)
問題引入及描述:
•在電腦科學中,二叉查詢樹是最重要的資料結構之一。它的一種最主要應用是實現字典,這是一種具有查詢、插入和刪除操作的元素集合。如果集合中元素的查詢概率已知,這就很自然地引出了一個最優二叉查詢樹(BST)的問題:它在查詢中的平均鍵值比較次數是最低的。
•n個鍵{a1,a2,a3......an},其相應的查詢概率為{p1,p2,p3......pn}。構成最優BST,表示為T1n ,求這棵樹的平均查詢次數C[1, n](耗費最低)。即:如何構造這棵最優BST,使得C[1, n] 最小。
動態規劃求解過程:
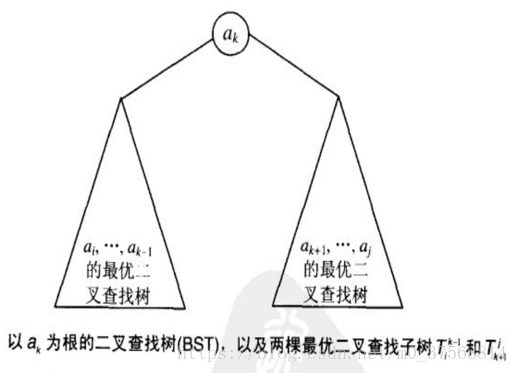
•從中選擇一個鍵ak作根節點,它的左子樹為T(i)k-1,右子樹為T(k+1)j。要求選擇的k 使得整棵樹的平均查詢次數C[i, j]最小。左右子樹遞迴執行此過程。
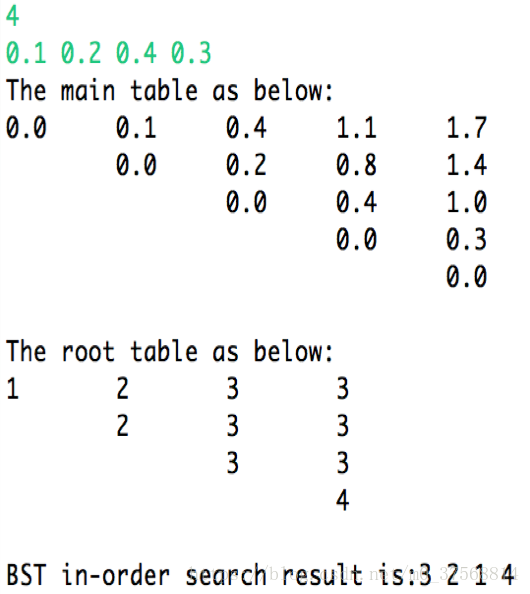
考慮分別以概率0.1,0.2,0.4,0.3來查詢4個鍵A,B,C,D 求成功查詢時,最優平均鍵值比較次數。
Java程式碼如下:
package ExamTest;
import java.util.Scanner;
/**
* Created by ZhangAnmy on 18/9/15.
* 輸入:一個n個鍵的有序列表的查詢概率陣列prop[1..n]
* 輸出:在最優BST中成功查詢的平均比較次數,以及最優BST中子樹的根表rTable
*/
public class OptimalBST {
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int num = sc.nextInt();
float[] prop = new float[num+1];
float[][] cTable = new float[num+2][num+1];
int[][] rTable = new int[num+2][num+1];
for(int i=1;i<=num;i++)
{
prop[i]=sc.nextFloat();
}
optFunc(num,cTable,prop,rTable);//呼叫動態規劃方法,求最優二叉查詢樹
print(num,cTable,rTable);//列印主表和最優根表
System.out.print("BST in-order search result is:");
OptimalBSTPrint(1,num,rTable);
}
public static void optFunc(int num,float cTable[][],float prop[],int rTable[][])
{
for(int i=1;i<=num;i++)//主表和根表元素的初始化
{
cTable[i][i-1]=0;
cTable[i][i]=prop[i];
rTable[i][i]=i;
}
cTable[num+1][num]=0;
int d = 0,kmin = -1,k,i,j,s;
float minval=9999,sum=0,temp;
for(d=1;d<=num-1;d++)
{
for(i=1;i<=num-d;i++)
{
j = i+d;
temp=minval;
for(k=i;k<=j;k++)//找最優根
{
if(cTable[i][k-1]+cTable[k+1][j]<temp)
{
temp= cTable[i][k-1]+cTable[k+1][j];
kmin = k;
}
}
rTable[i][j]= kmin;//將最優根記錄在根表對應位置中
sum=prop[i];
for(s=i+1;s<=j;s++)
{
sum = sum+prop[s];
}
cTable[i][j]=temp+sum;//主表中對應的最優值
}
}
}
public static void print(int num,float cTable[][],int rTable[][])
{
System.out.println("The main table as below:");
String s ="";
for(int i=1;i<=num+1;i++)
{
s=s+"\t";
for(int j=i-1;j<=num;j++)
{
float x = (float)(Math.round(cTable[i][j]*100))/100;//保留小數點後兩位
System.out.print(x+"\t");
// System.out.print(String.format("%.2f",cTable[i][j])+"\t"); //兩種方式均可
}
System.out.println();
System.out.print(s);
}
System.out.println();
System.out.println("The root table as below:");
s="";
for(int i=1;i<=num;i++)
{
s=s+"\t";
for(int j=i;j<=num;j++)
{
System.out.print(rTable[i][j]+"\t");
}
System.out.println();
System.out.print(s);
}
System.out.println();
}
//採用遞迴方式實現rTable[i][j]中最優根的輸出
public static void OptimalBSTPrint(int first,int last,int rTable[][])
{
int k;
if(first<=last)
{
k=rTable[first][last];
System.out.print(k+" ");
OptimalBSTPrint(first,k-1,rTable);
OptimalBSTPrint(k+1,last,rTable);
}
}
}
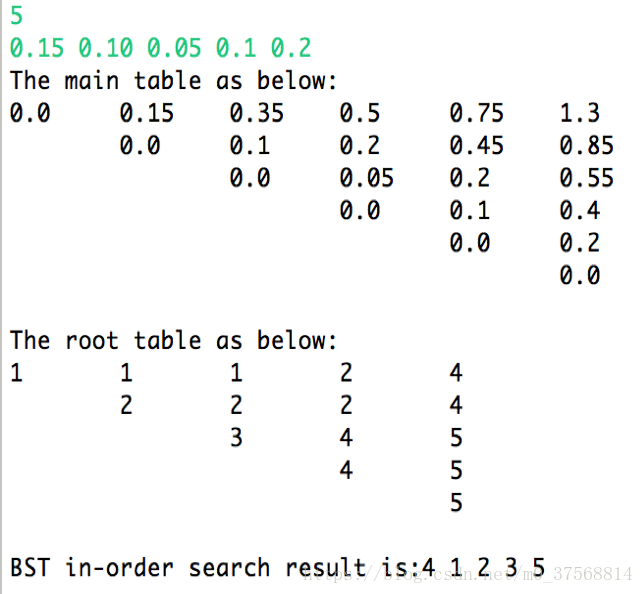
執行結果: