本系列同步釋出於本人的知乎專欄：確定性隨機

最新想開始再系統學習一次數理統計和隨機過程方便的知識，但是耽擱了一段時間，主要原因是不知道從哪裡開始。最近，剛好在網上“隨機”地買了一本《隨機模擬方法與應用》（肖柳青&周石鵬 編著），於是就決定從這本書開始吧。

給自己一個目標：看看自己能不能完整地些一個系列的讀書筆記。

1. 隨機模擬可以解決什麼樣的問題

在現實生活中，我們面對的很對問題都帶有隨機性，解決這類問題要使用能處理隨機性特徵的數學工具——概率與數理統計。用概率論來描述隨機系統的特徵有一個很大的缺陷：很多用於描述系統特徵的概率模型的求解十分困難，除極少數情況外很難獲得到數學上的解析解。

隨機模擬則通過對系統進行模擬，獲取系統的狀態變化和輸出結果的資料。通過大量隨機試驗，獲取並分析資料，在可接受的誤差範圍內估算系統行為的關鍵特徵量。計算機是目前進行隨機模擬的重要工具。

隨機模擬對數學的要求相對較低，且模擬的過程簡單且直觀，能夠讓人很直觀地瞭解系統行為的過程與結果。很多的數學模型是無法通過數學來直接求出它的解，它們只是描述了客觀世界的邏輯關係（但這樣也稱為數學模型）。

2. 隨機模擬的步驟

一個隨機模擬的步驟一般分為以下幾步：

（1） 確定描述系統狀態的變數。清楚說明被模擬的系統情況，包括：輸入、狀態和輸出，發生隨機的條件是什麼？這裡的系統有必要對現實情況進行一定的簡化；

（2） 設定變數。為系統的輸入、狀態和輸出系統設定變數，被設定某種型別的隨機數對應於隨機事件；

（3） 執行規則。寫出系統執行的基本邏輯，系統狀態是如何變化的，即狀態是如何更新的，那種型別的隨機數是如何產生的；

（4）模擬系統。給定系統的初始狀態，通過模擬系統的執行，給出系統的輸出；

（5）抽樣與統計。大量重複上述的隨機實驗，對結果進行統計，求出樣本的均值。至於進行多少次的模擬，基本要求是：大量地地重複實驗，直到要求出的結果穩定為止。

（6）對結果進行解析。對得到的結果進行模擬，必要的時候對前面的模擬過程進行修改並重新再進行一次，對結果進行比較。

隨機模擬關注的是對實際問題的解決，並非將關注點聚焦於數學問題的求解上。因此，隨機模擬的關鍵點是對實際問題的系統化建模描述，確定那些過程是通過隨機來實現。

3. 蒙提霍爾問題（Monty Hall Problem）

書中舉了好幾個用隨機模擬解決實際問題的例子，我這裡摘錄幾個有意思的，第一個就是所謂的蒙提霍爾問題（Monty Hall Problem）。所謂的蒙提霍爾問題，實際上是來自於一個美國的電視遊戲節目，這個結果的主持人就叫蒙提霍爾，因此才得此名。蒙提霍爾問題（這個電視結果的遊戲規則）的描述如下。

觀眾面對三扇門，其中有一扇門的後面有一輛汽車，另外兩扇後面各有一隻山羊。遊戲參與者可以從這三扇門中選擇其中一扇，若選擇的門後面是一輛汽車，則參賽者就可以贏得該汽車。一開始，當參賽者選定一扇門以後，主持人會從剩下的兩扇門中開啟其中一扇沒有汽車的門（但是有山羊），然後問參賽者要不要更換自己的選擇。這個問題的核心是參賽者更換自己的選擇是否會增加自己獲得汽車的概率？

首先，我們可以對這個問題進行一些基本分析。當參賽者選擇一扇門以後，他所選定的這扇門沒有汽車的概率是 ，其餘兩扇門有汽車的概率各為  。當主持人蒙提霍爾打開了一扇沒有汽車的門以後，另外一扇沒有被參賽者選中的門有汽車的概率變為  。所以，對參賽者而言，更改自己的選擇可以使得獲得汽車的概率從  提高到  ，概率提高了一倍。綜上分析，參賽者應該更換自己的選擇。

下面，根據隨機模擬的步驟解決這個問題。

首先，確定系統及系統的關鍵變數。

這個系統的輸入是參賽者的選擇，由於參賽者有兩個策略｛更換選擇，不更換選擇｝，猶豫者兩個策略是互斥的，因此我們只需要模擬一個即可。根據提幹，我們可以模擬當參賽者更換選擇時其能獲得汽車的概率。

其次，確定系統的執行規則。

由於參賽者是從三個門之間選擇，且只有一扇門有車。因此，我們可以隨機生成一個數  ，我們規定當  的時候表示參賽者選中了汽車。由於參賽者的策略  ，所以當一開始  時，其最終結果為沒選中，相反則參賽者最終獲得汽車。

再次，對系統進行模擬執行。

採取更換選擇策略，模擬的次數和最終能夠獲取到汽車的概率如下圖所示。

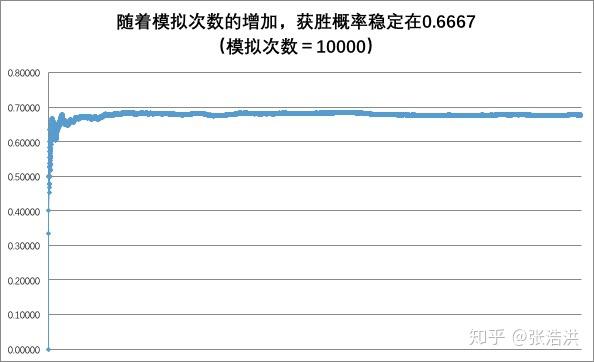
很明顯，隨著模擬次數的增加，參賽者在｛更換選擇｝這個策略下獲得汽車的概率穩定在0.667，也就是處。