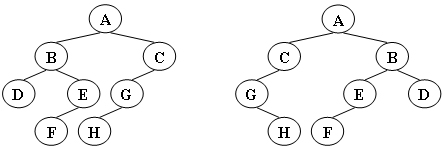
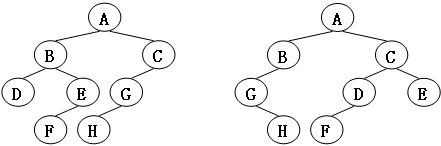
給定兩棵樹T1和T2。如果T1可以通過若干次左右孩子互換就變成T2，則我們稱兩棵樹是“同構”的。例如圖1給出的兩棵樹就是同構的，因為我們把其中一棵樹的結點A、B、G的左右孩子互換後，就得到另外一棵樹。而圖2就不是同構的。

圖1

圖2

現給定兩棵樹，請你判斷它們是否是同構的。

輸入格式:

輸入給出2棵二叉樹樹的資訊。對於每棵樹，首先在一行中給出一個非負整數N (≤10)，即該樹的結點數（此時假設結點從0到N−1編號）；隨後N行，第i行對應編號第i個結點，給出該結點中儲存的1個英文大寫字母、其左孩子結點的編號、右孩子結點的編號。如果孩子結點為空，則在相應位置上給出“-”。給出的資料間用一個空格分隔。注意：題目保證每個結點中儲存的字母是不同的。

輸出格式:

如果兩棵樹是同構的，輸出“Yes”，否則輸出“No”。

輸入樣例1（對應圖1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

輸出樣例1:

Yes

輸入樣例2（對應圖2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

輸出樣例2:

No

程式碼如下：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
int n1,n2;
const int maxn=15;
struct tree
{
    char data;
    int left,right;
};
int is1[maxn];
int is2[maxn];
tree t1[maxn];
tree t2[maxn];
int root1,root2;
void init()
{
    memset (is1,0,sizeof(is1));
    memset (is2,0,sizeof(is2));
}
void create (tree* t,int* is,int& n)
{
    scanf("%d",&n);
    getchar();
    for (int i=0;i<n;i++)
    {
        char l,r;
        scanf("%c %c %c",&t[i].data,&l,&r);
        getchar();
        if(l!='-')
        {
           int lnum=l-'0';
           t[i].left=lnum;
           is[lnum]=1;
        }
        else
            t[i].left=-1;
        if(r!='-')
        {
            int rnum=r-'0';
            t[i].right=rnum;
            is[rnum]=1;
        }
        else
            t[i].right=-1;
    }
}
void parent (tree* t,int& root,int* is,int& n)
{
    for (int i=0;i<n;i++)
        if(!is[i])
       {
           root=i;
           return;
       }
}
bool is_Same (int tt1,int tt2)
{
    if(tt1!=-1&&tt2!=-1&&t1[tt1].data==t2[tt2].data)
    {
        return (is_Same(t1[tt1].left,t2[tt2].left)&&is_Same(t1[tt1].right,t2[tt2].right))||(is_Same(t1[tt1].right,t2[tt2].left)&&is_Same(t1[tt1].left,t2[tt2].right));
    }
    else if(tt1==-1&&tt2==-1)
        return true;
    else
        return false;
}
int main()
{
    init();
    create(t1,is1,n1);
    create(t2,is2,n2);
    parent(t1,root1,is1,n1);
    parent(t2,root2,is2,n2);
    if(n1==0&&n2==0)
        printf("Yes\n");
    else if(n1!=n2)
        printf("No\n");
    else
        printf("%s\n",is_Same(root1,root2)==true? "Yes":"No");
    return 0;
}