[work] python中的除法,取整和求模
首先註明:如果沒有特別說明,以下內容都是基於python 3.4的。
先說核心要點:
1. /是精確除法,//是向下取整除法,%是求模
2. %求模是基於向下取整除法規則的
3. 四捨五入取整round, 向零取整int, 向下和向上取整函式math.floor, math.ceil
4. //和math.floor在CPython中的不同
5. /在python 2 中是向下取整運算
6. C中%是向零取整求模。
如果你對上面這幾點都很熟悉,那麼就不要浪費時間往下看了,珍惜生命,遠離氾濫的灌水文章!
大綱如下:
1. 一個測試程式和它的輸出
2. 取整和求模運算規則
3. python中其他的取整運算
4. //和math.floor在CPython中的不同
5. 運算子/在python 2 和python 3 中的區別
6. 其他討論(求餘和求模)
下面按順序介紹:
1. 一個測試程式和它的輸出
測試程式如下(python 3.4):
print('usage of 3 operators /, // and % in python 3.4') print('1). usage of /') print ('10/4 = ', 10/4) print ('-10/4 = ', -10/4) print ('10/-4 = ', 10/-4) print ('-10/-4 = ', -10/-4) print('\n2). usage of //') print ('10//4 = ', 10//4) print ('-10//4 = ', -10//4) print ('10//-4 = ', 10//-4) print ('-10//-4 = ', -10//-4) print('\n3). usage of %') print ('10%4 = ', 10%4) print ('-10%4 = ', -10%4) print ('10%-4 = ', 10%-4) print ('-10%-4 = ', -10%-4)
輸出結果如下:
usage of 3 operators /, // and % in python 3.4
1). usage of /
10/4 = 2.5
-10/4 = -2.5
10/-4 = -2.5
-10/-4 = 2.5
2). usage of //
10//4 = 2
-10//4 = -3
10//-4 = -3
-10//-4 = 2
3). usage of %
10%4 = 2
-10%4 = 2
10%-4 = -2
-10%-4 = -2如果被除數和除數都是正整數,比如10對4求模,一般人都能算出來是2,但是如果兩個或其中一個是負數,比如-10對4求模,取整除法和模應該如何計算呢?雖然我們可以從上面的輸出總結一個現象律:模和除數同號(除非能整除是模是0)
2.取整和求模運算規則
求模運算規則是由除法規則定的,因為被除數(dividend), 除數(divisor),商(quotient)和模(或餘數,modulus or remainder)在數學上必須滿足如下關係:
被除數=除數*商+模 (方程1)
變化一下,已知被除數和餘數,模可以通過商計算出來,計算公式如下:
模=被除數-除數*商 (方程2)
從wiki(https://en.wikipedia.org/wiki/Modulo_operation)查到三種不同的演算法,這裡拷貝了其中的一張圖(只有英文版)

圖1:三種不同的演算法 。圖中紅線表示商,綠線表示模。橫座標表示被除數,縱座標表示商或模。
這幅圖可以分成三行兩列,共6個子圖。三行trancated/floored/Euclidean division代表三種取整除法(下面會討論);兩列的解釋是:第一列positive divisor, 也就是說除數是正數,第二列negative divisor,除數是負數。那這幅圖到底是什麼意思呢? 現在拿第二行第一列的子圖解釋一下 (floored division, positive divisor),這裡的橫座標表示被除數,縱座標表示商或模。這個子圖中除數(divisor)是正數,當被除數也是正數時(比如前面討論的10對4求模),商和餘數都是正數或零;當被除數是負數的時候(比如之前討論的-10對4求模),採取了向下(負數方向)取整(rounded downwards, , 函式floor的功能),本來精確除法下答案是 (-10/4 = )-2.5,現在向下取整答案是(-10//4 =) -3,也就是取整後的結果(-3)必須小於等於精確結果(-2.5), 這時用商和模的關係(方程2)很容易計算出模是2, 這也是前面例子中討論的。這就是python採用的floored division演算法,這個演算法可以說是python的//和%運算符采用的最重要也是唯一的規則(當然還有abs(模) < abs(除數)),對所有的情況都適用(你可以仔細看看開始討論的測試程式和圖1中第二行的兩個子圖)。其它的現象都可以從這個規則中推匯出來。比如我們前面說的python模運算子%的一個現象規律:模要麼與除數同號,要麼是零(能整除的情況下)。其本質是由python採取的向下取整演算法決定的。我們只需要記住python的取整規則是:向下取整!向下取整!向下取整!
另外兩種:第一種truncated division,是向零取整,也就是簡單粗暴地去掉小數部分,C語言採用這種方法(例子見後面的討論)。還有一種是Euclidean division, 這裡不討論了,有興趣的同學可以問度娘或谷哥。
當然還有一種取整法,就是我們耳熟能詳的四捨五入法,:)。
下面接著介紹python中其它的取整方法。
3.python中其他的取整運算
首先說明,取整或模運算(比如a//b, a%b)中, a和b都可以是非整數,比如
-10.6//2.1=-6.0
-10.6//2.1=2.00000…
這也可以歸納到上面所說的向下取整規則中,當然還有一條隱蔽規則:模的絕對值小於除數的絕對值,也就是abs(模) < abs(除數)
python能夠實現基本的四種取整運算:四捨五入,向零取整,向下取整和向上取整。
四捨五入取整函式round
>>>round(3.5)
4
>>>round(-3.5)
-4
>>>round(3.49)
3
>>>round(-3.49)
-3向零取整函式int
>>>int(3.99)
3
>>>int (-3.99)
-3math模組中向下取整函式floor和向上取整函式ceil
>>>from math import floor, ceil
>>>floor(3.99)
3
>>>floor(-3.-1)
-4
>>>ceil(3.01)
4
>>>ceil(-3.99)
-34.//和math.floor在CPython中的不同
從以上討論中可以看出,//和math.floor對除法運算都是向下取整,結果應該相同,比如
>>>from math import floor
>>>3//5 == floor(3/5)
True但是
>>>1//0.05 == floor(1/0.05)
FalseWhat? 不是說好的相同嗎,友誼的小船怎麼說翻就翻呢?
分開測試:
>>> 1/0.05
20.0
>>> 1//0.05
19.0
>>> floor(1/0.05)
20先說結論:這個問題是由於cpython的向下取整除法運算子(//)的實現不是 浮點除法+floor 來實現而是用了(被除數 - 餘數)/除數 導致的。
PS:Jython下可以得到20.0,而PEP裡規定了a // b應該等於round(a/b),所以似乎這是cpython實現的一個bug?
首先先分析下1 / 0.05究竟應該等於多少。答案就是精確的20.0。簡單解釋下:IEEE754浮點數規定,如果一個浮點數的值不能被精確記錄,那麼它的值會被記成與這個數距離最近的可以被IEEE浮點數表示的數。首先,0.05在二進位制下是無限迴圈小數,自然不能被精確記錄,因此0.05這個浮點數的實際值是不等於0.05的,實際值是約為0.05 + 2.7e-18。之後做浮點除法,實際上做的是1 / (0.05+2.7…e-18),這個除法的結果大約是20 - 1.1e-15。這個值也不能被精確表示,恰好離這個數最近的可以表示的值就是20.0,因此即使有浮點數誤差結果也是精確的20.0。既然1/0.05就是20.0,那麼對他做floor運算自然也是20了。
現在的問題就是為什麼1 // 0.05會變成19.0,要解決這個問題只能翻原始碼看//運算子的實現。
這裡不貼原始碼了,結論是:cpython中x // y的實現實際上是round((x - fmod(x, y)) / y) ,其中fmod函式是求兩個浮點數相除的餘數。
這樣一來就解釋的通了:在十進位制下,顯然1除以0.05的餘數應該是0.0。然而在IEEE浮點數環境中,0.05的實際值是約0.05 + 2.7e-18,略大於0.05,這樣一來1除以這個數的餘數就成了約0.05 - 5e-17,從1中減掉這麼多之後就只剩0.95了,除以0.05再round後變成19.0。
注:這段主要參考知乎上的一篇文章(http://www.zhihu.com/question/41017093/answer/89848433),如有興趣,大家可檢視,裡面有原始碼。
5.運算子/在python 2 和python 3 中的區別
//和%運算子在2和3版本中一樣,但是運算子/不一樣,最開始的測試程式中和運算子/有關的部分在python 2.7中的輸出結果是這樣的:
print ('10/4 = ', 10/4)
print ('-10/4 = ', -10/4)
print ('10/-4 = ', 10/-4)
print ('-10/-4 = ', -10/-4)('1
輸出:
('10/4 = ', 2)
('-10/4 = ', -3)
('10/-4 = ', -3)
('-10/-4 = ', 2)除了大家熟知的print用法不一樣外,這裡要說的是運算子/在python 3以前的版本是向下取整(等同於//),這是大家要注意的。
6.其他討論(求餘和求模)
一篇文章(http://blog.sina.com.cn/s/blog_a3052b4a01018fd7.html)討論求餘和求模的區別 , 原文中列了一個表格,我拷貝在下面 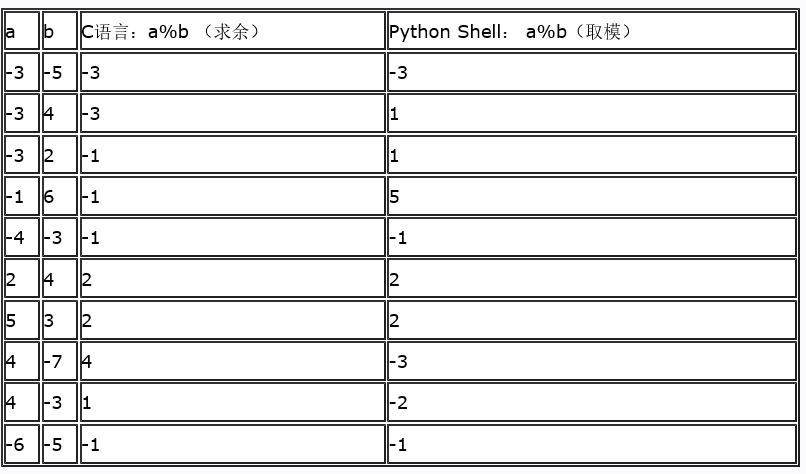
原作者認為: 取模運算時,向0 方向舍入(fix()函式); 求餘運算時,向無窮小方向舍入(floor()函式)。
還有一篇文章(http://www.cnblogs.com/xfzhang/archive/2010/11/25/1887214.html),討論在matlab中取模(mod)與取餘(rem)的不同。
不能說這些觀點本身有什麼錯誤,matlab 也確實給出了兩個不同的函式,細化了區別。但我卻認為這樣處理把問題複雜化了,我們沒有必要在文字上鑽牛角尖,非得人為區分“求餘”和”求模”。我們就可以簡單地認為兩者相同,比如統一用”求模” 表示(當然你也可以用“求餘”),只是在數學運算和不同程式語言中求模時存在不同的取整演算法,主要是上面討論的三種:truncated division, floored division, Euclidean division。 C語言用的是truncated division, 而python用的是floored division.
