劍指offer所有的題目總結
目錄
五、其他
9、連結串列迴文結構
基本都是參考別的部落格和書本的程式碼,僅作為自己筆記用!!
零、小結:
1、<< : 左移運算子,num << 1,相當於num乘以2
>> : 右移運算子,num >> 1,相當於num除以2
>>> : 無符號右移,忽略符號位,空位都以0補齊
2、//與1位與得1就是奇數,1只有最後一位是1
一、位運算
1、二進位制中1的個數
輸入一個整數,輸出該數二進位制表示中1的個數。其中負數用補碼錶示。
思路:最簡單的思路,整數n每次進行無符號右移一位,同1做&運算,可以判斷最後以為是否為1。
通常的劍指offer的思路,n&(n-1) 操作相當於把二進位制表示中最右邊的1變成0。所以只需要看看進行了多少次這樣的操作即可。看看什麼時候n為0.
public class erjinzhi { public int NumberOf1(int n) { /*int count = 0; //自己的思路,主要就是n與2 4 8 16分別與,來判斷 long temp = 1; for(int i = 1; i <= 32;i++){ if((n&temp) > 0) count++; temp = temp * 2; } return count;*/ /* //簡單的思路 int res = 0; while (n!=0) { res = res + n&1; n>>>=1; } return res;*/ int count = 0; while(n!=0) { n = n&(n-1); count++; } return count; } }
-
2、判斷二進位制中0的個數
思路:每次右移一位,判斷是否是0即可。暫時沒有找到別的好思路。
public static int findZero(int n) {
int count = 0;
while(n != 0) {
if((n&1)!=1)
count++;
n>>>=1;
}
return count;
}-
3.二進位制高位連續0的個數
思路:每次與最高位為1的二進位制進行&操作。0x80000000的二進位制是1000 0000 0000 0000 ...共32位,最高位為1.
參考https://blog.csdn.net/u013190513/article/details/70216730
https://www.cnblogs.com/hongten/p/hongten_java_integer_toBinaryString.html
https://blog.csdn.net/lpjishu/article/details/51323722
public static int numberOfLeadingZeros0(int i){
if(i == 0)
return 32;
int n = 0;
int mask = 0x80000000;
int j = i & mask;
while(j == 0){
n++;
i <<= 1;
j = i & mask;
}
return n;
}JDK中原始碼解決思路.
public static int numberOfLeadingZeros(int i) {
// HD, Figure 5-6
if (i == 0)
return 32;
int n = 1;
if (i >>> 16 == 0) { n += 16; i <<= 16; }
if (i >>> 24 == 0) { n += 8; i <<= 8; }
if (i >>> 28 == 0) { n += 4; i <<= 4; }
if (i >>> 30 == 0) { n += 2; i <<= 2; }
n -= i >>> 31;
return n;
}二、二叉樹
-
1、二叉搜尋樹第k個結點
給定一顆二叉搜尋樹,請找出其中的第k小的結點。例如, 5 / \ 3 7 /\ /\ 2 4 6 8 中,按結點數值大小順序第三個結點的值為4。
思路:遞迴的方式:二叉搜尋樹的中序遍歷就是排序的,所以用中序遍歷,每一次中間的時候判斷是否等於k即可。
非遞迴的方式:運用棧進行操作。相當於用棧實現了中序遍歷,在中間進行了個數的判斷
int count = 0;
TreeNode KthNode(TreeNode pRoot, int k)
{
if(pRoot != null) {
TreeNode leftNode = KthNode(pRoot.left, k);
if(leftNode != null)
return leftNode;
count++;
if(count == k)
return pRoot;
TreeNode rightNode = KthNode(pRoot.right, k);
if(rightNode != null)
return rightNode;
}
return null;
}//棧的方式
TreeNode KthNode(TreeNode pRoot, int k)
{
Stack<TreeNode> stack = new Stack<TreeNode>();
if(pRoot==null||k==0) return null;
int t=0;
while(pRoot!=null ||stack.size()>0){
while(pRoot!=null){
stack.push(pRoot);
pRoot = pRoot.left;
}
if(stack.size()>0){
pRoot= stack.pop();
t++;
if(t==k) return pRoot;
pRoot= pRoot.right;
}
}
return null;
}-
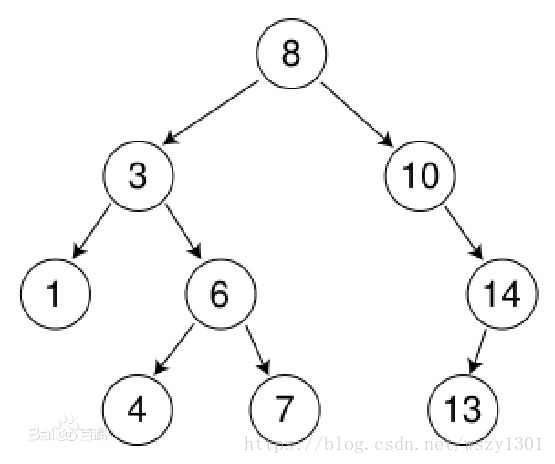
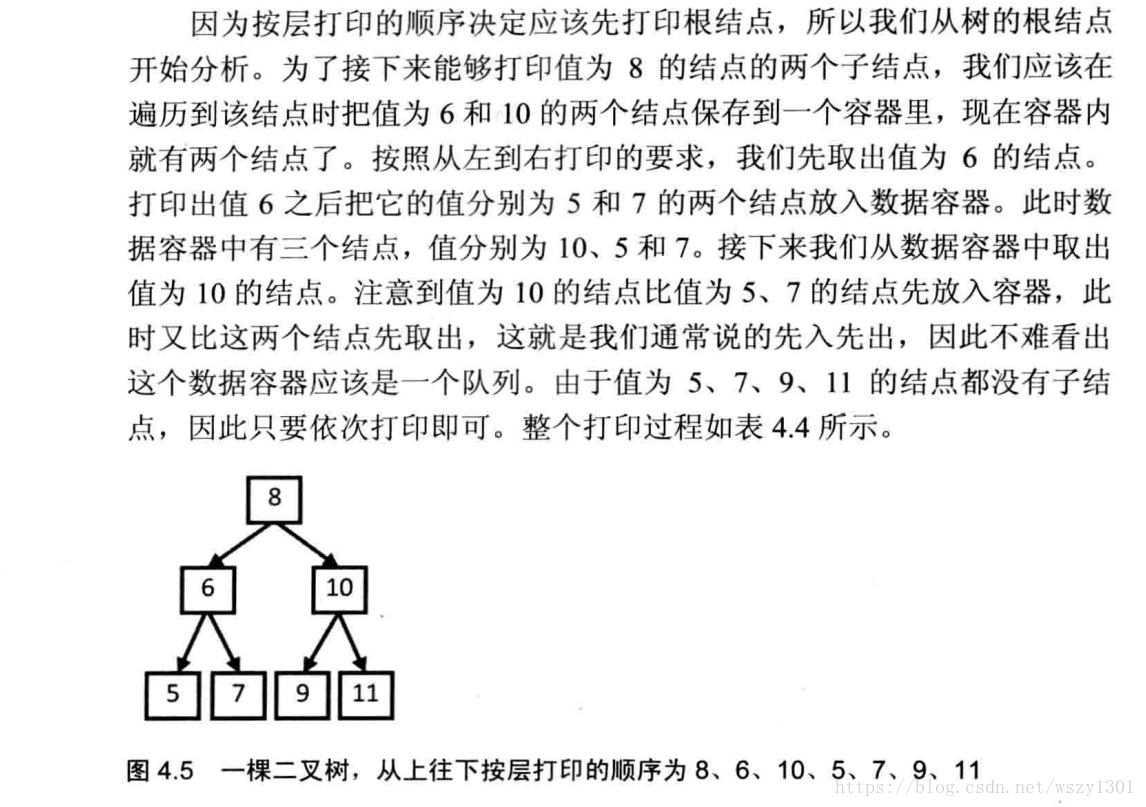
2.0 從上往下列印二叉樹
從上往下打印出二叉樹的每個節點,同層節點從左至右列印。
思路:
import java.util.ArrayList;
import java.util.LinkedList;
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
/**
* 演算法思路,(劍指offer圖片)
* 1.根節點放到佇列裡面,佇列不空,就列印佇列頭,列印這個節點,馬上把這個節點的左右子節點放到佇列中。
* 2.再要訪問一個節點,把這個節點的左右放入,此時隊頭是同層的,對位是打印出來的左右。依次先入先出就可以得到結果。
* @param root
* @return
*/
public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
ArrayList<Integer> layerList = new ArrayList<Integer>();
if (root == null)
return layerList;
LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
layerList.add(node.val);
if (node.left != null)
queue.addLast(node.left);
if (node.right != null)
queue.addLast(node.right);
}
return layerList;
}
}-
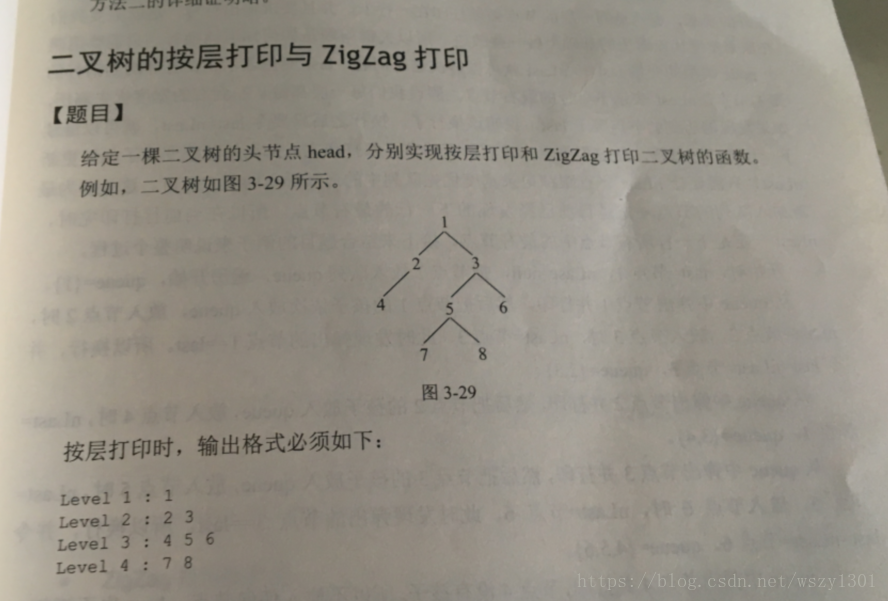
2.1二叉樹列印成多行
從上到下按層列印二叉樹,同一層結點從左至右輸出。每一層輸出一行。(注意是一行一行輸出)
思路:主要採用左程雲的思路,
static ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
if(pRoot == null)
return res;
Queue<TreeNode> queue = new LinkedList<TreeNode>();
TreeNode last = pRoot;
TreeNode nlast =null;
queue.offer(pRoot);
ArrayList<Integer> tmp = new ArrayList<>();
while (!queue.isEmpty()) {
pRoot = queue.poll();
tmp.add(pRoot.val);//出佇列,就把他左右孩子入佇列,
//此時,下一層的最右要跟著更新
if (pRoot.left!=null) {
queue.offer(pRoot.left);
nlast = pRoot.left;
}
if (pRoot.right!=null) {
queue.offer(pRoot.right);
nlast = pRoot.right;
}
//如果到了本層的最右,就把這一層結果放入。注意最後一層時,isempty不成立,
//最後一層的結果要單獨放入。
if (pRoot == last && !queue.isEmpty()) {
res.add(new ArrayList<>(tmp));
last = nlast;
tmp.clear();
}
}
res.add(new ArrayList<>(tmp));
return res;
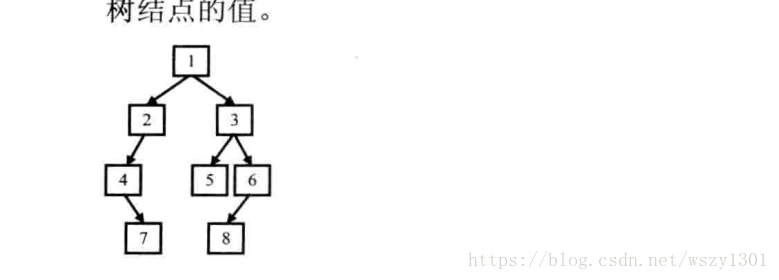
}2.2按之字形順序列印二叉樹
題目描述
請實現一個函式按照之字形列印二叉樹,即第一行按照從左到右的順序列印,第二層按照從右至左的順序列印,第三行按照從左到右的順序列印,其他行以此類推。
利用兩個棧的輔助空間分別儲存奇數偶數層的節點,然後列印輸出。或使用連結串列的輔助空間來實現,利用連結串列的反向迭實現逆序輸出。
import java.util.ArrayList;
import java.util.Stack;
/*
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
//利用兩個棧的輔助空間分別儲存奇數偶數層的節點,然後列印輸出。或使用連結串列的輔助空間來實現,利用連結串列的反向迭實現逆序輸出。
public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
if(pRoot == null)
return res;
Stack<TreeNode> s1 = new Stack<>();
Stack<TreeNode> s2 = new Stack<>();
s1.push(pRoot);
int level = 1;
while (!s1.empty()||!s2.empty()) {
if (level %2 != 0) {
ArrayList<Integer> list = new ArrayList<>();
while (!s1.empty()) {
TreeNode node = s1.pop();
if (node!= null) {
list.add(node.val);
s2.push(node.left);//因為偶數層,先右後左,所以要先放左子樹,棧
s2.push(node.right);
}
}
if (!list.isEmpty()) {
res.add(list);
level++;
}
}
else {
ArrayList<Integer> list = new ArrayList<>();
while (!s2.empty()) {
TreeNode node = s2.pop();
if (node!= null) {
list.add(node.val);
s1.push(node.right);
s1.push(node.left);
}
}
if (!list.isEmpty()) {
res.add(list);
level++;
}
}
}
return res;
}
}-
3.資料流中位數
如何得到一個數據流中的中位數?如果從資料流中讀出奇數個數值,那麼中位數就是所有數值排序之後位於中間的數值。如果從資料流中讀出偶數個數值,那麼中位數就是所有數值排序之後中間兩個數的平均值。
思路:主要是部落格的程式碼,參考了左的部分分析。
建立優先順序佇列維護大頂堆和小頂堆兩個堆,並且小頂堆的值都大於大頂堆的值。比如6,1,3,0,9,8,7,2則較小的部分大根堆是0,1,2,3 較大的部分小根堆是6,7,8,9.
具體思路:
1.本程式碼為了保證兩個堆的尺寸差距最大為1,採用奇數個時候插到大根堆,偶數個插到小根堆。
2.當資料總數為偶數時,新加入的元素,應當進入小根堆(注意不是直接進入小根堆,而是經大根堆篩選後取大根堆中最大元素進入小根堆),要保證小根堆裡面所有數都比大根堆的大。
3.當資料為奇數個時,按照相應的調整進入大根堆。
4.如果個數位奇數個,則大根堆堆頂為中位數,否則就是兩個堆頂除以2.比如新加入三個,那麼第一個在大,第二個在小,第三個可能在大。所以就是大根堆的堆頂。
* 插入有兩種思路: 左採用第一種,本程式碼採用第二種
* 1:直接插入大堆中,之後若兩堆尺寸之差大於1(也就是2),則從大堆中彈出堆頂元素並插入到小堆中
* 若兩隊之差不大於1,則直接插入大堆中即可。
* 2:奇數個數插入到大堆中,偶數個數插入到小堆中,
* 但是 可能會出現當前待插入的數比小堆堆頂元素大,此時需要將元素先插入到小堆,然後將小堆堆頂元素彈出並插入到大堆中
* 對於偶數時插入小堆的情況,一樣的道理。why?
* 因為要保證最大堆的元素要比最小堆的元素都要小。
import java.util.Comparator;
import java.util.PriorityQueue;
public class Shujuliumedian {
int count = 0;
PriorityQueue<Integer> minheap = new PriorityQueue<>();
PriorityQueue<Integer> maxheap = new PriorityQueue<>(11, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
// TODO Auto-generated method stub
return o2.compareTo(o1);//o2大於o1返回1 ,否則返回-1
}
});
public void Insert(Integer num) {
count++;
if (count % 2 ==0) {//偶數進入小根堆,這個其實無所謂,定了一個平均分配的規則
//保證進入小根堆的元素要比大根堆最大的大,所以如果小調整
if (!maxheap.isEmpty() && num < maxheap.peek()) {
maxheap.offer(num);
num = maxheap.poll();
}
minheap.offer(num);
}
else {//奇數進入大根堆
if (!minheap.isEmpty() && num > minheap.peek()) {
minheap.offer(num);
num = minheap.poll();
}
maxheap.offer(num);
}
}
public Double GetMedian() {
double median = 0;
if (count % 2 ==1) {
median = maxheap.peek();
}
else
median = (minheap.peek()+maxheap.peek())/2.0;
return median;
}
}
-
4.二叉樹中和為某一值的路徑
輸入一顆二叉樹的跟節點和一個整數,打印出二叉樹中結點值的和為輸入整數的所有路徑。路徑定義為從樹的根結點開始往下一直到葉結點所經過的結點形成一條路徑。(注意: 在返回值的list中,陣列長度大的陣列靠前)
思路: * 劍指offer思路 部落格程式碼
* 程式碼步驟:一個連結串列記錄路徑,一個存放這個連結串列的連結串列記錄最終的結果。
* 1.首先將根節點放入連結串列,target減去這個根節點
* 2.判斷是否target同時是葉子節點,如果是就將當前的連結串列放在結果連表裡
* 3.如果不是,就遞迴去訪問左右子節點。
* 4.無論是找到沒有,都要回退一步、
import java.util.ArrayList;
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
private ArrayList<ArrayList<Integer>> listAll = new ArrayList<ArrayList<Integer>>();
private ArrayList<Integer> list =new ArrayList<Integer>();
private ArrayList<ArrayList<Integer>> resultList = new ArrayList<ArrayList<Integer>>();
/**
* 劍指offer思路
* 程式碼步驟:一個連結串列記錄路徑,一個存放這個連結串列的連結串列記錄最終的結果。前序遍歷去訪問。先訪問根,在遞迴在左右子樹找。注意回退
* 1.首先將根節點放入連結串列,target減去這個根節點
* 2.判斷是否target同時是葉子節點,如果是就將當前的連結串列放在結果連表裡
* 3.如果不是,就遞迴去訪問左右子節點。
* 4.無論是找到沒有,都要回退一步、
* @param root
* @param target
* @return
*/
public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
if(root == null)
return resultList;
list.add(root.val);
target = target - root.val;
if(target == 0 && root.left == null && root.right == null){
resultList.add(new ArrayList<Integer>(list));
}
else {
FindPath(root.left, target);
FindPath(root.right, target);
}
// 在返回父節點之前,在路徑上刪除該結點
list.remove(list.size()-1);
return resultList;
}
}-
5.重建二叉樹
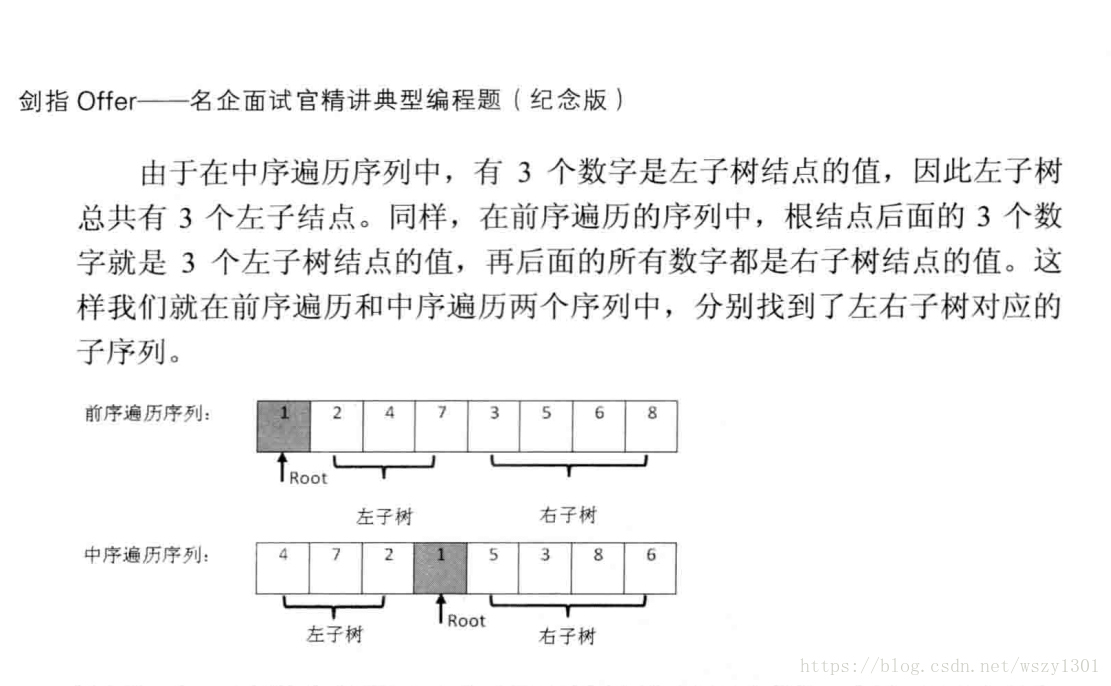
輸入某二叉樹的前序遍歷和中序遍歷的結果,請重建出該二叉樹。假設輸入的前序遍歷和中序遍歷的結果中都不含重複的數字。例如輸入前序遍歷序列{1,2,4,7,3,5,6,8}和中序遍歷序列{4,7,2,1,5,3,8,6},則重建二叉樹並返回。
思路:劍指
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
import java.util.Arrays;
public class Solution {
public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
if (pre == null || in == null) {
return null;
}
if (pre.length == 0 || in.length == 0) {
return null;
}
if (pre.length != in.length) {
return null;
}
TreeNode root = new TreeNode(pre[0]);//第一個
for (int i = 0; i < in.length; i++) {
if (pre[0] == in[i]) {
//pre的0往後數i個是左子樹的,copyofrange包含前面的下標,不包含後面的下標
//in的i往前數i個是左子樹的。
root.left = reConstructBinaryTree(Arrays.copyOfRange(pre, 1, i + 1), Arrays.copyOfRange(in, 0, i));
//注意in是從i+1開始,因為i是現在的根,i+1開始才是右子樹
root.right = reConstructBinaryTree(Arrays.copyOfRange(pre, i + 1, pre.length),
Arrays.copyOfRange(in, i + 1, in.length));
}
}
return root;
}
}-
6.樹的子結構
輸入兩棵二叉樹A,B,判斷B是不是A的子結構。(ps:我們約定空樹不是任意一個樹的子結構)
思路: //先從根開始再把左作為根,再把右作為根由本函式決定。把一個為根的時候的具體比對過程是第二個函式決定。
//從根可以認為是一顆樹,從左子樹開始又可以認為是另外一顆樹,從右子樹開始又是另外一棵樹。
//本函式就是判斷這一整顆樹包不包含樹2,如果從根開始的不包含,就從左子樹作為根節點開始判斷,
//再不包含從右子樹作為根節點開始判斷。
//是整體演算法遞迴流程控制。
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
//先從根開始再把左作為根,再把右作為根由本函式決定。把一個為根的時候的具體比對過程是第二個函式決定。
//從根可以認為是一顆樹,從左子樹開始又可以認為是另外一顆樹,從右子樹開始又是另外一棵樹。
//本函式就是判斷這一整顆樹包不包含樹2,如果從根開始的不包含,就從左子樹作為根節點開始判斷,
//再不包含從右子樹作為根節點開始判斷。
//是整體演算法遞迴流程控制。
public boolean HasSubtree(TreeNode root1,TreeNode root2) {
boolean res = false;
if (root1 != null && root2 != null) {
if(root1.val == root2.val){
res = doesTree1haveTree2(root1,root2);
}
if(!res)
{
res = HasSubtree(root1.left, root2);
}
if(!res)
{
res = HasSubtree(root1.right, root2);
}
}
return res;
}
//本函式,判斷從當前的節點 ,開始兩個樹能不能對應上,是具體的比對過程
public boolean doesTree1haveTree2(TreeNode root1,TreeNode root2) {
if(root2 == null)
return true;
if(root1 == null)
return false;
if(root1.val != root2.val){
return false;
}
//如果根節點可以對應上,那麼就去分別比對左子樹和右子樹是否對應上
return doesTree1haveTree2(root1.left, root2.left) && doesTree1haveTree2(root1.right, root2.right);
}
}-
7.二叉樹的映象
操作給定的二叉樹,將其變換為源二叉樹的映象。
二叉樹的映象定義:源二叉樹
8
/ \
6 10
/ \ / \
5 7 9 11
映象二叉樹
8
/ \
10 6
/ \ / \
11 9 7 5/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
import java.util.Stack;
public class Solution {
/**
* 演算法步驟
* 1.節點為空直接返回
* 2.如果這個節點的左右子樹不為空,就交換。
* 3.遞迴對這個節點的左子樹進行求映象。對這個節點的右子樹求映象。
* @param root
*/
public void Mirror(TreeNode root){
if (root == null) {
return;
}
if(root.left != null || root.right != null) {
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
Mirror(root.left);
Mirror(root.right);
}
}
/*public void Mirror(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<TreeNode>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
if (node.left != null || node.right != null) {
TreeNode temp = node.left;
node.left = node.right;
node.right = temp;
}
if(node.left != null)
stack.push(node.left);
if(node.right != null)
stack.push(node.right);
}
}*/
}8、二叉搜素樹的後序遍歷序列
輸入一個整數陣列,判斷該陣列是不是某二叉搜尋樹的後序遍歷的結果。如果是則輸出Yes,否則輸出No。假設輸入的陣列的任意兩個數字都互不相同。
public class Solution {
/**二叉搜尋樹的性質:
* 所有左子樹的節點小於根節點,所有右子樹的節點值大於根節點的值。
* 演算法步驟:
* 1.後序遍歷的最後一個值為root,在前面的陣列中找到第一個大於root值的位置。
* 2.這個位置的前面是root的左子樹,右邊是右子樹。然後左右子樹分別進行這個遞迴操作。
* 3.其中,如果右邊子樹中有比root值小的直接返回false
* @param sequence
* @return
*/
public boolean VerifySquenceOfBST(int [] sequence) {
if (sequence == null || sequence.length == 0)
return false;
return IsBST(sequence, 0, sequence.length -1);
}
public boolean IsBST(int [] sequence, int start, int end) {
if(start >= end) //注意這個條件的新增// 如果對應要處理的資料只有一個或者已經沒
//有資料要處理(start>end)就返回true
return true;
int index = start;
for (; index < end; index++) {//尋找大於root的第一個節點,然後再分左右兩部分
if(sequence[index] > sequence[end])
break;
}
for (int i = index; i < end; i++) {//若右子樹有小於根節點的值,直接返回false
if (sequence[i] < sequence[end]) {
return false;
}
}
return IsBST(sequence, start, index-1) && IsBST(sequence, index, end-1);
}
}/*當案例為{4,6,7,5}的時候就可以看到:
(此時start為0,end為3)
一開始index處的值為1,左邊4的是start為0,index-1為0,下一次遞迴的start和end是一樣的,true!
右邊,start為1,end-1為2,是{6,7}元素,下一輪遞迴是:
————7為root,index的值指向7,
————所以左邊為6,start和index-1都指向6,返回true。
————右邊index指向7,end-1指向6,這時候end > start!如果這部分還不返回true,下面的陣列肯定超了 */
9、二叉搜尋樹與雙向連結串列
題目描述
輸入一棵二叉搜尋樹,將該二叉搜尋樹轉換成一個排序的雙向連結串列。要求不能建立任何新的結點,只能調整樹中結點指標的指向。
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
/**二叉搜尋樹的中序遍歷就是遞增的排序,所以就運用中序遍歷方法來做。
* 演算法思想:
* 中序遍歷的步驟,只不過在遞迴的中間部分不是輸出節點值,而是調整指標指向。
* 10
* /\
* 5 12
* /\
* 4 7
* 步驟記住就行,第一次執行,到4的時候,head和resulthead都指向這個
* 指標調整的其中一步:4是head 5是pRootOfTree 然後調整head右指向5,5左指向4,然後5變成head就行了。
* @param pRootOfTree
* @return
*/
TreeNode head = null;
TreeNode resultHead = null; //儲存生成連結串列的頭結點,便於程式返回
public TreeNode Convert(TreeNode pRootOfTree) {
ConvertSub(pRootOfTree);
return resultHead;
}
public void ConvertSub(TreeNode pRootOfTree) {
if(pRootOfTree == null)
return;
ConvertSub(pRootOfTree.left);
if(head == null){
head = pRootOfTree;
resultHead = pRootOfTree;
}
else {
head.right = pRootOfTree;
pRootOfTree.left = head;
head = pRootOfTree;
}
ConvertSub(pRootOfTree.right);
}
}10、二叉樹的深度
題目描述
輸入一棵二叉樹,求該樹的深度。從根結點到葉結點依次經過的結點(含根、葉結點)形成樹的一條路徑,最長路徑的長度為樹的深度。
/**
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
// 注意最後加1,因為左右子樹的深度大的+根節點的深度1
public int TreeDepth(TreeNode root) {
if(root == null)
return 0;
int left = TreeDepth(root.left);
int right = TreeDepth(root.right);
return left > right? left +1:right+1;
}
}11、平衡二叉樹
輸入一棵二叉樹,判斷該二叉樹是否是平衡二叉樹
描述:如果某二叉樹中任意節點的左右子樹的深度相差不超過1,那麼它就是一棵平衡二叉樹。
public class Solution {
// 注意使用全域性變數
boolean isBalance = true;
public boolean IsBalanced_Solution(TreeNode root) {
lengthOfTree(root);
return isBalance;
}
private int lengthOfTree(TreeNode root) {
if (root == null)
return 0;
int left = lengthOfTree(root.left);
int right = lengthOfTree(root.right);
if (Math.abs(left - right) > 1)
isBalance = false;
return Math.max(left, right) + 1;
}
}第二種Better思路:從底向上判斷,這樣可以記錄下一層的深度
public class Solution {
public boolean IsBalanced(TreeNode root) {
int depth = 0;
return IsBalanced(root, depth);
}
public boolean IsBalanced(TreeNode root, int depth) {
if (root == null) {
depth = 0;
return true;
}
int left = 0, right = 0;
if (IsBalanced(root.left, left) && IsBalanced(root.right, right)) {
int diff = left - right;
if (diff <= 1 && diff >= -1) {
depth = 1 + (left > right ? left : right);
return true;
}
}
return false;
}
}12、二叉樹的下一個節點
題目描述
給定一個二叉樹和其中的一個結點,請找出中序遍歷順序的下一個結點並且返回。注意,樹中的結點不僅包含左右子結點,同時包含指向父結點的指標。
/*
public class TreeLinkNode {
int val;
TreeLinkNode left = null;
TreeLinkNode right = null;
TreeLinkNode next = null;
TreeLinkNode(int val) {
this.val = val;
}
}
*/
public class Solution {
/**參考左程雲和有詳解部落格的思路,
* 主要分三種:
* 1.如果有右孩子,後繼節點就是最左邊的
* 2.如果沒有右孩子,判斷是否是父節點的左孩子,是的話,返回,不是繼續網上找
* 3.找不到就是null
* @param pNode
* @return
*/
public TreeLinkNode GetNext(TreeLinkNode pNode)
{
if(pNode == null)
return null;
// 如果有右子樹,則找右子樹的最左節點
if (pNode.right != null) {
pNode = pNode.right;
// 如果此時pNode沒有左子樹,那麼它就是下一個結點 ,就是最左邊的了
//如果有左子樹,那就在左子樹找最左邊的
while(pNode.left != null)
pNode = pNode.left;
return pNode;
}
//// 非跟結點,並且沒有右子樹
while(pNode.next != null) {
// 找到一個結點是該其父親的左孩子 ,找到就是返回父節點作為後記
if (pNode.next.left == pNode)
return pNode.next;
//找不到這個左孩子的,就繼續往上,next其實是parent
pNode = pNode.next;
}
return null;
}
}13、對稱的二叉樹
請實現一個函式,用來判斷一顆二叉樹是不是對稱的。注意,如果一個二叉樹同此二叉樹的映象是同樣的,定義其為對稱的。
/*
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
public class Solution {
//利用遞迴進行判斷,
//若左子樹的左孩子等於右子樹的右孩子且左子樹的右孩子等於右子樹的左孩子,
//並且左右子樹節點的值相等,則是對稱的。
boolean isSymmetrical(TreeNode pRoot)
{
if (pRoot == null)
return true;
return isCommon(pRoot.left,pRoot.right);
}
public boolean isCommon(TreeNode leftNode, TreeNode rightNode) {
if (leftNode == null && rightNode == null)
return true;
if (leftNode != null && rightNode != null) {
return leftNode.val == rightNode.val &&
isCommon(leftNode.left, rightNode.right) &&
isCommon(leftNode.right, rightNode.left);
}
return false;
}
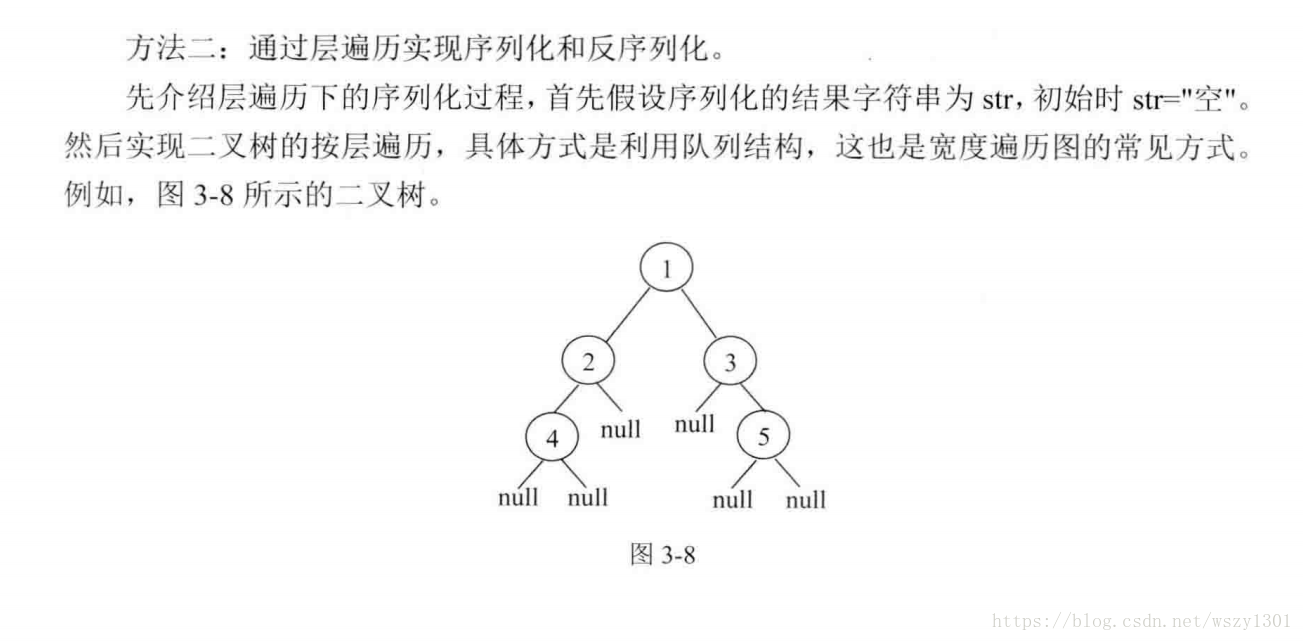
}14、序列化二叉樹
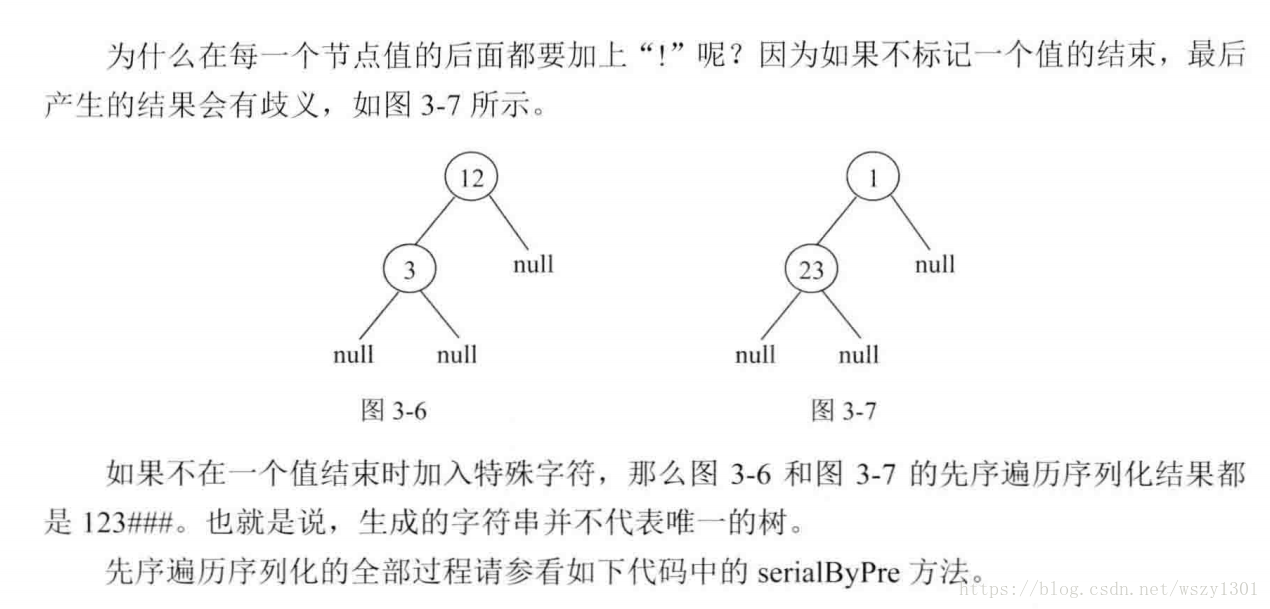
請實現兩個函式,分別用來序列化和反序列化二叉樹
這段程式碼是按照先序遍歷的方法來做的:
/*
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
}
*/
import java.util.LinkedList;
import java.util.Queue;
public class Solution {
//主要運用左程雲的程式設計思想的方式來實現
String Serialize(TreeNode root) {
if(root == null)
return "#!";
String res = root.val+"!";
res = res + Serialize(root.left);
res = res + Serialize(root.right);
return res;
}
TreeNode Deserialize(String str) {
String [] values = str.split("!");
Queue<String> queue = new LinkedList<String>();
for (int i = 0; i < values.length; i++) {
queue.offer(values[i]);
}
return reconPre(queue);
}
TreeNode reconPre(Queue<String> queue) {
String value = queue.poll();
if(value.equals("#"))
return null;
TreeNode head = new TreeNode(Integer.valueOf(value));
head.left = reconPre(queue);
head.right = reconPre(queue);
return head;
}
}三、字串
-
1.正則表示式的匹配
請實現一個函式用來匹配包括'.'和'*'的正則表示式。模式中的字元'.'表示任意一個字元,而'*'表示它前面的字元可以出現任意次(包含0次)。 在本題中,匹配是指字串的所有字元匹配整個模式。例如,字串"aaa"與模式"a.a"和"ab*ac*a"匹配,但是與"aa.a"和"ab*a"均不匹配。
思路:參考網上的思路,主要就是分程式中的兩種情況來討論。第二位是不是*
/*
當模式中的第二個字元不是“*”時:
1、如果字串第一個字元和模式中的第一個字元相匹配,
那麼字串和模式都後移一個字元,然後匹配剩餘的。
2、如果字串第一個字元和模式中的第一個字元相不匹配,直接返回false。
而當模式中的第二個字元是“*”時:
如果字串第一個字元跟模式第一個字元不匹配,則模式後移2個字元,繼續匹配。
如果字串第一個字元跟模式第一個字元匹配,可以有3種匹配方式:
1、模式後移2字元,相當於x*被忽略;
2、字串後移1字元,模式後移2字元; 相當於x*算一次
3、字串後移1字元,模式不變,即繼續匹配字元下一位,因為*可以匹配多位,相當於算多次
這裡需要注意的是:Java裡,要時刻檢驗陣列是否越界。*/
public class Zhengze {
public boolean match(char[] str, char[] pattern) {
if (str == null || pattern == null) {
return false;
}
int strIndex = 0;
int patternIndex = 0;
return matchCore(str, strIndex, pattern, patternIndex);
}
public boolean matchCore(char[] str, int strIndex, char[] pattern, int patternIndex) {
// 有效性檢驗:str到尾,pattern到尾,匹配成功
if (strIndex == str.length && patternIndex == pattern.length)
return true;
// pattern先到尾,匹配失敗
if (strIndex != str.length && patternIndex == pattern.length)
return false;
// 模式第2個是*,且字串第1個跟模式第1個匹配,分3種匹配模式;如不匹配,模式後移2位
if (patternIndex + 1 < pattern.length && pattern[patternIndex + 1] == '*') {
if ((strIndex != str.length && pattern[patternIndex] == str[strIndex])
|| (pattern[patternIndex] == '.' && strIndex != str.length)) {
return // 模式後移2,視為x*匹配0個字元
matchCore(str, strIndex, pattern, patternIndex + 2)
// 視為模式匹配1個字元
|| matchCore(str, strIndex + 1, pattern, patternIndex + 2)
// *匹配1個,再匹配str中的下一個
|| matchCore(str, strIndex + 1, pattern, patternIndex);
} else {
return matchCore(str, strIndex, pattern, patternIndex + 2);
}
} // 模式第2個不是*,且字串第1個跟模式第1個匹配,則都後移1位,否則直接返回false
if ((strIndex != str.length && pattern[patternIndex] == str[strIndex])
|| (pattern[patternIndex] == '.' && strIndex != str.length)) {
return matchCore(str, strIndex + 1, pattern, patternIndex + 1);
}
return false;
}
}
-
2.表示數值的字串
請實現一個函式用來判斷字串是否表示數值(包括整數和小數)。例如,字串"+100","5e2","-123","3.1416"和"-1E-16"都表示數值。 但是"12e","1a3.14","1.2.3","+-5"和"12e+4.3"都不是。
思路:按照一定的規則,如果第一位是+或-,就後移一位。
如果是數字,索引後移,數字表示1.
如果是點,要判斷至此點的數量和e的數量是否已經有了,因為java 中e要求後面為整數,如果有了肯定false。索引後移,dotnum增加。
如果是e,判斷是否重複e,或者前面沒有數字返回false。enum++, 索引++,此時還要判斷最後一位是不是e或者+或者-,如果是false。
public class StrexpressNum {
/*例子:
* 110 1a1 1.1.1 2.2 12e
*
* */
public static boolean isNumeric(char[] str) {
if(str == null)
return false;
int length = str.length;
int dotNum = 0;//記錄點的數量
int index = 0;//索引
int eNum = 0;//記錄e的數量
int num = 0;//記錄數字的數量
if (str[0] == '+' || str[0] == '-') {
index++;
}
while (index < length) {
if(str[index]>='0' && str[index]<='9') {
index++;
num = 1;
// .前面可以沒有數字,所以不需要判斷num是否為0
}else if(str[index]=='.') {
// e後面不能有.,e的個數不能大於1.java科學計數要求aeb,b為整數
if(dotNum >0 || eNum >0)
return false;
dotNum++;
index++;
}else if(str[index] == 'e' || str[index] == 'E') {
// 重複e或者e前面沒有數字
if(eNum > 0 || num ==0)
return false;
eNum++;
index++;
// 符號不能在最後一位
if(index < length &&(str[index]=='+'||str[index]=='-'))
index++;
// 表示e或者符號在最後一位
if(index == length)
return false;
}else {
return false;
}
}
return true;
}
public static void main(String[] args) {
char [] str = {'1','2','e'};
System.out.println(isNumeric(str));
}
}或者用正則表示式來匹配:
[+-]? 表示+或者-出現0次或1次。[0-9]{0,}表示0到9出現0次或者更多次。()表示這個分組作為一個整體。 \\.?表示.出現0次或1次。[0-9]{1,}表示0到9出現1次或者多次。()表示一個分組。如果把兩個分組去掉進行判斷是不準確的。100匹配到[0-9]{1,}出錯。
public boolean isNumeric(char[] str) {
String res = String.valueOf(str);
return res.matches("[+-]?[0-9]{0,}(\\.?[0-9]{1,})?([Ee][+-]?[0-9]{1,})?");
}-
3.0第一個只出現一次的字元
題目描述
在一個字串(0<=字串長度<=10000,全部由字母組成)中找到第一個只出現一次的字元,並返回它的位置, 如果沒有則返回 -1(需要區分大小寫).
import java.util.LinkedHashMap;
public class Solution {
public int FirstNotRepeatingChar(String str) {
//這個hashmap有序,所以用這個
LinkedHashMap<Character, Integer> map= new LinkedHashMap<>();
//遍歷字串,第一次設為1 否則就加
for (int i = 0; i < str.length(); i++) {
if (!map.containsKey(str.charAt(i))) {
map.put(str.charAt(i), 1);
}
else
map.put(str.charAt(i),map.get(str.charAt(i))+1);
}
//找出現次數為1的
for (int i = 0; i < str.length(); i++) {
if (map.get(str.charAt(i)) == 1) {
return i;
}
}
return -1;
}
}-
3.1字元流中第一個不重複的字元
請實現一個函式用來找出字元流中第一個只出現一次的字元。例如,當從字元流中只讀出前兩個字元"go"時,第一個只出現一次的字元是"g"。當從該字元流中讀出前六個字元“google"時,第一個只出現一次的字元是"l"。如果當前字元流沒有存在出現一次的字元,返回#字元
思路:參考兩個部落格一種用hashmap來做,一種用字元陣列來做。
hashmap方法:
HashMap<Character, Integer> map = new HashMap<>();//記錄字元出現次數
ArrayList<Character> list = new ArrayList<>();//記錄當前的所有的字元
//Insert one char from stringstream
public void Insert(char ch)
{
if(map.containsKey(ch))
map.put(ch, map.get(ch)+1);
else
map.put(ch,1);
list.add(ch);
}
//return the first appearence once char in current stringstream
public char FirstAppearingOnce()
{
for(char c:list) {
if(map.get(c)==1)
return c;
}
return '#';
}字元陣列的方法:
char型別和int型別數值在 0-255之內的可以通用
預設初始值是ASCII的0(int);char型別會自動轉換成(int型)ASCII進行算術運算
char [] chars = new char[256];//ascii字元共128,其他字元非中文認為256個,
//為每個字元預留空間。預設每個存的ascii值為0
StringBuffer sb = new StringBuffer();//記錄當前的所有字元
//Insert one char from stringstream
public void Insert(char ch)
{
sb.append(ch);
chars[ch]++;//如果字元是1,那麼就是在字元1對應的下標的地方
//也就是49的下標處,ascii加1.此時如果輸出chars[ch],裡面存ascii值
//為1,所以是一個不可顯示的字元。
}
//return the first appearence once char in current stringstream
public char FirstAppearingOnce()
{
char [] str = sb.toString().toCharArray();
for(char c:str) {
if(chars[c] == 1)//判斷這個字元陣列中在這個字元下標處值是否為1.
return c;
}
return '#';
}-
4.翻轉字串
牛客最近來了一個新員工Fish,每天早晨總是會拿著一本英文雜誌,寫些句子在本子上。同事Cat對Fish寫的內容頗感興趣,有一天他向Fish借來翻看,但卻讀不懂它的意思。例如,“student. a am I”。後來才意識到,這傢伙原來把句子單詞的順序翻轉了,正確的句子應該是“I am a student.”。Cat對一一的翻轉這些單詞順序可不在行,你能幫助他麼?
思路:兩個思路,一個比較簡單的就是用空格切分出來,student. a am I。然後從後往前新增到stringbuffer裡面。
另一個思路就是基本思路劍指offer,先將整個字串翻轉,然後將每個單詞翻轉。i love you 反轉就是 uoy evol i,然後再每個單詞進行反轉。
public class Fanzhuan {
//第一種方法,用空格將字串切分,
//倒著往stringbuffer裡面插入。
public String ReverseSentence1(String str) {
if (str == null || str.trim().length() == 0) {
return str;
}
String[] strs =str.split(" ");//str = "i love you"則strs[0]=i strs[1]=love
StringBuffer sb = new StringBuffer();
for (int i = strs.length -1; i >= 0; i--) {
sb.append(strs[i]);
if (i>0) {//最後一個不新增空格
sb.append(" ");
}
}
return sb.toString();
}
//第二種思路,先將整個字串反轉,再逐個單詞反轉
public String ReverseSentence(String str) {
if (str == null || str.length() == 0)
return str;
if (str.trim().length() == 0)
return str;
StringBuilder sb = new StringBuilder();
String re = reverse(str);
String[] s = re.split(" ");
for (int i = 0; i < s.length - 1; i++) {
sb.append(reverse(s[i]) + " ");
}
sb.append(reverse(s[s.length-1]));
return String.valueOf(sb);
}
public String reverse(String str) {
StringBuilder sb = new StringBuilder();
for (int i = str.length() - 1; i >= 0 ; i--) {
sb.append(str.charAt(i));
}
return String.valueOf(sb);
}
}
-
5.左旋轉字串
組合語言中有一種移位指令叫做迴圈左移(ROL),現在有個簡單的任務,就是用字串模擬這個指令的運算結果。對於一個給定的字元序列S,請你把其迴圈左移K位後的序列輸出。例如,字元序列S=”abcXYZdef”,要求輸出迴圈左移3位後的結果,即“XYZdefabc”。是不是很簡單?OK,搞定它!
思路:前n位反轉,後幾位反轉,最後總的反轉
先反轉前n位,再反轉後幾位,變為了cbafedZYX,再整體反轉變為XYZdefabc
public String LeftRotateString(String str,int n) {
if (str == null || str.trim().length() == 0) {
return str;
}
int len = str.length();
n = n % len;// 當len=3,n=4,其實相當於左旋轉1位,所以需要取餘
char[] charstr = str.toCharArray();
//先旋轉前面的
reverse(charstr, 0, n-1);
//再旋轉後面的字串
reverse(charstr, n, len -1);
//最後整體反轉
reverse(charstr, 0, len-1);
return String.valueOf(charstr);
}
//實現的是charstrs從i到j的反轉,也可以使用上題中stringbuffer的反轉方式
private void reverse(char[] charStrs, int i, int j) {
while(i<j) {
char temp = charStrs[i];
charStrs[i] =charStrs[j];
charStrs[j] = temp;
i++;
j--;
}
}
-
5.把字串轉換為整數
將一個字串轉換成一個整數,要求不能使用字串轉換整數的庫函式。 數值為0或者字串不是一個合法的數值則返回0
思路:若為負數,則輸出負數,字元0對應48,9對應57,不在範圍內則返回false。
public class Strtoint {
public int StrToInt(String str) {
if (str == null || str.length() == 0)
return 0;
int mark = 0;
int number = 0;
char[] chars = str.toCharArray();
if (chars[0] == '-')
mark = 1;//第一位如果是-號,則從第二位開始迴圈
for (int i = mark; i < chars.length; i++) {
if(chars[i] == '+')
continue;
if(chars[i]<48 || chars[i]>57)
return 0;
number = number * 10+chars[i] - 48;
}
return mark==0?number:-number;//最後根據mark標記的正負號來決定數字正負
}
}
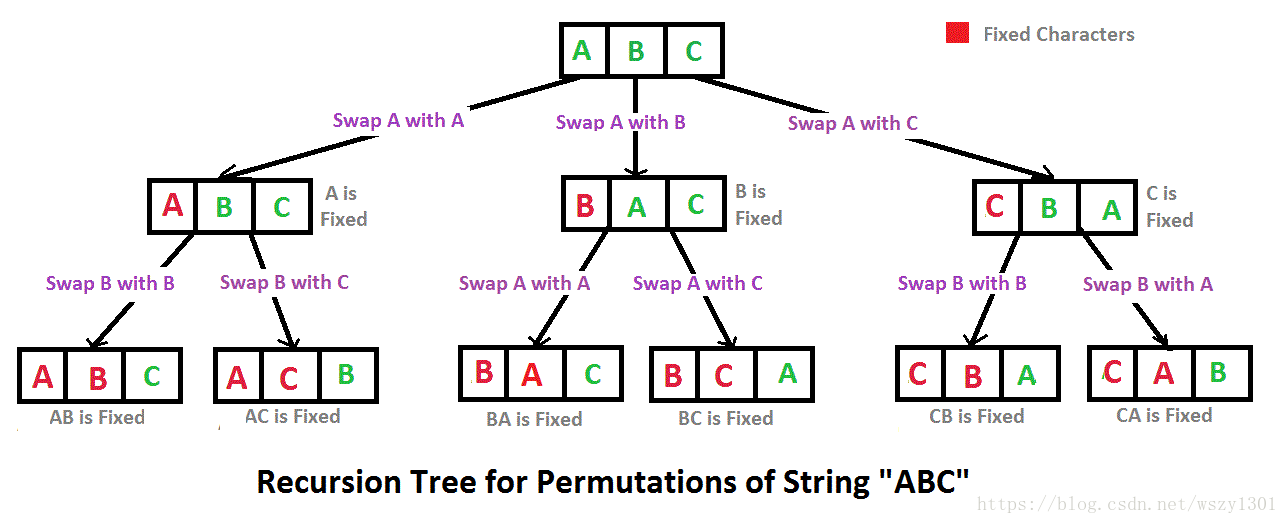
6、字串的排列
題目描述
輸入一個字串,按字典序打印出該字串中字元的所有排列。例如輸入字串abc,則打印出由字元a,b,c所能排列出來的所有字串abc,acb,bac,bca,cab和cba。
輸入描述:
輸入一個字串,長度不超過9(可能有字元重複),字元只包括大小寫字母import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class Solution {
//解法來源:牛客網評論。基於回溯的遞迴實現。
/**劍指offer的思路解析。
* 步驟:
*
* @param str
* @return
*/
public ArrayList<String> Permutation(String str) {
List <String> res = new ArrayList<String>();
if(str != null && str.length() >0){
PermutationHelp(str.toCharArray(),0,res);
Collections.sort(res); //按字典序 輸出字串陣列。
}
return (ArrayList)res;
}
public void PermutationHelp(char[] chars, int index, List<String> list) {
if(index == chars.length -1){ //當遞迴交換到最後一個位置的時候,就看看list有麼有這個字串,沒有的話就放進去。
String val = String.valueOf(chars);
if (!list.contains(val)) {//如果最後list沒有這個string,因為可能交換後有重複的
list.add(val);
}
}
else {
for (int i = index; i < chars.length; i++) { //迴圈來執行交換操作,先交換,然後固定這個,下一個交換。最後要交換回來不要影響執行
swap(chars, index, i);
PermutationHelp(chars, index+1, list);//依次固定一個
swap(chars, index, i);
}
}
}
public void swap(char[] chars,int i, int j) {//交換陣列中的兩個位置中的值
char temp =chars[i];
chars[i] = chars[j];
chars[j] = temp;
}
}四、陣列
-
1.陣列中重複的數字
在一個長度為n的數組裡的所有數字都在0到n-1的範圍內。 陣列中某些數字是重複的,但不知道有幾個數字是重複的。也不知道每個數字重複幾次。請找出陣列中任意一個重複的數字。 例如,如果輸入長度為7的陣列{2,3,1,0,2,5,3},那麼對應的輸出是第一個重複的數字2
思路:比較好的思路的分析為,陣列中的數字為0到n-1的範圍內。如果這個陣列中沒有重複的數字,則對應的i位置的資料也為i。可以重排此陣列,
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.Set;
public class chongfushuzi {
// 使用排序的方式
public boolean duplicate(int numbers[],int length,int [] duplication) {
if(numbers == null || numbers.length ==0) {
duplication[0] = -1;
return false;
}
Arrays.sort(numbers);
for (int i = 0; i < length -1; i++) {//注意這個i的範圍可能越界
if(numbers[i] == numbers[i+1]) {
duplication[0] = numbers[i];
return true;
}
}
return false;
}
//使用額外空間的方法。
public boolean duplicate2(int numbers[],int length,int [] duplication) {
if(numbers == null || numbers.length ==0) {
duplication[0] = -1;
return false;
}
ArrayList<Integer> list = new ArrayList<>();
for (int i = 0; i < length; i++) {
if(list.contains(numbers[i])) {
duplication[0] = numbers[i];
return true;
}
list.add(numbers[i]);
}
return false;
}
//使用額外空間的方法。
public boolean duplicate4(int numbers[],int length,int [] duplication) {
if(length < 2||numbers==null){
return false;
}
Set<Integer> ss = new HashSet<Integer>();
for (int i = 0; i < numbers.length; i++) {
if (ss.contains(numbers[i])) {
duplication[0] = numbers[i];
return true;
} else {
ss.add(numbers[i]);
}
}
return false;
}
//比較好的解決方式,時間複雜度O(n),空間複雜度O(1)
//陣列中的數字為0到n-1的範圍內。
//如果這個陣列中沒有重複的數字,則對應的i位置的資料也為i。可以重排此陣列
public boolean duplicate3(int numbers[],int length,int [] duplication) {
if(numbers == null || numbers.length ==0) {
duplication[0] = -1;
return false;
}
for (int i = 0; i < length; i++) {
if (numbers[i] < 0 || numbers[i] > length - 1) {
duplication[0] = -1;
return false;
}
}
for (int i = 0; i < length; i++) {
while(numbers[i] != i) {
if(numbers[i] == numbers[numbers[i]]) {
duplication[0] = numbers[i];
return true;
}
else {
int tmp = numbers[i];
numbers[i] = numbers[tmp];
numbers[tmp] = tmp;
}
}
}
return false;
}
}
-
2.構建乘積陣列
給定一個數組A[0,1,...,n-1],請構建一個數組B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。
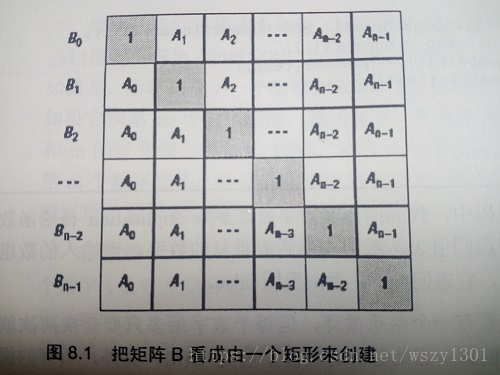
思路:用矩陣的方式,先計算左下三角,再計算右上三角。根據圖來分析即可。
public class MultiArray {
// 新建一個新陣列B, 對A陣列i項左側自上往下累乘,
// 對A陣列i項右側自下往上累乘 時間複雜度O(n)
public int[] multiply(int[] A) {
// 將B拆分為A[0] *...* A[i-1]和A[n-1]*...*A[i+1] 兩部分
if(A == null || A.length ==0)
return A;
int length = A.length;
int [] B = new int[length];
B[0] = 1;
// 先計算左下三角形,此時B[0]只有一個元素,舍為1,
// B[0]不包括A[0]
for (int i = 1; i < length; i++) {
B[i] = B[i-1]*A[i-1];
}
int tmp =1;
//計算右上三角形
for (int i = length -1;