一提到關係型資料庫，我禁不住想：有些東西被忽視了。關係型資料庫無處不在，而且種類繁多，從小巧實用的 SQLite 到強大的 Teradata 。但很少有文章講解資料庫是如何工作的。你可以自己谷歌/百度一下『關係型資料庫原理』，看看結果多麼的稀少【譯者注：百度為您找到相關結果約1,850,000個…】 ，而且找到的那些文章都很短。現在如果你查詢最近時髦的技術（大資料、NoSQL或JavaScript），你能找到更多深入探討它們如何工作的文章。

難道關係型資料庫已經太古老太無趣，除了大學教材、研究文獻和書籍以外，沒人願意講了嗎？

作為一個開發人員，我不喜歡用我不明白的東西。而且，資料庫已經使用了40年之久，一定有理由的。多年以來，我花了成百上千個小時來真正領會這些我每天都在用的、古怪的黑盒子。關係型資料庫

非常有趣，因為它們是基於實用而且可複用的概念。如果你對了解一個數據庫感興趣，但是從未有時間或意願來刻苦鑽研這個內容廣泛的課題，你應該喜歡這篇文章。

雖然本文標題很明確，但我的目的並不是講如何使用資料庫。因此，你應該已經掌握怎麼寫一個簡單的 join query（聯接查詢）和CRUD操作（建立讀取更新刪除），否則你可能無法理解本文。這是唯一需要你瞭解的，其他的由我來講解。

我會從一些電腦科學方面的知識談起，比如時間複雜度。我知道有些人討厭這個概念，但是沒有它你就不能理解資料庫內部的巧妙之處。由於這是個很大的話題，我將集中探討我認為必要的內容：資料庫處理SQL查詢的方式。我僅僅介紹資料庫背後的基本概念，以便在讀完本文後你會對底層到底發生了什麼有個很好的瞭解

。

【譯者注：關於時間複雜度。電腦科學中，演算法的時間複雜度是一個函式，它定量描述了該演算法的執行時間。如果不瞭解這個概念建議先看看維基或百度百科，對於理解文章下面的內容很有幫助】

由於本文是個長篇技術文章，涉及到很多演算法和資料結構知識，你儘可以慢慢讀。有些概念比較難懂，你可以跳過，不影響理解整體內容。

這篇文章大約分為3個部分：

• 底層和上層資料庫元件概況
• 查詢優化過程概況
• 事務和緩衝池管理概況

回到基礎

很久很久以前（在一個遙遠而又遙遠的星系……)，開發者必須確切地知道他們的程式碼需要多少次運算。他們把演算法和資料結構牢記於心，因為他們的計算機執行緩慢，無法承受對CPU和記憶體的浪費。

在這一部分，我將提醒大家一些這類的概念，因為它們對理解資料庫至關重要。我還會介紹資料庫索引的概念。

O(1) vs O(n^2)

現今很多開發者不關心時間複雜度……他們是對的。

但是當你應對大量的資料（我說的可不只是成千上萬哈）或者你要爭取毫秒級操作，那麼理解這個概念就很關鍵了。而且你猜怎麼著，資料庫要同時處理這兩種情景！我不會佔用你太長時間，只要你能明白這一點就夠了。這個概念在下文會幫助我們理解什麼是基於成本的優化。

概念

時間複雜度用來檢驗某個演算法處理一定量的資料要花多長時間。為了描述這個複雜度，電腦科學家使用數學上的『簡明解釋演算法中的大O符號』。這個表示法用一個函式來描述演算法處理給定的資料需要多少次運算。

比如，當我說『這個演算法是適用 O(某函式())』，我的意思是對於某些資料，這個演算法需要 某函式(資料量) 次運算來完成。

重要的不是資料量，而是當資料量增加時運算如何增加。時間複雜度不會給出確切的運算次數，但是給出的是一種理念。

圖中可以看到不同型別的複雜度的演變過程，我用了對數尺來建這個圖。具體點兒說，資料量以很快的速度從1條增長到10億條。我們可得到如下結論：

• 綠：O(1)或者叫常數階複雜度，保持為常數（要不人家就不會叫常數階複雜度了）。
• 紅：O(log(n))對數階複雜度，即使在十億級資料量時也很低。
• 粉：最糟糕的複雜度是 O(n^2)，平方階複雜度，運算數快速膨脹。
• 黑和藍：另外兩種複雜度（的運算數也是）快速增長。

例子

資料量低時，O(1) 和 O(n^2)的區別可以忽略不計。比如，你有個演算法要處理2000條元素。

• O(1) 演算法會消耗 1 次運算
• O(log(n)) 演算法會消耗 7 次運算
• O(n) 演算法會消耗 2000 次運算
• O(n*log(n)) 演算法會消耗 14,000 次運算
• O(n^2) 演算法會消耗 4,000,000 次運算

O(1) 和 O(n^2) 的區別似乎很大（4百萬）,但你最多損失 2 毫秒，只是一眨眼的功夫。確實，當今處理器每秒可處理上億次的運算。這就是為什麼效能和優化在很多IT專案中不是問題。

我說過，面臨海量資料的時候，瞭解這個概念依然很重要。如果這一次演算法需要處理 1,000,000 條元素（這對資料庫來說也不算大）。

• O(1) 演算法會消耗 1 次運算
• O(log(n)) 演算法會消耗 14 次運算
• O(n) 演算法會消耗 1,000,000 次運算
• O(n*log(n)) 演算法會消耗 14,000,000 次運算
• O(n^2) 演算法會消耗 1,000,000,000,000 次運算

我沒有具體算過，但我要說，用O(n^2) 演算法的話你有時間喝杯咖啡（甚至再續一杯！）。如果在資料量後面加個0，那你就可以去睡大覺了。

繼續深入

為了讓你能明白

• 搜尋一個好的雜湊表會得到 O(1) 複雜度
  • 搜尋一個均衡的樹會得到 O(log(n)) 複雜度
  • 搜尋一個陣列會得到 O(n) 複雜度
  • 最好的排序演算法具有 O(n*log(n)) 複雜度
  • 糟糕的排序演算法具有 O(n^2) 複雜度

注：在接下來的部分，我們將會研究這些演算法和資料結構。

有多種型別的時間複雜度

• 一般情況場景
• 最佳情況場景
• 最差情況場景

時間複雜度經常處於最差情況場景。

這裡我只探討時間複雜度，但複雜度還包括：

• 演算法的記憶體消耗
• 演算法的磁碟 I/O 消耗

當然還有比 n^2 更糟糕的複雜度，比如：

• n^4：差勁！我將要提到的一些演算法具備這種複雜度。
• 3^n：更差勁！本文中間部分研究的一些演算法中有一個具備這種複雜度（而且在很多資料庫中還真的使用了）。
• 階乘 n：你永遠得不到結果，即便在少量資料的情況下。
• n^n：如果你發展到這種複雜度了，那你應該問問自己IT是不是你的菜。

注：我並沒有給出『大O表示法』的真正定義，只是利用這個概念。可以看看維基百科上的這篇文章。

合併排序

當你要對一個集合排序時你怎麼做？什麼？呼叫 sort() 函式……好吧，算你對了……但是對於資料庫，你需要理解這個 sort() 函式的工作原理。

優秀的排序演算法有好幾個，我側重於最重要的一種：合併排序。你現在可能還不瞭解資料排序有什麼用，但看完查詢優化部分後你就會知道了。再者，合併排序有助於我們以後理解資料庫常見的聯接操作，即合併聯接 。

合併

與很多有用的演算法類似，合併排序基於這樣一個技巧：將 2 個大小為 N/2 的已排序序列合併為一個 N 元素已排序序列僅需要 N 次操作。這個方法叫做合併。

我們用個簡單的例子來看看這是什麼意思：

通過此圖你可以看到，在 2 個 4元素序列裡你只需要迭代一次，就能構建最終的8元素已排序序列，因為兩個4元素序列已經排好序了：

• 1) 在兩個序列中，比較當前元素（當前=頭一次出現的第一個）
• 2) 然後取出最小的元素放進8元素序列中
• 3) 找到（兩個）序列的下一個元素，(比較後)取出最小的
• 重複1、2、3步驟，直到其中一個序列中的最後一個元素
• 然後取出另一個序列剩餘的元素放入8元素序列中。

這個方法之所以有效，是因為兩個4元素序列都已經排好序，你不需要再『回到』序列中查詢比較。

【譯者注：合併排序詳細原理，其中一個動圖（原圖較長，我做了刪減）清晰的演示了上述合併排序的過程，而原文的敘述似乎沒有這麼清晰，不動戳大。】

如Java工程化、高效能及分散式、高效能、深入淺出。高架構。效能調優、Spring，MyBatis，Netty原始碼分析和大資料等多個知識點。如果你想拿高薪的，想學習的，想就業前景好的，想跟別人競爭能取得優勢的，想進阿里面試但擔心面試不過的，你都可以來，q群號為：856443934

既然我們明白了這個技巧，下面就是我的合併排序虛擬碼。

C

1 2 3 4 5 6 7 8 9 10 11 12 13

array mergeSort(array a)    if(length(a)==1)       return a[0];    end if    //recursive calls    [left_array right_array] := split_into_2_equally_sized_arrays(a);    array new_left_array := mergeSort(left_array);    array new_right_array := mergeSort(right_array);    //merging the 2 small ordered arrays into a big one    array result := merge(new_left_array,new_right_array);    return result;

合併排序是把問題拆分為小問題，通過解決小問題來解決最初的問題（注：這種演算法叫分治法，即『分而治之、各個擊破』）。如果你不懂，不用擔心，我第一次接觸時也不懂。如果能幫助你理解的話，我認為這個演算法是個兩步演算法：

• 拆分階段，將序列分為更小的序列
• 排序階段，把小的序列合在一起（使用合併演算法）來構成更大的序列

拆分階段

在拆分階段過程中，使用3個步驟將序列分為一元序列。步驟數量的值是 log(N) （因為 N=8, log(N)=3）。【譯者注：底數為2，下文有說明】

我怎麼知道這個的？

我是天才！一句話：數學。道理是每一步都把原序列的長度除以2，步驟數就是你能把原序列長度除以2的次數。這正好是對數的定義（在底數為2時）。

排序階段

在排序階段，你從一元序列開始。在每一個步驟中，你應用多次合併操作，成本一共是 N=8 次運算。

• 第一步，4 次合併，每次成本是 2 次運算。
• 第二步，2 次合併，每次成本是 4 次運算。
• 第三步，1 次合併，成本是 8 次運算。

因為有 log(N) 個步驟，整體成本是 N*log(N) 次運算。

【譯者注：這個完整的動圖演示了拆分和排序的全過程，不動戳大。】

合併排序的強大之處

為什麼這個演算法如此強大？

因為：

• 你可以更改演算法，以便於節省記憶體空間，方法是不建立新的序列而是直接修改輸入序列。

• 你可以更改演算法，以便於同時使用磁碟空間和少量記憶體而避免巨量磁碟 I/O。方法是隻向記憶體中載入當前處理的部分。在僅僅100MB的記憶體緩衝區內排序一個幾個GB的表時，這是個很重要的技巧。

• 你可以更改演算法，以便於在 多處理器/多執行緒/多伺服器 上執行。

比如，分散式合併排序是Hadoop（那個著名的大資料框架）的關鍵元件之一。

• 這個演算法可以點石成金（事實如此！）

這個排序演算法在大多數（如果不是全部的話）資料庫中使用，但是它並不是唯一演算法。如果你想多瞭解一些，你可以看看 這篇論文，探討的是資料庫中常用排序演算法的優勢和劣勢。

陣列，樹和雜湊表

既然我們已經瞭解了時間複雜度和排序背後的理念，我必須要向你介紹3種資料結構了。這個很重要，因為它們是現代資料庫的支柱。我還會介紹資料庫索引的概念。

陣列

二維陣列是最簡單的資料結構。一個表可以看作是個陣列，比如：

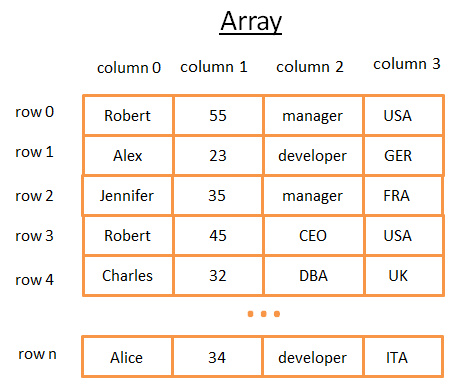
這個二維陣列是帶有行與列的表：

• 每個行代表一個主體
• 列用來描述主體的特徵
• 每個列儲存某一種型別對資料（整數、字串、日期……）

雖然用這個方法儲存和視覺化資料很棒，但是當你要查詢特定的值它就很糟糕了。 舉個例子，如果你要找到所有在 UK 工作的人，你必須檢視每一行以判斷該行是否屬於 UK 。這會造成 N 次運算的成本（N 等於行數），還不賴嘛，但是有沒有更快的方法呢？這時候樹就可以登場了（或開始起作用了）。

樹和資料庫索引

二叉查詢樹是帶有特殊屬性的二叉樹，每個節點的關鍵字必須：

• 比儲存在左子樹的任何鍵值都要大
• 比儲存在右子樹的任何鍵值都要小

【譯者注：binary search tree，二叉查詢樹/二叉搜尋樹，或稱 Binary Sort Tree 二叉排序樹。見百度百科 】

概念

這個樹有 N=15 個元素。比方說我要找208：

• 我從鍵值為 136 的根開始，因為 136<208，我去找節點136的右子樹。
• 398>208，所以我去找節點398的左子樹
• 250>208，所以我去找節點250的左子樹
• 200<208，所以我去找節點200的右子樹。但是 200 沒有右子樹，值不存在（因為如果存在，它會在 200 的右子樹）

現在比方說我要找40

• 我從鍵值為136的根開始，因為 136>40，所以我去找節點136的左子樹。
• 80>40，所以我去找節點 80 的左子樹
• 40=40，節點存在。我抽取出節點內部行的ID（圖中沒有畫）再去表中查詢對應的 ROW ID。
• 知道 ROW ID我就知道了資料在表中對精確位置，就可以立即獲取資料。

最後，兩次查詢的成本就是樹內部的層數。如果你仔細閱讀了合併排序的部分，你就應該明白一共有 log(N)層。所以這個查詢的成本是 log(N)，不錯啊！

回到我們的問題

如Java工程化、高效能及分散式、高效能、深入淺出。高架構。效能調優、Spring，MyBatis，Netty原始碼分析和大資料等多個知識點。如果你想拿高薪的，想學習的，想就業前景好的，想跟別人競爭能取得優勢的，想進阿里面試但擔心面試不過的，你都可以來，q群號為：856443934

上文說的很抽象，我們回來看看我們的問題。這次不用傻傻的數字了，想象一下前表中代表某人的國家的字串。假設你有個樹包含表中的列『country』：

• 如果你想知道誰在 UK 工作
• 你在樹中查詢代表 UK 的節點
• 在『UK 節點』你會找到 UK 員工那些行的位置

這次搜尋只需 log(N) 次運算，而如果你直接使用陣列則需要 N 次運算。你剛剛想象的就是一個資料庫索引。

B+樹索引

查詢一個特定值這個樹挺好用，但是當你需要查詢兩個值之間的多個元素時，就會有大麻煩了。你的成本將是 O(N)，因為你必須查詢樹的每一個節點，以判斷它是否處於那 2 個值之間（例如，對樹使用中序遍歷）。而且這個操作不是磁碟I/O有利的，因為你必須讀取整個樹。我們需要找到高效的範圍查詢方法。為了解決這個問題，現代資料庫使用了一種修訂版的樹，叫做B+樹。在一個B+樹裡：

• 只有最底層的節點（葉子節點）才儲存資訊（相關表的行位置）
• 其它節點只是在搜尋中用來指引到正確節點的。

【譯者注：參考 B+樹 ， 二叉樹遍歷維基百科】

你可以看到，節點更多了（多了兩倍）。確實，你有了額外的節點，它們就是幫助你找到正確節點的『決策節點』（正確節點儲存著相關表中行的位置）。但是搜尋複雜度還是在 O(log(N))（只多了一層）。一個重要的不同點是，最底層的節點是跟後續節點相連線的。

用這個 B+樹，假設你要找40到100間的值：

• 你只需要找 40（若40不存在則找40之後最貼近的值），就像你在上一個樹中所做的那樣。
• 然後用那些連線來收集40的後續節點，直到找到100。

比方說你找到了 M 個後續節點，樹總共有 N 個節點。對指定節點的搜尋成本是 log(N)，跟上一個樹相同。但是當你找到這個節點，你得通過後續節點的連線得到 M 個後續節點，這需要 M 次運算。那麼這次搜尋只消耗了 M+log(N) 次運算，區別於上一個樹所用的 N 次運算。此外，你不需要讀取整個樹（僅需要讀 M+log(N) 個節點）,這意味著更少的磁碟訪問。如果 M 很小（比如 200 行）並且 N 很大（1,000,000），那結果就是天壤之別了。

然而還有新的問題（又來了！）。如果你在資料庫中增加或刪除一行（從而在相關的 B+樹索引裡）：

• 你必須在B+樹中的節點之間保持順序，否則節點會變得一團糟，你無法從中找到想要的節點。
• 你必須儘可能降低B+樹的層數，否則 O(log(N)) 複雜度會變成 O(N)。

換句話說，B+樹需要自我整理和自我平衡。謝天謝地，我們有智慧刪除和插入。但是這樣也帶來了成本：在B+樹中，插入和刪除操作是 O(log(N)) 複雜度。所以有些人聽到過使用太多索引不是個好主意這類說法。沒錯，你減慢了快速插入/更新/刪除表中的一個行的操作，因為資料庫需要以代價高昂的每索引 O(log(N)) 運算來更新表的索引。再者，增加索引意味著給事務管理器帶來更多的工作負荷（在本文結尾我們會探討這個管理器）。

想了解更多細節，你可以看看 Wikipedia 上這篇關於B+樹的文章。如果你想要資料庫中實現B+樹的例子，看看MySQL核心開發人員寫的這篇文章 和 這篇文章。兩篇文章都致力於探討 innoDB(MySQL引擎)如何處理索引。

雜湊表

我們最後一個重要的資料結構是雜湊表。當你想快速查詢值時，雜湊表是非常有用的。而且，理解雜湊表會幫助我們接下來理解一個數據庫常見的聯接操作，叫做『雜湊聯接』。這個資料結構也被資料庫用來儲存一些內部的東西（比如鎖表或者緩衝池，我們在下文會研究這兩個概念）。

雜湊表這種資料結構可以用關鍵字來快速找到一個元素。為了構建一個雜湊表，你需要定義：

• 元素的關鍵字
  • 關鍵字的雜湊函式。關鍵字計算出來的雜湊值給出了元素的位置（叫做雜湊桶）。
  • 關鍵字比較函式。一旦你找到正確的雜湊桶，你必須用比較函式在桶內找到你要的元素。

一個簡單的例子

我們來看一個形象化的例子：

這個雜湊表有10個雜湊桶。因為我懶，我只給出5個桶，但是我知道你很聰明，所以我讓你想象其它的5個桶。我用的雜湊函式是關鍵字對10取模，也就是我只保留元素關鍵字的最後一位，用來查詢它的雜湊桶：

• 如果元素最後一位是 0，則進入雜湊桶0，
• 如果元素最後一位是 1，則進入雜湊桶1，
• 如果元素最後一位是 2，則進入雜湊桶2，
• …我用的比較函式只是判斷兩個整數是否相等。

【譯者注：取模運算】

比方說你要找元素 78：

• 雜湊表計算 78 的雜湊碼，等於 8。
• 查詢雜湊桶 8，找到的第一個元素是 78。
• 返回元素 78。
• 查詢僅耗費了 2 次運算（1次計算雜湊值，另一次在雜湊桶中查詢元素）。

現在，比方說你要找元素 59：

• 雜湊表計算 59 的雜湊碼，等於9。
• 查詢雜湊桶 9，第一個找到的元素是 99。因為 99 不等於 59， 那麼 99 不是正確的元素。
• 用同樣的邏輯，查詢第二個元素(9)，第三個(79)，……，最後一個(29)。
• 元素不存在。
• 搜尋耗費了 7 次運算。

一個好的雜湊函式

你可以看到，根據你查詢的值，成本並不相同。

如果我把雜湊函式改為關鍵字對 1,000,000 取模（就是說取後6位數字），第二次搜尋只消耗一次運算，因為雜湊桶 00059 裡面沒有元素。真正的挑戰是找到好的雜湊函式，讓雜湊桶裡包含非常少的元素。

在我的例子裡，找到一個好的雜湊函式很容易，但這是個簡單的例子。當關鍵字是下列形式時，好的雜湊函式就更難找了：

• 1 個字串（比如一個人的姓）
• 2 個字串（比如一個人的姓和名）
• 2 個字串和一個日期（比如一個人的姓、名和出生年月日）
• …

如果有了好的雜湊函式，在雜湊表裡搜尋的時間複雜度是 O(1)。

陣列 vs 雜湊表

為什麼不用陣列呢？

嗯，你問得好。

• 一個雜湊表可以只裝載一半到記憶體，剩下的雜湊桶可以留在硬碟上。
• 用陣列的話，你需要一個連續記憶體空間。如果你載入一個大表，很難分配足夠的連續記憶體空間。
• 用雜湊表的話，你可以選擇你要的關鍵字（比如，一個人的國家和姓氏）。

想要更詳細的資訊，你可以閱讀我在Java HashMap 上的文章，是關於高效雜湊表實現的。你不需要了解Java就能理解文章裡的概念。

全域性概覽

我們已經瞭解了資料庫內部的基本元件，現在我們需要回來看看資料庫的全貌了。

資料庫是一個易於訪問和修改的資訊集合。不過簡單的一堆檔案也能達到這個效果。事實上，像SQLite這樣最簡單的資料庫也只是一堆檔案而已，但SQLite是精心設計的一堆檔案，因為它允許你：

• 使用事務來確保資料的安全和一致性
• 快速處理百萬條以上的資料

資料庫一般可以用如下圖形來理解：

撰寫這部分之前，我讀過很多書/論文，它們都以自己的方式描述資料庫。所以，我不會特別關注如何組織資料庫或者如何命名各種程序，因為我選擇了自己的方式來描述這些概念以適應本文。區別就是不同的元件，總體思路為：資料庫是由多種互相互動的元件構成的。

核心元件：

如Java工程化、高效能及分散式、高效能、深入淺出。高架構。效能調優、Spring，MyBatis，Netty原始碼分析和大資料等多個知識點。如果你想拿高薪的，想學習的，想就業前景好的，想跟別人競爭能取得優勢的，想進阿里面試但擔心面試不過的，你都可以來，q群號為：856443934

• 程序管理器（process manager）：很多資料庫具備一個需要妥善管理的程序/執行緒池。再者，為了實現納秒級操作，一些現代資料庫使用自己的執行緒而不是作業系統執行緒。
• 網路管理器（network manager）：網路I/O是個大問題，尤其是對於分散式資料庫。所以一些資料庫具備自己的網路管理器。
• 檔案系統管理器（File system manager）：磁碟I/O是資料庫的首要瓶頸。具備一個檔案系統管理器來完美地處理OS檔案系統甚至取代OS檔案系統，是非常重要的。
• 記憶體管理器（memory manager）：為了避免磁碟I/O帶來的效能損失，需要大量的記憶體。但是如果你要處理大容量記憶體你需要高效的記憶體管理器，尤其是你有很多查詢同時使用記憶體的時候。
• 安全管理器（Security Manager）：用於對使用者的驗證和授權。
• 客戶端管理器（Client manager）：用於管理客戶端連線。
• ……

工具：

• 備份管理器（Backup manager）：用於儲存和恢復資料。
• 復原管理器（Recovery manager）：用於崩潰後重啟資料庫到一個一致狀態。
• 監控管理器（Monitor manager）：用於記錄資料庫活動資訊和提供監控資料庫的工具。
• Administration管理器（Administration manager）：用於儲存元資料（比如表的名稱和結構），提供管理資料庫、模式、表空間的工具。【譯者注：好吧，我真的不知道Administration manager該翻譯成什麼，有知道的麻煩告知，不勝感激……】
• ……

查詢管理器：

• 查詢解析器（Query parser）：用於檢查查詢是否合法
• 查詢重寫器（Query rewriter）：用於預優化查詢
• 查詢優化器（Query optimizer）：用於優化查詢
• 查詢執行器（Query executor）：用於編譯和執行查詢

資料管理器：

• 事務管理器（Transaction manager）：用於處理事務
• 快取管理器（Cache manager）：資料被使用之前置於記憶體，或者資料寫入磁碟之前置於記憶體
• 資料訪問管理器（Data access manager）：訪問磁碟中的資料

在本文剩餘部分，我會集中探討資料庫如何通過如下程序管理SQL查詢的：

• 客戶端管理器
• 查詢管理器
• 資料管理器（含復原管理器）

客戶端管理器

客戶端管理器是處理客戶端通訊的。客戶端可以是一個（網站）伺服器或者一個終端使用者或最終應用。客戶端管理器通過一系列知名的API（JDBC, ODBC, OLE-DB …）提供不同的方式來訪問資料庫。

客戶端管理器也提供專有的資料庫訪問API。

當你連線到資料庫時：

• 管理器首先檢查你的驗證資訊（使用者名稱和密碼），然後檢查你是否有訪問資料庫的授權。這些許可權由DBA分配。
• 然後，管理器檢查是否有空閒程序（或執行緒）來處理你對查詢。
• 管理器還會檢查資料庫是否負載很重。
• 管理器可能會等待一會兒來獲取需要的資源。如果等待時間達到超時時間，它會關閉連線並給出一個可讀的錯誤資訊。
• 然後管理器會把你的查詢送給查詢管理器來處理。
• 因為查詢處理程序不是『不全則無』的，一旦它從查詢管理器得到資料，它會把部分結果儲存到一個緩衝區並且開始給你傳送。
• 如果遇到問題，管理器關閉連線，向你傳送可讀的解釋資訊，然後釋放資源。

查詢管理器

這部分是資料庫的威力所在，在這部分裡，一個寫得糟糕的查詢可以轉換成一個快速執行的程式碼，程式碼執行的結果被送到客戶端管理器。這個多步驟操作過程如下：

• 查詢首先被解析並判斷是否合法
• 然後被重寫，去除了無用的操作並且加入預優化部分
• 接著被優化以便提升效能，並被轉換為可執行程式碼和資料訪問計劃。
• 然後計劃被編譯
• 最後，被執行

這裡我不會過多探討最後兩步，因為它們不太重要。

看完這部分後，如果你需要更深入的知識，我建議你閱讀：

• 關於成本優化的初步研究論文(1979)：關係型資料庫系統存取路徑選擇。這個篇文章只有12頁，而且具備計算機一般水平就能理解。
• 非常好、非常深入的 DB2 9.X 如何優化查詢的介紹
• 非常好的PostgreSQL如何優化查詢的介紹。這是一篇最通俗易懂的文件，因為它講的是『我們來看看在這種情況下，PostgreSQL給出了什麼樣的查詢計劃』，而不是『我們來看看PostgreSQL用的什麼演算法』。
• 官方SQLite優化文件。『易於』閱讀，因為SQLite用的是簡單規則。再者，這是唯一真正解釋SQLite如何工作的官方文件。
• 非常好的SQL Server 2005 如何優化查詢的介紹
• Oracle 12c 優化白皮書
• 2篇查詢優化的教程，第一篇 第二篇。教程來自《資料庫系統概念》的作者，很好的讀物，集中討論磁碟I/O，但是要求具有很好的電腦科學水平。
• 另一個原理教程，這篇教程我覺得更易懂，不過它僅關注聯接運算子（join operators）和磁碟I/O。

查詢解析器

每一條SQL語句都要送到解析器來檢查語法，如果你的查詢有錯，解析器將拒絕該查詢。比如，如果你寫成”SLECT …” 而不是 “SELECT …”，那就沒有下文了。

但這還不算完，解析器還會檢查關鍵字是否使用正確的順序，比如 WHERE 寫在 SELECT 之前會被拒絕。

然後，解析器要分析查詢中的表和欄位，使用資料庫元資料來檢查：

• 表是否存在
• 表的欄位是否存在
• 對某型別欄位的 運算 是否 可能（比如，你不能將整數和字串進行比較，你不能對一個整數使用 substring() 函式）

接著，解析器檢查在查詢中你是否有許可權來讀取（或寫入）表。再強調一次：這些許可權由DBA分配。

在解析過程中，SQL 查詢被轉換為內部表示（通常是一個樹）。

如果一切正常，內部表示被送到查詢重寫器。

查詢重寫器

在這一步，我們已經有了查詢的內部表示，重寫器的目標是：

• 預優化查詢
• 避免不必要的運算
• 幫助優化器找到合理的最佳解決方案

重寫器按照一系列已知的規則對查詢執行檢測。如果查詢匹配一種模式的規則，查詢就會按照這條規則來重寫。下面是（可選）規則的非詳盡的列表：

• 檢視合併：如果你在查詢中使用檢視，檢視就會轉換為它的 SQL 程式碼。
• 子查詢扁平化：子查詢是很難優化的，因此重寫器會嘗試移除子查詢

例如：

MySQL

1 2 3 4 5 6

SELECT PERSON.* FROM PERSON WHERE PERSON.person_key IN (SELECT MAILS.person_key FROM MAILS WHERE MAILS.mail LIKE 'christophe%');

會轉換為：

MySQL

1 2 3 4

SELECT PERSON.* FROM PERSON, MAILS WHERE PERSON.person_key = MAILS.person_key and MAILS.mail LIKE 'christophe%';

• 去除不必要的運算子：比如，如果你用了 DISTINCT，而其實你有 UNIQUE 約束（這本身就防止了資料出現重複），那麼 DISTINCT 關鍵字就被去掉了。
• 排除冗餘的聯接：如果相同的 JOIN 條件出現兩次，比如隱藏在檢視中的 JOIN 條件，或者由於傳遞性產生的無用 JOIN，都會被消除。
• 常數計算賦值：如果你的查詢需要計算，那麼在重寫過程中計算會執行一次。比如 WHERE AGE > 10+2 會轉換為 WHERE AGE > 12 ， TODATE(“日期字串”) 會轉換為 datetime 格式的日期值。
• （高階）分割槽裁剪（Partition Pruning）：如果你用了分割槽表，重寫器能夠找到需要使用的分割槽。
• （高階）物化檢視重寫（Materialized view rewrite）：如果你有個物化檢視匹配查詢謂詞的一個子集，重寫器將檢查檢視是否最新並修改查詢，令查詢使用物化檢視而不是原始表。
• （高階）自定義規則：如果你有自定義規則來修改查詢（就像 Oracle policy），重寫器就會執行這些規則。
• （高階）OLAP轉換：分析/加窗 函式，星形聯接，ROLLUP 函式……都會發生轉換（但我不確定這是由重寫器還是優化器來完成，因為兩個程序聯絡很緊，必須看是什麼資料庫）。

【譯者注： 物化檢視  。謂詞，predicate，條件表示式的求值返回真或假的過程】

重寫後的查詢接著送到優化器，這時候好玩的就開始了。

統計

研究資料庫如何優化查詢之前我們需要談談統計，因為沒有統計的資料庫是愚蠢的。除非你明確指示，資料庫是不會分析自己的資料的。沒有分析會導致資料庫做出（非常）糟糕的假設。

但是，資料庫需要什麼型別的資訊呢？

我必須（簡要地）談談資料庫和作業系統如何儲存資料。兩者使用的最小單位叫做頁或塊（預設 4 或 8 KB）。這就是說如果你僅需要 1KB，也會佔用一個頁。要是頁的大小為 8KB，你就浪費了 7KB。

回來繼續講統計！ 當你要求資料庫收集統計資訊，資料庫會計算下列值：

• 表中行和頁的數量
• 表中每個列中的： 唯一值 資料長度（最小，最大，平均） 資料範圍（最小，最大，平均）

• 表的索引資訊

這些統計資訊會幫助優化器估計查詢所需的磁碟 I/O、CPU、和記憶體使用

對每個列的統計非常重要。 比如，如果一個表 PERSON 需要聯接 2 個列： LAST_NAME, FIRST_NAME。 根據統計資訊，資料庫知道FIRST_NAME只有 1,000 個不同的值，LAST_NAME 有 1,000,000 個不同的值。 因此，資料庫就會按照 LAST_NAME, FIRST_NAME 聯接。 因為 LAST_NAME 不大可能重複，多數情況下比較 LAST_NAME 的頭 2 、 3 個字元就夠了，這將大大減少比較的次數。

不過，這些只是基本的統計。你可以讓資料庫做一種高階統計，叫直方圖。直方圖是列值分佈情況的統計資訊。例如：

• 出現最頻繁的值
• 分位數 【譯者注：http://baike.baidu.com/view/1323572.htm】
• …

這些額外的統計會幫助資料庫找到更佳的查詢計劃，尤其是對於等式謂詞（例如： WHERE AGE = 18 ）或範圍謂詞（例如： WHERE AGE > 10 and AGE < 40），因為資料庫可以更好的瞭解這些謂詞相關的數字型別資料行（注：這個概念的技術名稱叫選擇率）。

統計資訊儲存在資料庫元資料內，例如（非分割槽）表的統計資訊位置：

• Oracle： USER / ALL / DBA_TABLES 和 USER / ALL / DBA_TAB_COLUMNS
• DB2： SYSCAT.TABLES 和 SYSCAT.COLUMNS

統計資訊必須及時更新。如果一個表有 1,000,000 行而資料庫認為它只有 500 行，沒有比這更糟糕的了。統計唯一的不利之處是需要時間來計算，這就是為什麼資料庫大多預設情況下不會自動計算統計資訊。資料達到百萬級時統計會變得困難，這時候，你可以選擇僅做基本統計或者在一個數據庫樣本上執行統計。

舉個例子，我參與的一個專案需要處理每表上億條資料的庫，我選擇只統計10%，結果造成了巨大的時間消耗。本例證明這是個糟糕的決定，因為有時候 Oracle 10G 從特定表的特定列中選出的 10% 跟全部 100% 有很大不同（對於擁有一億行資料的表，這種情況極少發生）。這次錯誤的統計導致了一個本應 30 秒完成的查詢最後執行了 8 個小時，查詢這個現象根源的過程簡直是個噩夢。這個例子顯示了統計的重要性。

注：當然了，每個資料庫還有其特定的更高階的統計。如果你想了解更多資訊，讀讀資料庫的文件。話雖然這麼說，我已經盡力理解統計是如何使用的了，而且我找到的最好的官方文件來自PostgreSQL。

查詢優化器

所有的現代資料庫都在用基於成本的優化（即CBO）來優化查詢。道理是針對每個運算設定一個成本，通過應用成本最低廉的一系列運算，來找到最佳的降低查詢成本的方法。

為了理解成本優化器的原理，我覺得最好用個例子來『感受』一下這個任務背後的複雜性。這裡我將給出聯接 2 個表的 3 個方法，我們很快就能看到即便一個簡單的聯接查詢對於優化器來說都是個噩夢。之後，我們會了解真正的優化器是怎麼做的。

對於這些聯接操作，我會專注於它們的時間複雜度，但是，資料庫優化器計算的是它們的 CPU 成本、磁碟 I/O 成本、和記憶體需求。時間複雜度和 CPU 成本的區別是，時間成本是個近似值（給我這樣的懶傢伙準備的）。而 CPU 成本，我這裡包括了所有的運算，比如：加法、條件判斷、乘法、迭代……還有呢：

• 每一個高階程式碼運算都要特定數量的低階 CPU 運算。
• 對於 Intel Core i7、Intel Pentium 4、AMD Opteron…等，（就 CPU 週期而言）CPU 的運算成本是不同的，也就是說它取決於 CPU 的架構。

使用時間複雜度就容易多了（至少對我來說），用它我也能瞭解到 CBO 的概念。由於磁碟 I/O 是個重要的概念，我偶爾也會提到它。請牢記，大多數時候瓶頸在於磁碟 I/O 而不是 CPU 使用。

索引

在研究 B+樹的時候我們談到了索引，要記住一點，索引都是已經排了序的。

僅供參考：還有其他型別的索引，比如點陣圖索引，在 CPU、磁碟I/O、和記憶體方面與B+樹索引的成本並不相同。

另外，很多現代資料庫為了改善執行計劃的成本，可以僅為當前查詢動態地生成臨時索引。

存取路徑

在應用聯接運算子（join operators）之前，你首先需要獲得資料。以下就是獲得資料的方法。

注：由於所有存取路徑的真正問題是磁碟 I/O，我不會過多探討時間複雜度。

全掃描

如果你讀過執行計劃，一定看到過『全掃描』（或只是『掃描』）一詞。簡單的說全掃描就是資料庫完整的讀一個表或索引。就磁碟 I/O 而言，很明顯全表掃描的成本比索引全掃描要高昂。

範圍掃描

其他型別的掃描有索引範圍掃描，比如當你使用謂詞 ” WHERE AGE > 20 AND AGE < 40 ” 的時候它就會發生。

當然，你需要在 AGE 欄位上有索引才能用到索引範圍掃描。

在第一部分我們已經知道，範圍查詢的時間成本大約是 log(N)+M，這裡 N 是索引的資料量，M 是範圍內估測的行數。多虧有了統計我們才能知道 N 和 M 的值（注： M 是謂詞 “ AGE > 20 AND AGE < 40 ” 的選擇率）。另外範圍掃描時，你不需要讀取整個索引，因此在磁碟 I/O 方面沒有全掃描那麼昂貴。

唯一掃描

如果你只需要從索引中取一個值你可以用唯一掃描。

根據 ROW ID 存取

多數情況下，如果資料庫使用索引，它就必須查詢與索引相關的行，這樣就會用到根據 ROW ID 存取的方式。

例如，假如你執行：

MySQL

1	SELECT LASTNAME, FIRSTNAME from PERSON WHERE AGE = 28

如果 person 表的 age 列有索引，優化器會使用索引找到所有年齡為 28 的人，然後它會去表中讀取相關的行，這是因為索引中只有 age 的資訊而你要的是姓和名。

但是，假如你換個做法：

MySQL

1 2	SELECT TYPE_PERSON.CATEGORY from PERSON ,TYPE_PERSON WHERE PERSON.AGE = TYPE_PERSON.AGE

PERSON 表的索引會用來聯接 TYPE_PERSON 表，但是 PERSON 表不會根據行ID 存取，因為你並沒有要求這個表內的資訊。

雖然這個方法在少量存取時表現很好，這個運算的真正問題其實是磁碟 I/O。假如需要大量的根據行ID存取，資料庫也許會選擇全掃描。

其它路徑

我沒有列舉所有的存取路徑，如果你感興趣可以讀一讀 Oracle文件。其它資料庫裡也許叫法不同但背後的概念是一樣的。

聯接運算子

那麼，我們知道如何獲取資料了，那現在就把它們聯接起來！

我要展現的是3個個常用聯接運算子：合併聯接（Merge join），雜湊聯接（Hash Join）和巢狀迴圈聯接（Nested Loop Join）。但是在此之前，我需要引入新詞彙了：內關係和外關係（ inner relation and outer relation）   。 一個關係可以是：

• 一個表
• 一個索引
• 上一個運算的中間結果（比如上一個聯接運算的結果）

當你聯接兩個關係時，聯接演算法對兩個關係的處理是不同的。在本文剩餘部分，我將假定：

• 外關係是左側資料集
• 內關係是右側資料集

比如， A JOIN B 是 A 和 B 的聯接，這裡 A 是外關係，B 是內關係。

多數情況下， A JOIN B 的成本跟 B JOIN A 的成本是不同的。

在這一部分，我還將假定外關係有 N 個元素，內關係有 M 個元素。要記住，真實的優化器通過統計知道 N 和 M 的值。

注：N 和 M 是關係的基數。【譯者注： 基數 】

巢狀迴圈聯接

巢狀迴圈聯接是最簡單的。

道理如下：

• 針對外關係的每一行
• 檢視內關係裡的所有行來尋找匹配的行

下面是虛擬碼：

C

1 2 3 4 5 6 7 8

nested_loop_join(array outer, array inner)   for each row a in outer     for each row b in inner       if (match_join_condition(a,b))         write_result_in_output(a,b)       end if     end for    end for

由於這是個雙迭代，時間複雜度是 O(N*M)。

在磁碟 I/O 方面， 針對 N 行外關係的每一行，內部迴圈需要從內關係讀取 M 行。這個演算法需要從磁碟讀取 N+ N*M 行。但是，如果內關係足夠小，你可以把它讀入記憶體，那麼就只剩下 M + N 次讀取。這樣修改之後，內關係必須是最小的，因為它有更大機會裝入記憶體。

在CPU成本方面沒有什麼區別，但是在磁碟 I/O 方面，最好最好的，是每個關係只讀取一次。

當然，內關係可以由索引代替，對磁碟 I/O 更有利。

由於這個演算法非常簡單，下面這個版本在內關係太大無法裝入記憶體時，對磁碟 I/O 更加有利。道理如下：

• 為了避免逐行讀取兩個關係，
• 你可以成簇讀取，把（兩個關係裡讀到的）兩簇資料行儲存在記憶體裡，
• 比較兩簇資料，保留匹配的，
• 然後從磁碟載入新的資料簇來繼續比較
• 直到載入了所有資料。

可能的演算法如下：

C

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

// improved version to reduce the disk I/O. nested_loop_join_v2(file outer, file inner)   for each bunch ba in outer   // ba is now in memory     for each bunch bb in inner         // bb is now in memory         for each row a in ba           for each row b in bb             if (match_join_condition(a,b))               write_result_in_output(a,b)             end if           end for        end for     end for    end for

使用這個版本，時間複雜度沒有變化，但是磁碟訪問降低了：

• 用前一個版本，演算法需要 N + N*M 次訪問（每次訪問讀取一行）。
• 用新版本，磁碟訪問變為 外關係的資料簇數量 + 外關係的資料簇數量 * 內關係的資料簇數量。
• 增加資料簇的尺寸，可以降低磁碟訪問。

雜湊聯接

雜湊聯接更復雜，不過在很多場合比巢狀迴圈聯接成本低。

雜湊聯接的道理是：

• 1) 讀取內關係的所有元素
• 2) 在記憶體裡建一個雜湊表
• 3) 逐條讀取外關係的所有元素
• 4) （用雜湊表的雜湊函式）計算每個元素的雜湊值，來查詢內關係裡相關的雜湊桶內
• 5) 是否與外關係的元素匹配。

在時間複雜度方面我需要做些假設來簡化問題：

• 內關係被劃分成 X 個雜湊桶
• 雜湊函式幾乎均勻地分佈每個關係內資料的雜湊值，就是說雜湊桶大小一致。
• 外關係的元素與雜湊桶內的所有元素的匹配，成本是雜湊桶內元素的數量。

時間複雜度是 (M/X) * N + 建立雜湊表的成本(M) + 雜湊函式的成本 * N 。 如果雜湊函式建立了足夠小規模的雜湊桶，那麼複雜度就是 O(M+N)。

還有個雜湊聯接的版本，對記憶體有利但是對磁碟 I/O 不夠有利。 這回是這樣的：

• 1) 計算內關係和外關係雙方的雜湊表
• 2) 儲存雜湊表到磁碟
• 3) 然後逐個雜湊桶比較（其中一個讀入記憶體，另一個逐行讀取）。

合併聯接

合併聯接是唯一產生排序的聯接演算法。

注：這個簡化的合併聯接不區分內表或外表；兩個表扮演同樣的角色。但是真實的實現方式是不同的，比如當處理重複值時。

1.（可選）排序聯接運算：兩個輸入源都按照聯接關鍵字排序。

2.合併聯接運算：排序後的輸入源合併到一起。

排序

我們已經談到過合併排序，在這裡合併排序是個很好的演算法（但是並非最好的，如果記憶體足夠用的話，還是雜湊聯接更好）。

然而有時資料集已經排序了，比如：

如Java工程化、高效能及分散式、高效能、深入淺出。高架構。效能調優、Spring，MyBatis，Netty原始碼分析和大資料等多個知識點。如果你想拿高薪的，想學習的，想就業前景好的，想跟別人競爭能取得優勢的，想進阿里面試但擔心面試不過的，你都可以來，q群號為：856443934

• 如果表內部就是有序的，比如聯接條件裡一個索引組織表 【譯者注： index-organized table 】
• 如果關係是聯接條件裡的一個索引
• 如果聯接應用在一個查詢中已經排序的中間結果

合併聯接

這部分與我們研究過的合併排序中的合併運算非常相似。不過這一次呢，我們不是從兩個關係裡挑選所有元素，而是隻挑選相同的元素。道理如下：

• 1) 在兩個關係中，比較當前元素（當前=頭一次出現的第一個）
• 2) 如果相同，就把兩個元素都放入結果，再比較兩個關係裡的下一個元素
• 3) 如果不同，就去帶有最小元素的關係裡找下一個元素（因為下一個元素可能會匹配）
• 4) 重複 1、2、3步驟直到其中一個關係的最後一個元素。

因為兩個關係都是已排序的，你不需要『回頭去找』，所以這個方法是有效的。

該演算法是個簡化版，因為它沒有處理兩個序列中相同資料出現多次的情況（即多重匹配）。真實版本『僅僅』針對本例就更加複雜，所以我才選擇簡化版。

如果兩個關係都已經排序，時間複雜度是 O(N+M)

如果兩個關係需要排序，時間複雜度是對兩個關係排序的成本：O(N*Log(N) + M*Log(M))

對於計算機極客，我給出下面這個可能的演算法來處理多重匹配（注：對於這個演算法我不保證100%正確）：

C

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

mergeJoin(relation a, relation b)   relation output   integer a_key:=0;   integer  b_key:=0;   while (a[a_key]!=null and b[b_key]!=null)      if (a[a_key] < b[b_key])       a_key++;      else if (a[a_key] > b[b_key])       b_key++;      else //Join predicate satisfied       write_result_in_output(a[a_key],b[b_key])       //We need to be careful when we increase the pointers       if (a[a_key+1] != b[b_key])         b_key++;       end if       if (b[b_key+1] != a[a_key])         a_key++;       end if       if (b[b_key+1] == a[a_key] && b[b_key] == a[a_key+1])         b_key++;         a_key++;       end if     end if   end while

哪個演算法最好？

如果有最好的，就沒必要弄那麼多種型別了。這個問題很難，因為很多因素都要考慮，比如：

• 空閒記憶體：沒有足夠的記憶體的話就跟強大的雜湊聯接拜拜吧（至少是完全記憶體中雜湊聯接）。
• 兩個資料集的大小。比如，如果一個大表聯接一個很小的表，那麼巢狀迴圈聯接就比雜湊聯接快，因為後者有建立雜湊的高昂成本；如果兩個表都非常大，那麼巢狀迴圈聯接CPU成本就很高昂。
• 是否有索引：有兩個 B+樹索引的話，聰明的選擇似乎是合併聯接。
• 結果是否需要排序：即使你用到的是未排序的資料集，你也可能想用成本較高的合併聯接（帶排序的），因為最終得到排序的結果後，你可以把它和另一個合併聯接串起來（或者也許因為查詢用 ORDER BY/GROUP BY/DISTINCT 等操作符隱式或顯式地要求一個排序結果）。
• 關係是否已經排序：這時候合併聯接是最好的候選項。
• 聯接的型別：是等值聯接（比如 tableA.col1 = tableB.col2 ）？ 還是內聯接？外聯接？笛卡爾乘積？或者自聯接？有些聯接在特定環境下是無法工作的。
• 資料的分佈：如果聯接條件的資料是傾斜的（比如根據姓氏來聯接人，但是很多人同姓），用雜湊聯接將是個災難，原因是雜湊函式將產生分佈極不均勻的雜湊桶。
• 如果你希望聯接操作使用多執行緒或多程序。

想要更詳細的資訊，可以閱讀DB2, ORACLE 或 SQL Server)的文件。

簡化的例子

我們已經研究了 3 種類型的聯接操作。

現在，比如說我們要聯接 5 個表，來獲得一個人的全部資訊。一個人可以有：

• 多個手機號（MOBILES）
• 多個郵箱（MAILS）
• 多個地址（ADRESSES）
• 多個銀行賬號（BANK_ACCOUNTS）

換句話說，我們需要用下面的查詢快速得到答案：

MySQL

1 2 3 4 5 6

SELECT * from PERSON, MOBILES, MAILS,ADRESSES, BANK_ACCOUNTS WHERE PERSON.PERSON_ID = MOBILES.PERSON_ID AND PERSON.PERSON_ID = MAILS.PERSON_ID AND PERSON.PERSON_ID = ADRESSES.PERSON_ID AND PERSON.PERSON_ID = BANK_ACCOUNTS.PERSON_ID

作為一個查詢優化器，我必須找到處理資料最好的方法。但有 2 個問題：

• 每個聯接使用那種型別？ 我有 3 種可選（雜湊、合併、巢狀），同時可能用到 0, 1 或 2 個索引（不必說還有多種型別的索引）。

• 按什麼順序執行聯接？ 比如，下圖顯示了針對 4 個表僅僅 3 次聯接，可能採用的執行計劃：

那麼下面就是我可能採取的方法：

• 1) 採取粗暴的方式 用資料庫統計，計算每種可能的執行計劃的成本，保留最佳方案。但是，會有很多可能性。對於一個給定順序的聯接操作，每個聯接有三種可能性：雜湊、合併、巢狀，那麼總共就有 3^4 種可能性。確定聯接的順序是個二叉樹的排列問題，會有 (2*4)!/(4+1)! 種可能的順序。對本例這個相當簡化了的問題，我最後會得到 3^4*(2*4)!/(4+1)! 種可能。