時間序列資料預測
ts(data = NA, start = 1, end = numeric(), frequency = 1,
deltat = 1, ts.eps = getOption(“ts.eps”), class = , names = )
start:第一次觀測的時間。單個數字或兩個整數的向量,它們指定一個自然時間單位和進入時間單位的(基於1的)樣本數量
end:最後一次觀測的時間,用與開始相同的方式指定
frequency:每單位時間的觀測次數
deltat:連續觀測之間取樣週期的百分比;例如,月資料為1/12。
ts.eps:時間序列比較公差。如果頻率的絕對差小於ts.eps,則認為頻率相等
data2 <- read.csv("收入資料.csv")
head(data2)
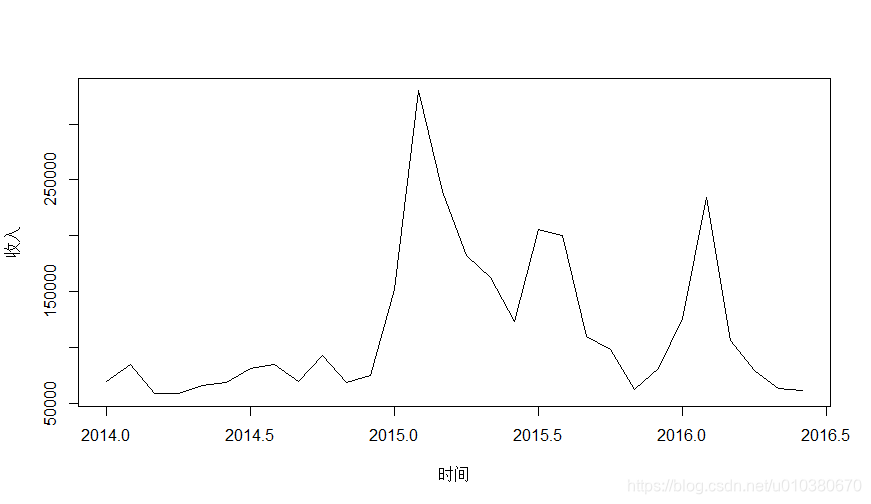
data2.ts <- ts(data2[,2],frequency = 12,start = c(2014,1))
plot(data2.ts,xlab="時間",ylab="收入")
時間序列的平穩性檢驗
unitrootTest(x, lags = 1, type = c(“nc”, “c”, “ct”), title = NULL,
description = NULL)
lags:用於誤差項校正的最大滯後數
type:描述單位根迴歸型別的字串。正確的選項是“nc”表示沒有截距(常數)或時間趨勢的迴歸,“c”表示有截距(常數)但沒有時間趨勢的迴歸,“ct”表示有截距(常數)和時間趨勢的迴歸。預設值是"c"
library(fUnitRoots)
unitrootTest(data2.ts)
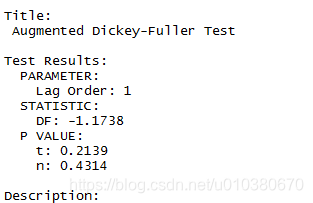
測試返回一個類“fHTEST”的物件,該物件具有以下槽:
@call
the function call.函式呼叫
@data
a data frame with the input data.
@data.name
a character string giving the name of the data frame.
@test
a list object which holds the output of the underlying test function. 底層測試資料的輸出
@title
a character string with the name of the test.
@description
a character string with a brief description of the test.
@test槽的條目包括以下元件:
$statistic
the value of the test statistic.
$parameter
the lag order. 滯後秩序
$p.value
the p-value of the test.
$method
a character string indicating what type of test was performed.指示執行什麼型別的測試
$data.name
a character string giving the name of the data.
$alternative
a character string describing the alternative hypothesis. 描述替代假設
$name
the name of the underlying function, which may be wrapped.
$output
additional test results to be printed.
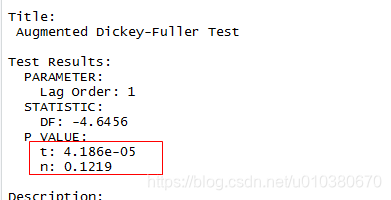
進行差分得到平穩序列
data2.ts.diff <- diff(data2.ts)
unitrootTest(data2.ts.diff)
data2.ts.decompose <- decompose(data2.ts)
plot(data2.ts.decompose)
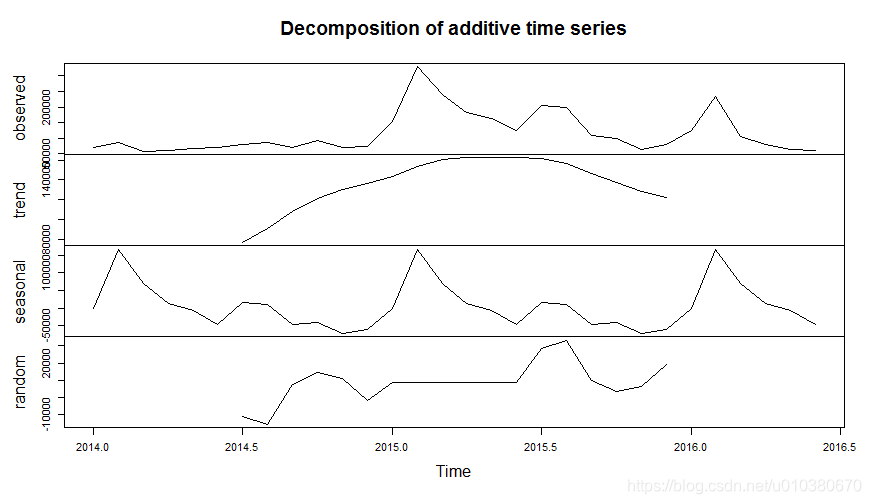
原始序列觀測值、序列分解趨勢圖、序列分解季節變動圖、序列分解噪聲圖
時間序列預測的主要方法:平均(平滑)預測法、長期趨勢預測法、季節變動預測法、指數平滑預測法
指數平滑法是移動平均法中的一種,其特點在於給過去的觀測值不一樣的權重,即較近期觀測值的權數比較遠期觀測值的權數要大。根據平滑次數不同,指數平滑法分為一次指數平滑法、二次指數平滑法和三次指數平滑法等。但它們的基本思想都是:預測值是以前觀測值的加權和,且對不同的資料給予不同的權數,新資料給予較大的權數,舊資料給予較小的權數
HoltWinters(x, alpha = NULL, beta = NULL, gamma = NULL,
seasonal = c(“additive”, “multiplicative”),
start.periods = 2, l.start = NULL, b.start = NULL,
s.start = NULL,
optim.start = c(alpha = 0.3, beta = 0.1, gamma = 0.1),
optim.control = list())
alpha:霍爾特-溫特斯濾波器的引數
beta:霍爾特-溫特斯濾波器的貝塔引數。如果設定為FALSE,函式將進行指數平滑。
gamma:用於季節成分的伽馬引數。如果設定為FALSE,則擬合非季節性模型
seasonal:選擇“加法”(預設)或“乘法”季節性模型的字串。前幾個字元就足夠了。(只在伽馬非零時生效)
HoltWintersModel <- HoltWinters(data2.ts,alpha = TRUE,beta = TRUE,gamma = TRUE)
plot(HoltWintersModel,lty=1,lty.predicted=2)
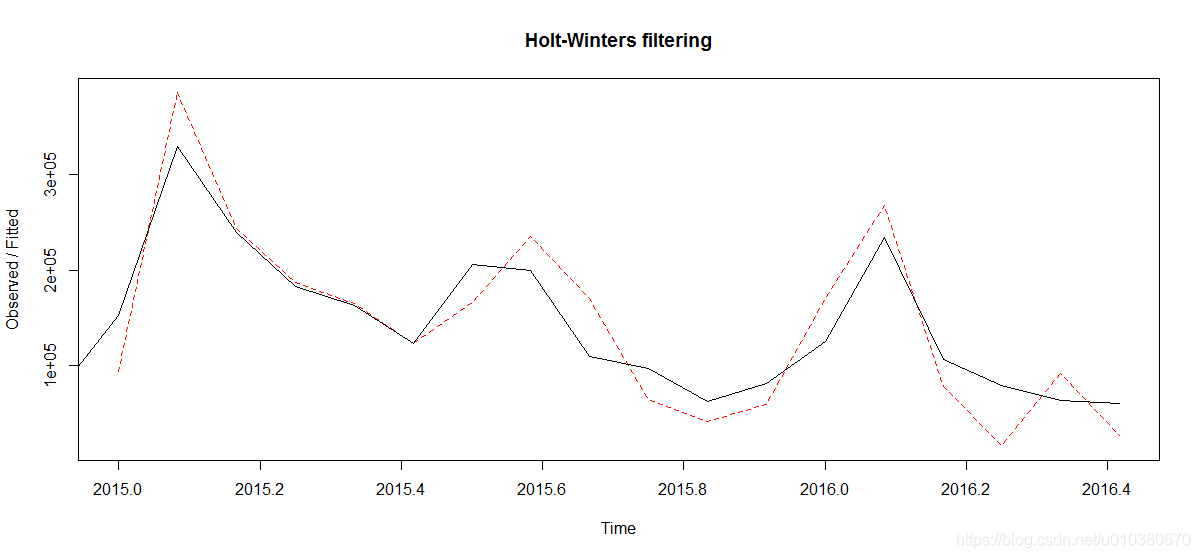
HoltWintersForecast <- forecast(HoltWintersModel,h=6,)
acf(HoltWintersForecast$residuals,lag.max = 20,na.action = na.pass)
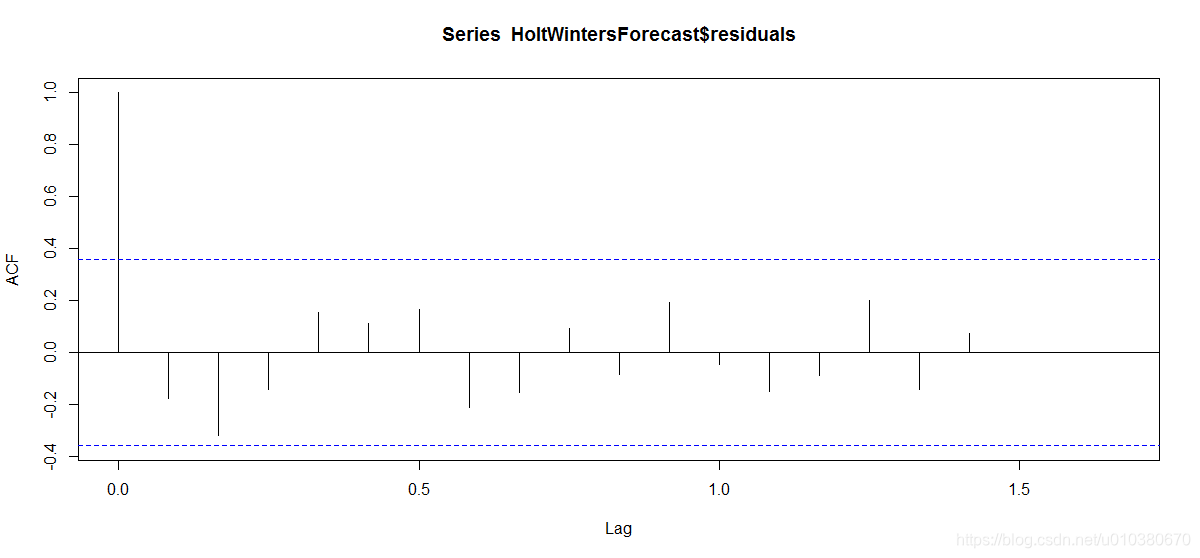
計算acf的最大延遲。預設為10*log10(N/m),其中N為觀測次數,m為級數個數。將自動限制在比本系列觀測值少一次的範圍內。
plot(HoltWintersForecast)
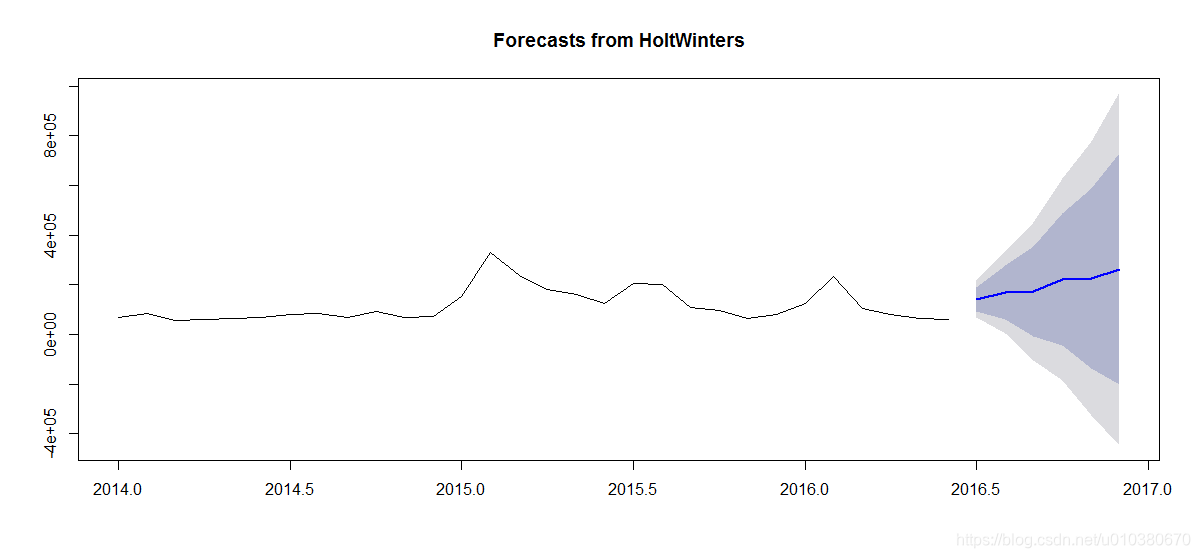
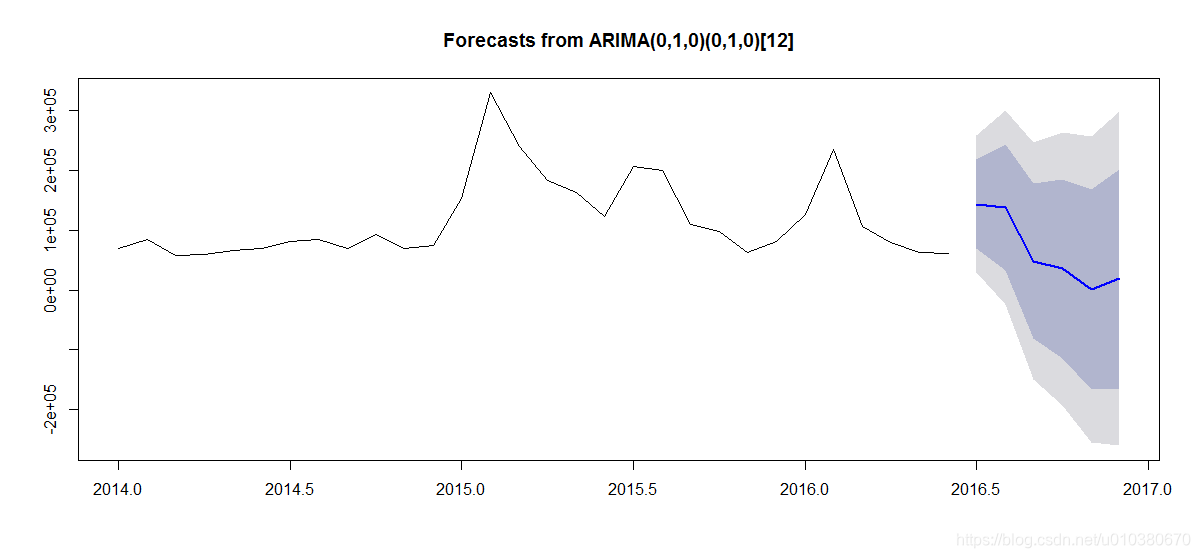
fit <- auto.arima(data2.ts)
fit.forecast <- forecast(fit,h=6)
plot(fit.forecast)