loc 平均值
scale (scale) 標準差
pdf(x, loc=0, scale=1)

正態分佈（Normal distribution），也稱“常態分佈”，又名高斯分佈（Gaussian distribution），最早由A.棣莫弗在求二項分佈的漸近公式中得到。C.F.高斯在研究測量誤差時從另一個角度匯出了它。P.S.拉普拉斯和高斯研究了它的性質。是一個在數學、物理及工程等領域都非常重要的概率分佈，在統計學的許多方面有著重大的影響力。
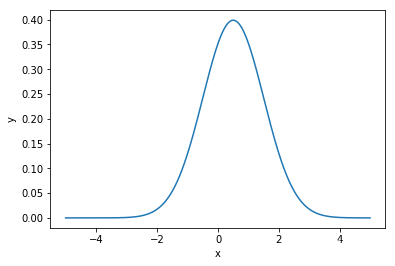
正態曲線呈鍾型，兩頭低，中間高，左右對稱因其曲線呈鐘形，因此人們又經常稱之為鐘形曲線。
若隨機變數X服從一個數學期望為μ、方差為σ^2的正態分佈，記為N(μ，σ^2)。其概率密度函式為正態分佈的期望值μ決定了其位置，其標準差σ決定了分佈的幅度。當μ = 0,σ = 1時的正態分佈是標準正態分佈。

from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
dmean=0.5
dstd=1
x=np.arange(-5,5,0.01)
y=norm.pdf(x,dmean,dstd)
plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.show()