C for Graphic:語言(六)
之前我們依次學習了vertex頂點和fragment片段函式分別能做些什麼事情,這次我們就綜合一下,實現一個帶有vertex頂點和fragment片段函式的完整的CG shader看下效果。
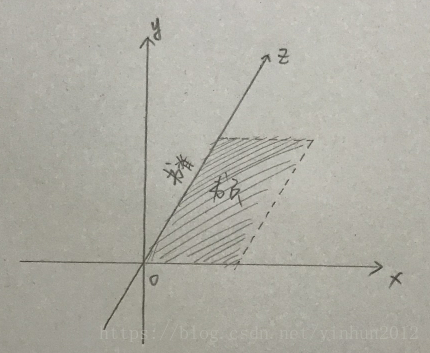
比如我喜歡看書,特別是“物理學”和“心理學”的書,我想通過shader實現簡單的翻書效果,模擬一下真實現實中翻書的動效。首先,我建立一個符合要求的“書頁”了,現實中書本都是以“書脊”為對稱軸開合的,那麼我們就要建立一個以虛擬“書脊”座標系內的“書頁”網格,如下:
因為前面我在圖形輔助工具章節已經講過建立rectangle拓撲網格了,所以這裡我就不再重複講解,程式碼如下:
using System.Collections; using System.Collections.Generic; using UnityEngine; [ExecuteInEditMode] public class YYPlane : MonoBehaviour { public bool Refresh = false; [SerializeField]public int xCount = 100; //單位方塊x軸數量 [SerializeField]public int yCount = 100; //單位方塊y軸數量 private float mCellLen = 0.1f; //單位小方塊邊長 private Mesh mMesh; void Start() { CreateMesh(); } void Update() { if (Refresh) { CreateMesh(); Refresh = false; } } private void CreateMesh() { //構建一個任意單位長寬的長方形 mMesh = new Mesh(); int xPointCount = xCount + 1; //x軸網格點數量 int yPointCount = yCount + 1; //y軸網格點數量 int xyMeshPointCount = xPointCount * yPointCount; //網格頂點的數量 int triangleCount = xCount * yCount * 2; //三角面數量(小正方形的兩倍) //構建mesh網格的所有資訊陣列 Vector3[] vertices = new Vector3[xyMeshPointCount]; int[] triangles = new int[triangleCount * 3]; Vector2[] uvs = new Vector2[xyMeshPointCount]; //記錄拓撲資訊迴圈的間隔 int triangleIndex = 0; for (int x = 0; x < xPointCount; x++) { for (int y = 0; y < yPointCount; y++) { int index = x + y * xPointCount; vertices[index] = new Vector3(x * mCellLen, 0, y * mCellLen); if (x < xCount && y < yCount) { //這裡就是拓撲資訊的迴圈計算,結合繪畫的拓撲資訊圖算一下 triangles[triangleIndex] = x + y * xPointCount; triangles[triangleIndex + 1] = x + (y + 1) * xPointCount; triangles[triangleIndex + 2] = x + (y + 1) * xPointCount + 1; triangles[triangleIndex + 3] = x + y * xPointCount; triangles[triangleIndex + 4] = x + (y + 1) * xPointCount + 1; triangles[triangleIndex + 5] = x + y * xPointCount + 1; triangleIndex += 6; } uvs[index] = new Vector2((float)x / (float)xCount, (float)y / (float)yCount); } } mMesh.vertices = vertices; mMesh.triangles = triangles; mMesh.uv = uvs; GetComponent<MeshFilter>().sharedMesh = mMesh; } }
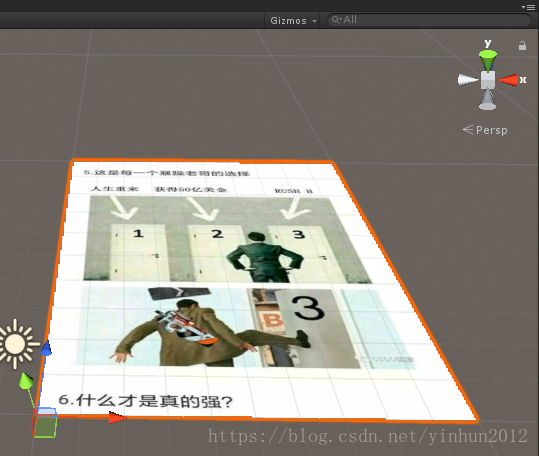
只在程式碼中進行了簡單的註釋,如果不理解的同學需要返回圖形輔助工具那一專欄學習,效果圖如下:
“書脊”座標系參照unity座標系。
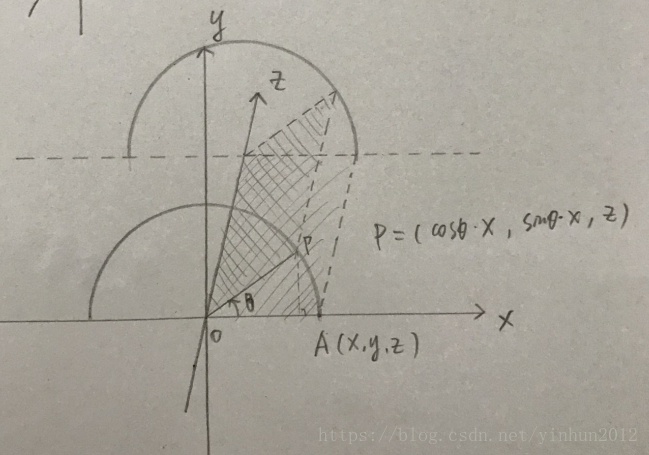
接著我們想象一下現實中翻書的效果,“書頁”沿著“書脊”的z軸進行逆時針180度運動,這個應該很簡單,使用z軸旋轉矩陣或者圓內sin cos函式就可以處理,這裡我要繪製一下方便理解,如下圖:
這裡我解釋一下,書頁OA經過逆時針θ角度的z軸旋轉運動,到達書頁OP,動點P座標為P(cosθ*X,sinθ*X,Z),當然假如小夥伴們看過我之前的三維旋轉矩陣部落格的話,同時也就知道使用z軸旋轉矩陣照樣能達到同樣的效果,那麼我們使用三角函式或者z軸旋轉矩陣進行定點變換處理不就完了?nonono,繼續往下看。
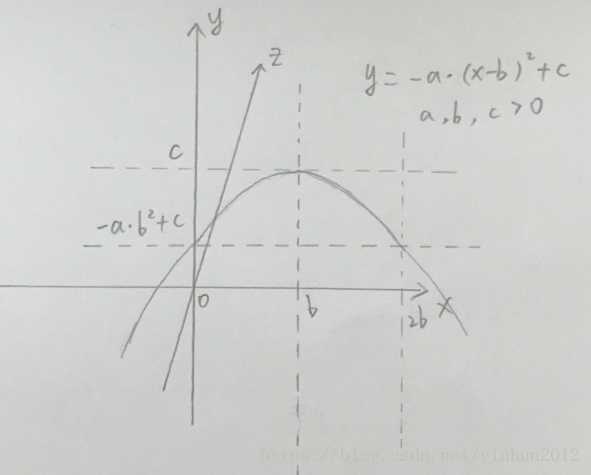
假如我們要模擬真實的“書頁”效果,就一個死板板直挺挺的旋轉根本不能滿足效果。想象一下,真實書頁翻動還會造成書頁的“扭曲”的,頁面可是一張薄薄的紙製品,翻動的時候會因為重力張力拉力等作用力產生弧線扭曲的效果,這個效果我們怎麼處理呢?不知道大家記不記得初中時候學習方程函式,一個普通的一元二次函式的函式影象就接近於書本開啟時拱起的弧度了,這裡我繪製一下y = -a*(x-b)^2+c(a,b,c>0)的函式影象,如下圖:
手繪弧線沒那麼精準,不過依舊看得出來,函式y = -a*(x-b)^2+c(a,b,c>0)通過調節a,b,c就可以達到讓頁面“彎曲”的效果,比如在進行三角函式sin cos進行“翻動的”同時,對頁面y軸座標進行y = -a*(x-b)^2+c(a,b,c>0)疊加處理,因為該方程函式具有對稱性,所以我們可以通過調節引數達到“頁面翻動”0-90度向“正面頁”拱起,頁面翻動90-180度向“背面頁”拱起的兩種對稱結果,就達到了現實中的效果,為了驗證一下我的猜想,實現程式碼如下:
Shader "Unlit/VertexFragUnlitShader"
{
Properties
{
_FrontTex ("FrontTexture", 2D) = "white" {}
_BackTex ("BackTexture",2D) = "white" {}
_Radian("Radian",Range(0.4,2.74)) = 0.4 //這裡使用弧度值,因為三角函式輸入為弧度
_Range("Range",Range(0.0,1.0)) = 0.01
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 100
Cull off //因為是書頁,所以正反面都需要顯示
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 frontuv : TEXCOORD0; /*記錄正面uv*/
float2 backuv : TEXCOORD1; /*記錄背面uv*/
float4 vertex : SV_POSITION;
};
sampler2D _FrontTex; /*書頁正面紋理*/
sampler2D _BackTex; /*書頁背面紋理*/
float4 _FrontTex_ST;
float4 _BackTex_ST;
float _Radian; /*翻動的弧度值*/
float _Range; /*翻書弧度的增幅值*/
v2f vert (appdata v)
{
v2f o;
//建立一個欄位用來處理頂點源座標資料
float4 zV;
//平面的x值根據翻動的弧度進行cos函數週期處理
zV.x = cos(_Radian)*v.vertex.x;
//平面的y值根據翻動的弧度進行sin函數週期處理
//同時,進行y = -a*x^2 + b*x + c的一元二次方程進行弧度拱起效果處理
zV.y = sin(_Radian)*v.vertex.x + _Range*(-pow((v.vertex.x-1),2)+1);
//平面的z值和w值就不需要改變了
zV.z = v.vertex.z;
zV.w = v.vertex.w;
//這裡再進行MATRIX_MVP變換處理,或者提前進行MVP處理一樣的
o.vertex = UnityObjectToClipPos(zV);
//對頁面正反貼圖的uv進行計算
o.frontuv = TRANSFORM_TEX(v.uv, _FrontTex);
o.backuv = TRANSFORM_TEX(v.uv,_BackTex);
//這裡注意,因為翻書翻過來以後,uv的x是反過來的,所以要用1.0-u
o.backuv.x = 1.0-o.backuv.x;
return o;
}
fixed4 frag (v2f i) : SV_Target
{
fixed4 col = fixed4(0.0,0.0,0.0,1.0);
//這裡就是控制當翻動的弧度達到0.5π的時候也就是角度90度時,就顯示頁面背面貼圖取樣,小於0.5π就進行正面貼圖取樣
if(_Radian<=1.57)
{
col = tex2D(_FrontTex, i.frontuv);
}
else{
col = tex2D(_BackTex, i.backuv);
}
return col;
}
ENDCG
}
}
}
程式碼中我做了簡單的註釋,這個CG shader程式碼我只著重強調兩點:
①.因為書頁是正反雙面都要顯示,所以使用兩張紋理貼圖,同時建立兩個紋理Texcoord欄位進行儲存,語義繫結到TEXCOORD0和TEXCOORD1(也就是儲存圖形流水線頂點階段後的紋理座標),當進行背面紋理uv計算時,記得x分量(或者u)是需要反向的也就是1.0-uv.x,才能在“翻到”背面時正常顯示背面的紋理,然後在fragment片段函式中判斷翻轉的弧度進行正反面取樣。
②.因為為了方便起見,我是用世界座標系原點進行變換處理,所以“翻頁”的時候處理使用cos(radian)*X處理x軸分量,sin(radian)*X + 調整後的方程函式處理y軸分量,z軸和w齊次擴充套件則不變,_Range為我額外加的一個效果增幅引數欄位,為了調整好效果,當然“書脊”所在的仿射座標系可以根據需要隨意translate位移,只是會多一步translate位移矩陣或者直接操作vertex.xyz分量還原而已。
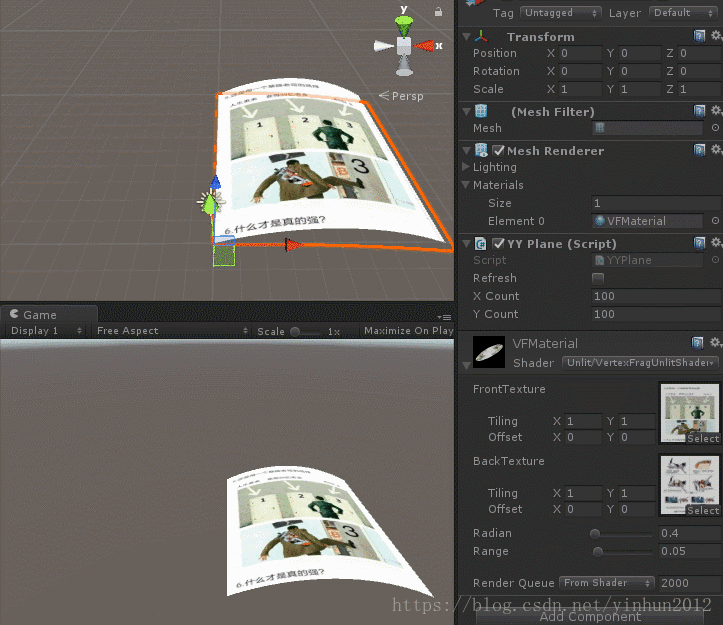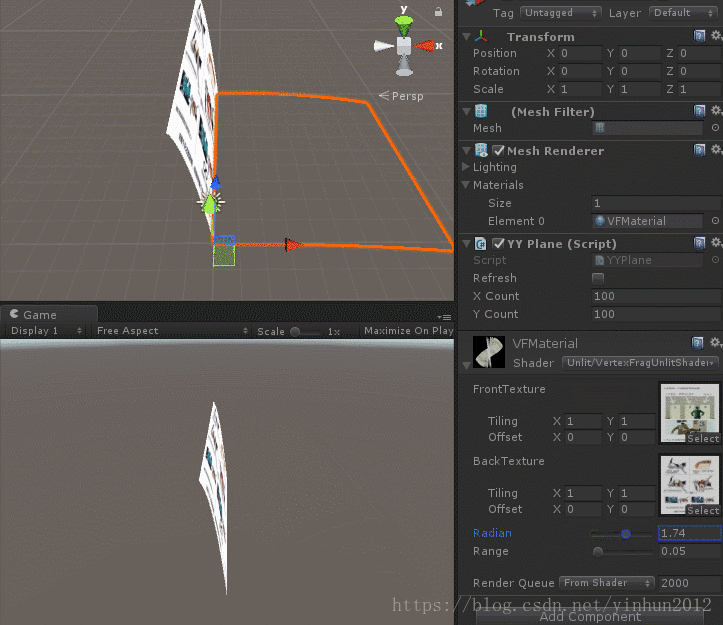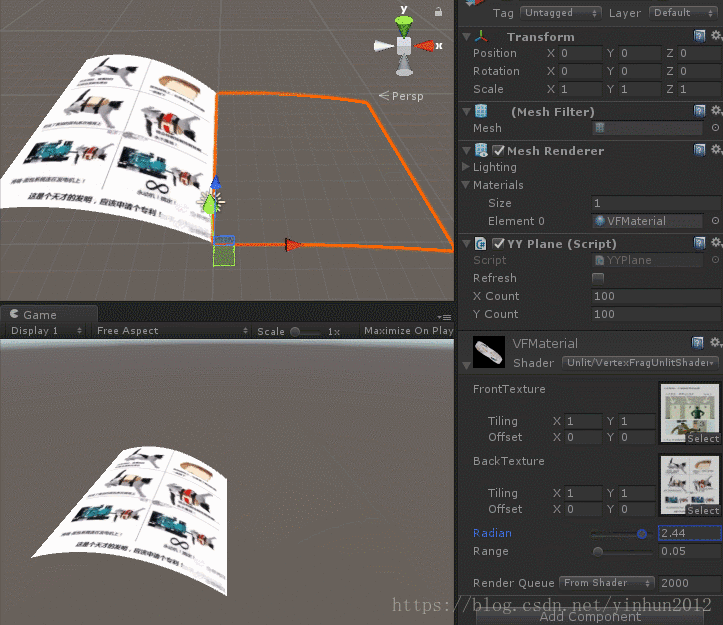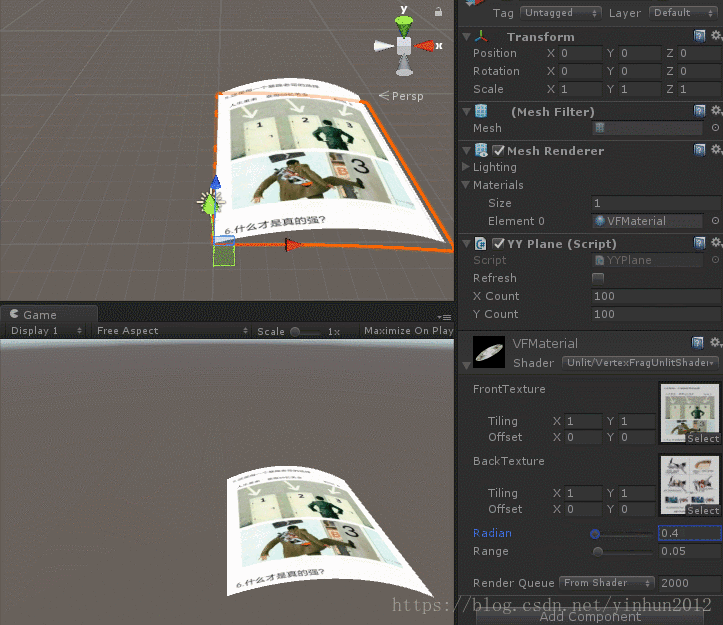
最後我們看下效果,如下圖:
當然翻書特效可以通過更復雜的函式影象去實現,到達非常符合現實的效果,這裡我只是做了一個簡單的CG shader來擴充套件學習到底著色器能幹些什麼稀奇古怪的事情,有興趣的小夥伴可以自己動手實現日常生活中一些自己喜歡的特效。
順便貼兩張“心理學”和“物理學”的圖片,如下:
so,我們接下來繼續。