畸變校正詳解

阿新 • • 發佈：2018-12-11

原創文章，歡迎轉載。轉載請註明：轉載自祥的部落格

1.攝像機成像原理簡述

成像的過程實質上是幾個座標系的轉換。首先空間中的一點由 世界座標系 轉換到 攝像機座標系 ，然後再將其投影到成像平面 ( 影象物理座標系 ) ，最後再將成像平面上的資料轉換到影象平面 ( 影象畫素座標系 ) 。

影象畫素座標系 (uOv座標系) 下的無畸變座標 (U, V)，經過 經向畸變 和 切向畸變 後落在了uOv座標系 的 (Ud, Vd) 上。即就是說，真實影象 imgR 與 畸變影象 imgD 之間的關係為: imgR(U, V) = imgD(Ud, Vd) 。

這裡寫圖片描述

2.成像畸變

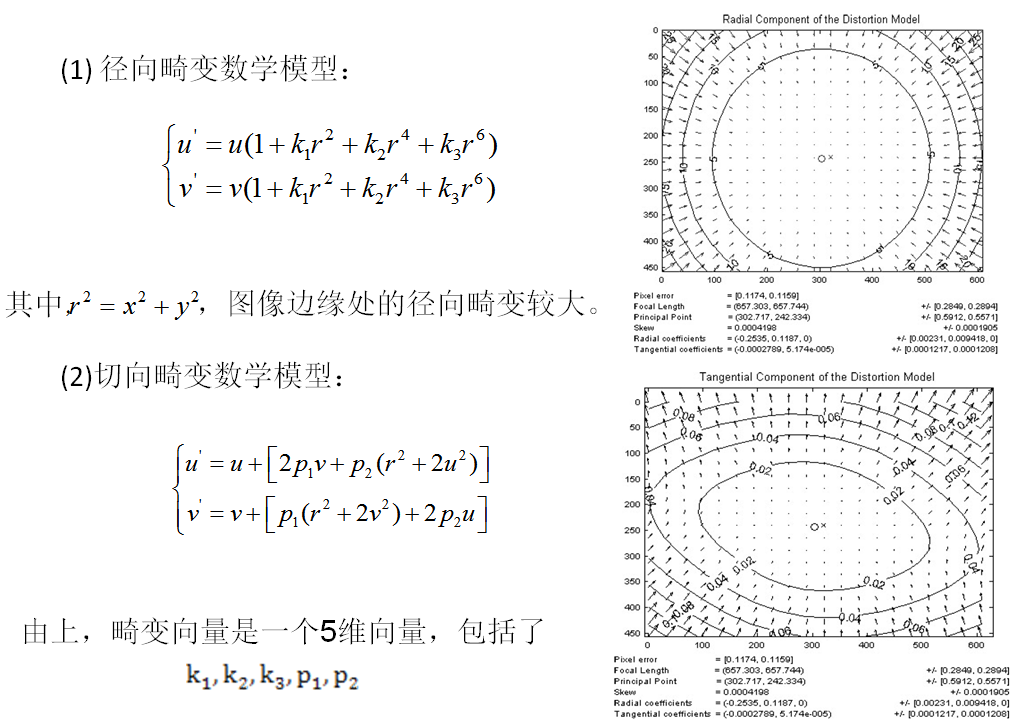
2.1. 畸變數學模型

攝像頭成像畸變的數學模型 (符合的對應關係有問題，可能會造成一些干擾，公式主要看後面推導的過程)

這裡寫圖片描述

2.2. 公式推導

公式推導:

這裡寫圖片描述

3.畸變校正

3.1. 理論推導

我們已知的是畸變後的影象，要得到沒有畸變的影象就要通過畸變模型推導其對映關係。 真實影象 imgR 與 畸變影象 imgD 之間的關係為: imgR(U, V) = imgD(Ud, Vd) 。通過這個關係，找出所有的 imgR(U, V) 。(U, V) 對映到 (Ud, Vd) 中的 (Ud, Vd) 往往不是整數 (U和V是整數，因為它是我們要組成影象的畫素座標位置，以這正常影象的座標位置去求在畸變影象中的座標位置，取出對應的畫素值，這也是正常影象的畫素值)

。但是畸變的畫素往往不是整數，所以需要通過插值來進行求解，詳細見我之前的部落格 [影象]影象縮放演算法-雙線性內插法。

這裡寫圖片描述

3.2. 程式碼實現


    clear;
    clc;
    A =[5.9418398977142772e+002 0 3.1950000000000000e+002;
        0    5.941839897714e+002 2.3950000000000000e+002;
        0 0 1];
    D = [6.7442695842244271e-002 2.4180872220967919e-001 0 0 -3.3970575589699975e-001];
    fx = A(1,1);
    fy = A(2,2);
    cx = A(1 
,3);
    cy = A(2,3);
    k1 = D(1);
    k2 = D(2);
    k3 = D(5);
    p1 = D(3);
    p2 = D(4);

    K = A;
    I_d = imread('img_d.png');
    I_d = rgb2gray(I_d);
    I_d = im2double(I_d);

    I_r = zeros(size(I_d));

    %影象座標系和矩陣的表示是相反的
    %[row,col] = find(X)，座標按照列的順序排列，這樣好和reshape()匹配出響應的影象矩陣
    [v u] = find(~isnan(I_r));

    % XYZc 攝像機座標系的值，但是已經歸一化了，因為沒有乘比例因子
    %公式 s[u v 1]' = A*[Xc Yc Zc]' ，其中s為比例因子，不加比例因子，Zc就為1，所以此時的Xc相對於( Xc/Zc )
    XYZc= inv(A)*[u v ones(length(u),1)]';

    % 此時的x和y是沒有畸變的
    r2 = XYZc(1,:).^2+XYZc(2,:).^2;
    x = XYZc(1,:);
    y = XYZc(2,:);

    % x和y進行畸變的
    x = x.*(1+k1*r2 + k2*r2.^2) + 2*p1.*x.*y + p2*(r2 + 2*x.^2);
    y = y.*(1+k1*r2 + k2*r2.^2) + 2*p2.*x.*y + p1*(r2 + 2*y.^2);

    % (u, v) 對應的畸變座標 (u_d, v_d)
    u_d = reshape(fx*x + cx,size(I_r));
    v_d = reshape(fy*y + cy,size(I_r));

    % 線性插值出非畸變的影象
    I_r = interp2(I_d, u_d, v_d);
    %對比影象
    subplot(121);     
        imagesc(I_d);
        title('畸變原影象');
    subplot(122);
        imagesc(I_r);
        title('校正後影象');

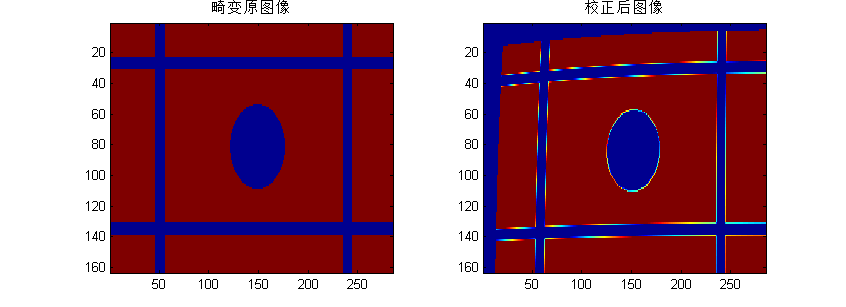
執行效果(攝像機內參是取網上的，圖也是自己畫的，影象本身沒有參考價值):

這裡寫圖片描述

畸變校正詳解

1.攝像機成像原理簡述