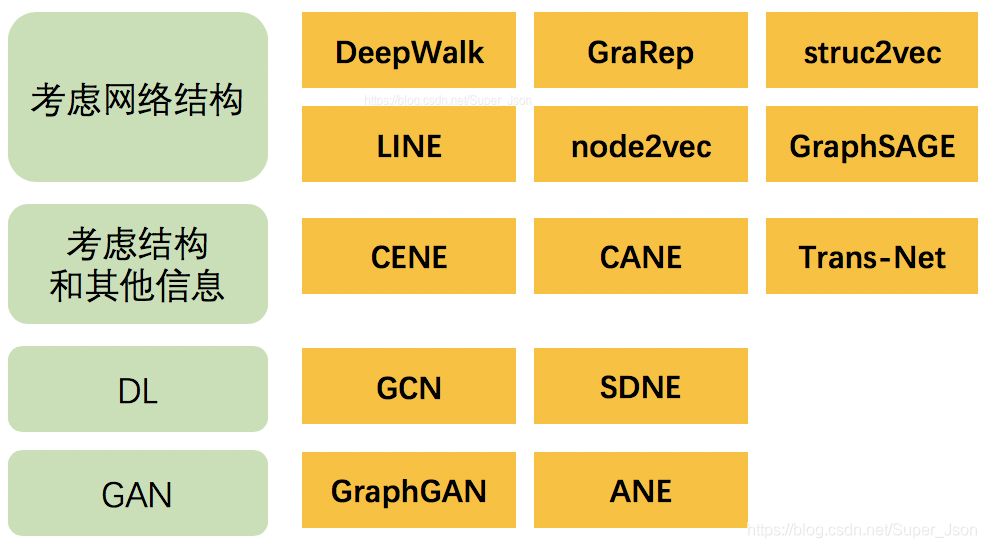
幾種常見的Graph Embedding方法
圖(Graph)是一個常見的資料結構,現實世界中有很多很多工可以抽象成圖問題,比如社交網路,蛋白體結構,交通路網資料,以及很火的知識圖譜等,甚至規則網路結構資料(如影象,視訊等)也是圖資料的一種特殊形式。針對graph的研究可以分成三類:1.簡單的graph演算法:如生成樹演算法,最短路演算法,複雜一點的二分圖匹配,費用流問題等等;2.概率圖模型:將條件概率表達為圖結構,並進一步挖掘,典型的有條件隨機場等;3.圖神經網路:研究圖結構資料探勘的問題,典型的有graph embedding,graph CNN等。
總覽
在介紹Graph Embedding之前,我們先回顧什麼是Embedding?Embedding在數學上是一個函式,將一個空間的點對映到另一個空間,通常是從高維抽象的空間對映到低維的具象空間。
最常見的embeding方法是word2vec,根據語料庫中單詞的共現關係求出每個單詞的embedding,常用的word2vec模型有cbow和skip-gram兩種,cbow根據上下文預測中心詞,skip-gram根據中心詞預測上下文(詳見word2vec 中的數學原理詳解)。因此既然自然語言中的單詞可以通過共現關係進行embedding,那麼將graph類比成整個語料庫,圖中的節點類比成單詞,我們是否也可以通過共現關係對graph中的node進行embedding?對於word2vec而言,語料庫中的每個句子都可以描述單詞之間的共現,對於graph,這種共現關係如何描述呢?接下來我們將對多種不同的graph embedding方式進行展開。
Graph Embedding
由於資訊網路可能包含數十億個節點和邊緣,因此在整個網路上執行復雜的推理過程可能會非常棘手。因此有人提出了用於解決該問題的一種方法是網路嵌入(Network Embedding)。NE 的中心思想就是找到一種對映函式,該函式將網路中的每個節點轉換為低維度的潛在表示。
總的來說,NE 具有如下幾個特徵:
適應性(Adaptability)- 現實的網路在不斷髮展;新的應用演算法不應該要求不斷地重複學習過程。
可擴充套件性(Scalability)- 真實網路本質上通常很大,因此網路嵌入演算法應該能夠在短時間內處理大規模網路。
社群感知(Community aware)- 潛在表示之間的距離應表示用於評估網路的相應成員之間的相似性的度量。這就要求同質網路能夠泛化。
低維(Low dimensional)- 當標記資料稀缺時,低維模型更好地推廣並加速收斂和推理。
持續(Continuous)- 需要潛在的表示來模擬連續空間中的部分社群成員資格。
一個典型的例子就是 DeepWalk。其學習 Zachary’s Karate network 網路中的拓撲結構資訊並轉換成一個二維的潛在表示(latent representation)。
圖嵌入,即用一個低維,稠密的向量去表示圖中的點,該向量表示能反映圖中的結構,本質上就是說,兩個點其共享的(n階)鄰近點越多,即兩個點的上下文越相似,兩個對應向量距離越近。而圖嵌入的最大好處自然是得到的向量表示可以輸入任何的機器學習模型去解決具體面對的問題。同時對比一些傳統的方法有對應的優勢,比如基於矩陣分解(MF)的方法計算量太大;構造人工特徵需要領域知識和較大的工作量。
圖嵌入可用於推薦,節點分類,連結預測(link prediction),視覺化等場景
Network Embedding 簡史
傳統意義上的 Graph Embedding 被看成是一個降維的過程,而主要的方法包括主成分分析(PCA)和多維縮放(MDS)。所有的方法都可以理解成運用一個 n × k 的矩陣來表示原始的 n × m 矩陣,其中 k << n。
在 2000 年代早期,又提出了其他方法,如 IsoMap 和 LLE,以保持非線性流形的整體結構。總的來說,這些方法都在小型網路上提供了良好的效能。 然而這些方法的時間複雜性至少是二次的,這使得它們無法在大規模網路上執行。
另一類流行的降維技術使用可從圖中匯出的矩陣的光譜特性(例如,特徵向量)來嵌入圖的節點。拉普拉斯特徵對映(Laplacian eigenmaps)通過與其k個最小非平凡特徵值相關聯的特徵向量表示圖中的每個節點。
Deep Learning
DeepWalk [1] 是第一個被提出來使用表示學習(或深度學習)社群的技術的網路嵌入方法。DeepWalk 通過將節點視為單詞並生成短隨機遊走作為句子來彌補網路嵌入和單詞嵌入之間的差距。然後,可以將諸如 Skip-gram 之類的神經語言模型應用於這些隨機遊走以獲得網路嵌入。
DeepWalk 的優點可以概括為:首先其可以按需生成隨機遊走。由於 Skip-gram 模型也針對每個樣本進行了優化,因此隨機遊走和 Skip-gram 的組合使 DeepWalk 成為線上演算法。其次,DeepWalk 是可擴充套件的,生成隨機遊走和優化 Skip-gram 模型的過程都是高效且平凡的並行化。最重要的是,DeepWalk 引入了深度學習圖形的範例。

Unsupervised Network Embeddings
1.deepwalk
Deepwalk[2014] : DeepWalk: online learning of social representations
2.node2vec(Scalable Feature Learning for Networks)
node2vec在DW的基礎上,定義了一個bias random walk的策略生成序列,仍然用skip gram去訓練。
論文分析了BFS和DFS兩種遊走方式,保留的網路結構資訊是不一樣的。 DeepWalk中根據邊的權重進行隨機遊走,而node2vec加了一個權重調整引數α:t是上一個節點,v是最新節點,x是候選下一個節點。d(t,x)是t到候選節點的最小跳數。 通過不同的p和q引數設定,來達到保留不同資訊的目的。當p和q都是1.0的時候,它等價於DeepWalk。
這篇文章來自於Jure Leskovec的組。文章所提出的方法軟體實現。
文章的主要想法就是,利用SkipGram的方法,來為Networks抽取Representation。那麼,自然,根據SkipGram的思路,最重要的就是定義這個Context,或者說是Neighborhood。從文字的角度來說,這個Neighborhood當然就是當前Word周圍的字,這個定義非常自然。但是對於Graph或者Network來說就來得沒那麼容易了。
文章闡述了一般所採用Depth-First Search或者是Breadth-First Search來Sample一個Node的周邊Node的問題。簡單來說,BFS比較容易有一個Microscopic的View而DFS容易有一個Macro-view,兩者都有Representative的問題。
文章的核心思想是採用Random Walk來代替DFS或者BFS。文章定義了一種二階的Random Walk,擁有兩個引數,來控制多大的概率反覆經過一些Node和控制所謂的Inward和Outward。總之,整個Random Walk的目的就是在DFS和BFS之間採取某種平衡。
文章雖然提出的是關於Node Feature提取的演算法,但是Edge Feature也可以很容易從Node Feature匯出。
總體感覺是,硬要用SkipGram或者WordVec的想法在Networks上做,還顯得比較牽強。因為有這個Neighborhood的概念,在Graph上,反而不是那麼直觀得定義,因此所有類似的工作都顯得比較彆扭。當然,這篇文章也不失為一種不錯的Heuristic。
具體應用可以參考騰訊lookalike演算法。
3.
