紅黑樹屬於二叉搜尋樹，但是每個節點增加了一個存顏色的位，它的規則是： 1.根節點為黑色。 2.不能有連續的兩個紅節點，所以如果一個節點的顏色為紅，那麼它的子節點若不為空則一定為紅。 3.每條路徑上黑節點數量相同。 所以保證了最長路徑不超過最短路徑的兩倍，沒有AVL樹那麼嚴格的平衡，但是旋轉少效率高，也是O(LgN）。

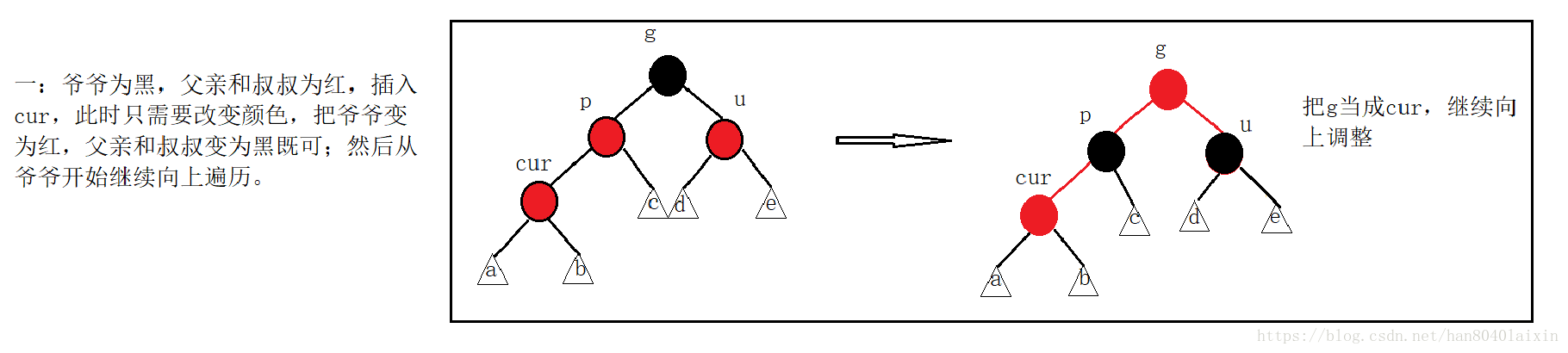
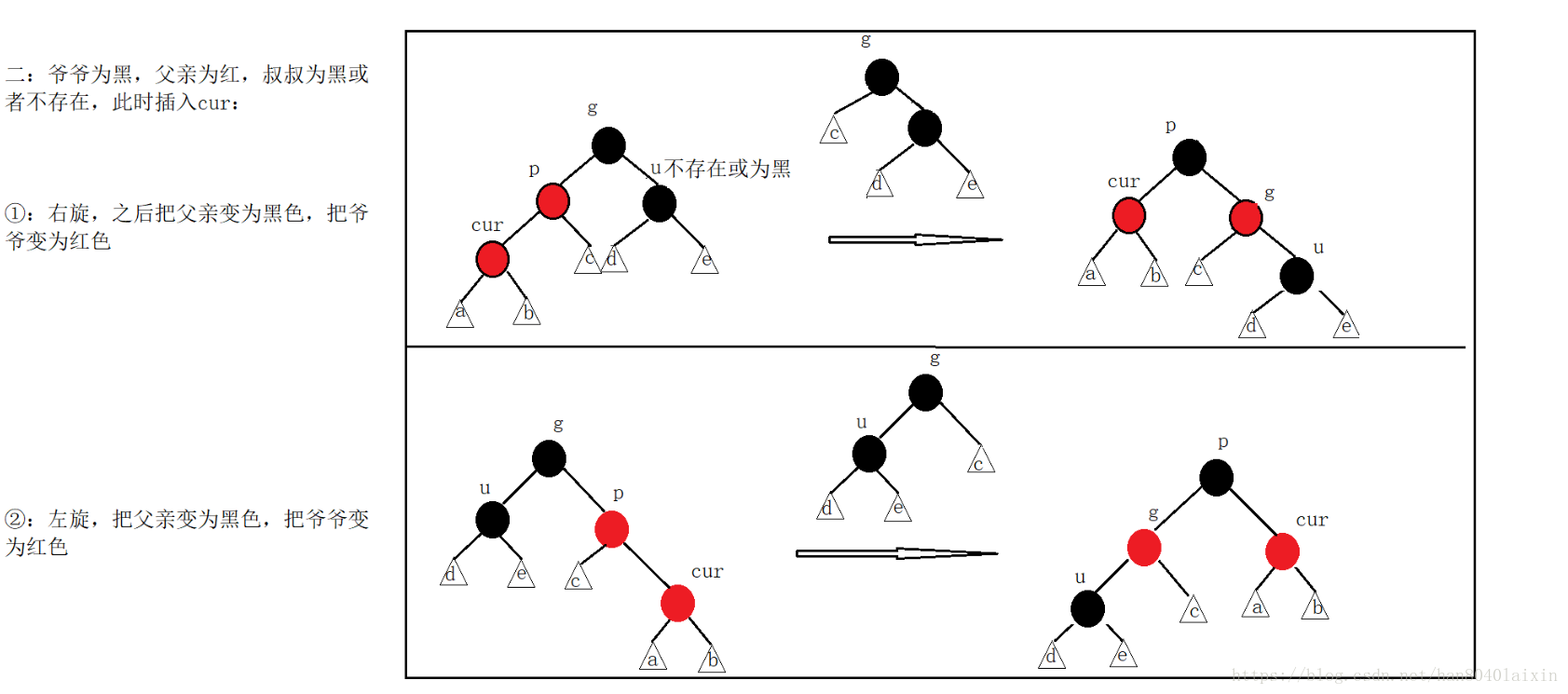
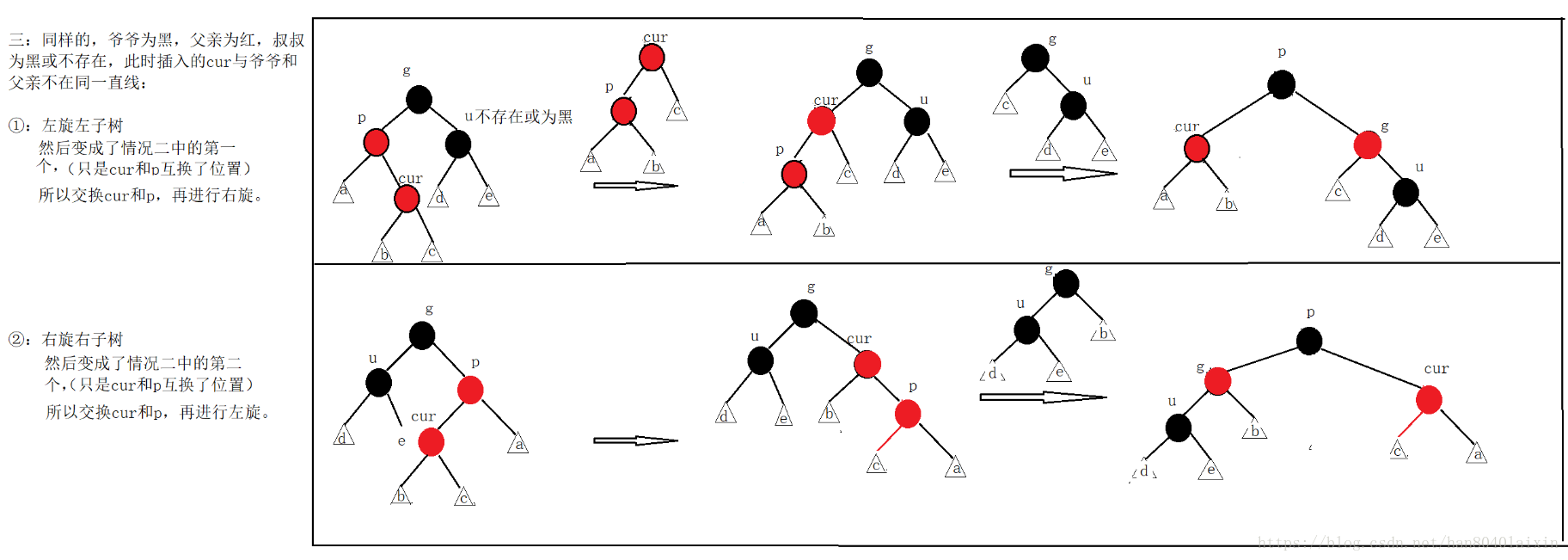
判斷一棵樹是否為紅黑樹：

	bool IsRB()
	{
		if (_root != NULL && _root->_col == RED)//根為紅則不是紅黑樹
			return false;

		int CurBlackNum = 0;//用來記錄每路的黑節點個數

		int BlackNum = 0;//先統計出一條路徑的黑色節點的個數
		Node* cur = _root;
		while (cur)
		{
			if (cur->_col == BLACK)
				BlackNum++;
			cur = cur->_left;
		}

		return _IsRB(_root, BlackNum, CurBlackNum);
	}

	bool _IsRB(Node* root, int BlackNum, int CurBlackNum)
	{
		if (root == NULL)
			return true;

		if (root->_col == RED && root->_parent->_col == RED)//兩個連續的紅節點則不為紅黑樹
			return false;

		if (root->_col == BLACK)//黑節點就將CurBlackNum++
			CurBlackNum++;

		if (root->_left == NULL && root->_right == NULL)
		{
			if (CurBlackNum == BlackNum)
				return true;
			else//黑色節點不相等返回false
				return false;
		}

		return _IsRB(root->_left, BlackNum, CurBlackNum)
			&& _IsRB(root->_right, BlackNum, CurBlackNum);//和AVL一樣，再判斷左子樹和右子樹
	}