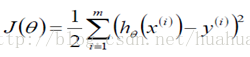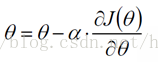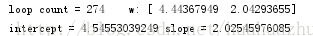梯度下降（Gradient Descent）演算法是機器學習中使用非常廣泛的優化演算法。當前流行的機器學習庫或者深度學習庫都會包括梯度下降演算法的不同變種實現。

本文主要以線性迴歸演算法損失函式求極小值來說明如何使用梯度下降演算法並給出python實現。若有不正確的地方，希望讀者能指出。

• 梯度下降

梯度下降原理：將函式比作一座山，我們站在某個山坡上，往四周看，從哪個方向向下走一小步，能夠下降的最快。

線上性迴歸演算法中，損失函式為

在求極小值時，在資料量很小的時候，可以使用矩陣求逆的方式求最優的θ值。但當資料量和特徵值非常大，例如幾萬甚至上億時，使用矩陣求逆根本就不現實。而梯度下降法就是很好的一個選擇了。

使用梯度下降演算法的步驟：

1）對θ賦初始值，這個值可以是隨機的，也可以讓θ是一個全零的向量。

其中為學習率或步長，需要人為指定，若過大會導致震盪即不收斂，若過小收斂速度會很慢。

3）當下降的高度小於某個定義的值，則停止下降。

另外，對上面線性迴歸演算法損失函式求梯度，結果如下：

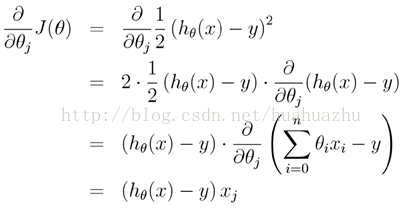
在實際應用的過程中，梯度下降演算法有三類，它們不同之處在於每次學習(更新模型引數)使用的樣本個數，每次更新使用不同的樣本會導致每次學習的準確性和學習時間不同。下面將分別介紹原理及python實現。

• 批量梯度下降(Batch gradient descent) 

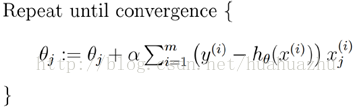
梯度下降演算法最終得到的是區域性極小值。而線性迴歸的損失函式為凸函式，有且只有一個區域性最小，則這個區域性最小一定是全域性最小。所以線性迴歸中使用批量梯度下降演算法，一定可以找到一個全域性最優解。

優點：全域性最優解；易於並行實現；總體迭代次數不多缺點：當樣本數目很多時，訓練過程會很慢，每次迭代需要耗費大量的時間。

• 隨機梯度下降(Stochastic gradient descent)

隨機梯度下降演算法每次從訓練集中隨機選擇一個樣本來進行迭代，即：

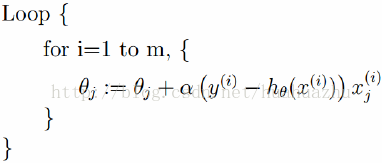
隨機梯度下降演算法每次只隨機選擇一個樣本來更新模型引數，因此每次的學習是非常快速的，並且可以進行線上更新。 

隨機梯度下降最大的缺點在於每次更新可能並不會按照正確的方向進行，因此可以帶來優化波動(擾動)。不過從另一個方面來看，隨機梯度下降所帶來的波動有個好處就是，對於類似盆地區域（即很多區域性極小值點）那麼這個波動的特點可能會使得優化的方向從當前的區域性極小值點跳到另一個更好的區域性極小值點，這樣便可能對於非凸函式，最終收斂於一個較好的區域性極值點，甚至全域性極值點。 

優點：訓練速度快，每次迭代計算量不大缺點：準確度下降，並不是全域性最優；不易於並行實現；總體迭代次數比較多。

• Mini-batch梯度下降演算法

Mini-batch梯度下降綜合了batch梯度下降與stochastic梯度下降，在每次更新速度與更新次數中間取得一個平衡，其每次更新從訓練集中隨機選擇b,b<m個樣本進行學習，即：

========================================================================================================================================================================================================================================================================

====python程式碼實現====================================================================================================================

批量梯度下降演算法

#!/usr/bin/python
#coding=utf-8
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
# 構造訓練資料
x = np.arange(0., 10., 0.2)
m = len(x)  # 訓練資料點數目
print m
x0 = np.full(m, 1.0)
input_data = np.vstack([x0, x]).T  # 將偏置b作為權向量的第一個分量
target_data = 2 * x + 5 + np.random.randn(m)
# 兩種終止條件
loop_max = 10000  # 最大迭代次數(防止死迴圈)
epsilon = 1e-3
# 初始化權值
np.random.seed(0)
theta = np.random.randn(2)
alpha = 0.001  # 步長(注意取值過大會導致振盪即不收斂,過小收斂速度變慢)
diff = 0.
error = np.zeros(2)
count = 0  # 迴圈次數
finish = 0  # 終止標誌
while count < loop_max:
    count += 1
    # 標準梯度下降是在權值更新前對所有樣例彙總誤差，而隨機梯度下降的權值是通過考查某個訓練樣例來更新的
    # 在標準梯度下降中，權值更新的每一步對多個樣例求和，需要更多的計算
    sum_m = np.zeros(2)
    for i in range(m):
        dif = (np.dot(theta, input_data[i]) - target_data[i]) * input_data[i]
        sum_m = sum_m + dif  # 當alpha取值過大時,sum_m會在迭代過程中會溢位
    theta = theta - alpha * sum_m  # 注意步長alpha的取值,過大會導致振盪
    # theta = theta - 0.005 * sum_m      # alpha取0.005時產生振盪,需要將alpha調小
    # 判斷是否已收斂
    if np.linalg.norm(theta - error) < epsilon:
        finish = 1
        break
    else:
        error = theta
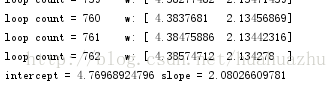
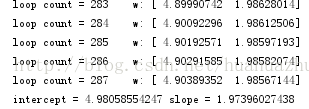
    print 'loop count = %d' % count, '\tw:',theta
print 'loop count = %d' % count, '\tw:',theta
# check with scipy linear regression
slope, intercept, r_value, p_value, slope_std_error = stats.linregress(x, target_data)
print 'intercept = %s slope = %s' % (intercept, slope)
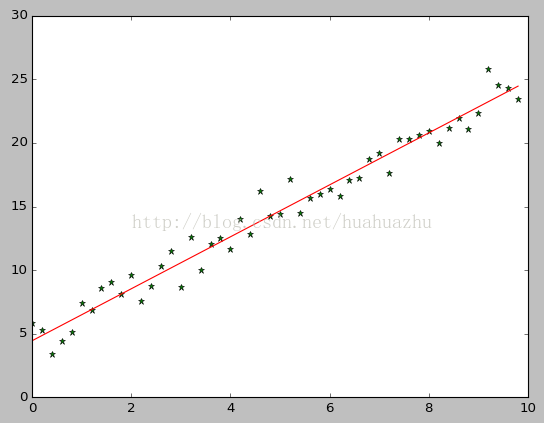
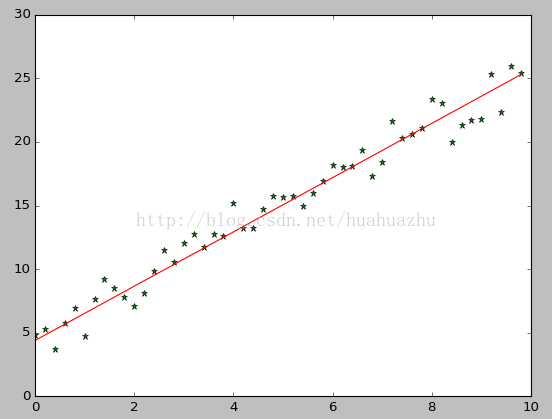
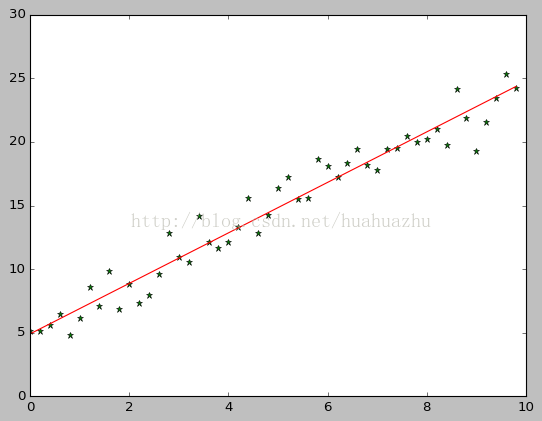
plt.plot(x, target_data, 'g*')
plt.plot(x, theta[1] * x + theta[0], 'r')
plt.show()

隨機梯度下降演算法

#!/usr/bin/python
#coding=utf-8
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
# 構造訓練資料
x = np.arange(0., 10., 0.2)
m = len(x)  # 訓練資料點數目
x0 = np.full(m, 1.0)
input_data = np.vstack([x0, x]).T  # 將偏置b作為權向量的第一個分量
target_data = 2 * x + 5 + np.random.randn(m)
# 兩種終止條件
loop_max = 10000  # 最大迭代次數(防止死迴圈)
epsilon = 1e-3
# 初始化權值
np.random.seed(0)
theta = np.random.randn(2)
# w = np.zeros(2)
alpha = 0.001  # 步長(注意取值過大會導致振盪,過小收斂速度變慢)
diff = 0.
error = np.zeros(2)
count = 0  # 迴圈次數
finish = 0  # 終止標誌
######-隨機梯度下降演算法
while count < loop_max:
    count += 1
    # 遍歷訓練資料集，不斷更新權值
    for i in range(m):
        diff = np.dot(theta, input_data[i]) - target_data[i]  # 訓練集代入,計算誤差值
        # 採用隨機梯度下降演算法,更新一次權值只使用一組訓練資料
        theta = theta - alpha * diff * input_data[i]
        # ------------------------------終止條件判斷-----------------------------------------
        # 若沒終止，則繼續讀取樣本進行處理，如果所有樣本都讀取完畢了,則迴圈重新從頭開始讀取樣本進行處理。
    # ----------------------------------終止條件判斷-----------------------------------------
    # 注意：有多種迭代終止條件，和判斷語句的位置。終止判斷可以放在權值向量更新一次後,也可以放在更新m次後。
    if np.linalg.norm(theta - error) < epsilon:     # 終止條件：前後兩次計算出的權向量的絕對誤差充分小
        finish = 1
        break
    else:
        error = theta
print 'loop count = %d' % count,  '\tw:',theta
# check with scipy linear regression
slope, intercept, r_value, p_value, slope_std_error = stats.linregress(x, target_data)
print 'intercept = %s slope = %s' % (intercept, slope)
plt.plot(x, target_data, 'g*')
plt.plot(x, theta[1] * x + theta[0], 'r')
plt.show()

執行結果截圖：

Mini-batch梯度下降

#!/usr/bin/python
#coding=utf-8
import numpy as np
from scipy importstats
import matplotlib.pyplot as plt
# 構造訓練資料
x = np.arange(0.,10.,0.2)
m = len(x)  # 訓練資料點數目
print m
x0 = np.full(m, 1.0)
input_data = np.vstack([x0, x]).T  # 將偏置b作為權向量的第一個分量
target_data = 2 *x + 5 +np.random.randn(m)
# 兩種終止條件
loop_max = 10000  #最大迭代次數(防止死迴圈)
epsilon = 1e-3
# 初始化權值
np.random.seed(0)
theta = np.random.randn(2)
alpha = 0.001  #步長(注意取值過大會導致振盪即不收斂,過小收斂速度變慢)
diff = 0.
error = np.zeros(2)
count = 0  #迴圈次數
finish = 0  #終止標誌
minibatch_size = 5  #每次更新的樣本數
while count < loop_max:
    count += 1
    # minibatch梯度下降是在權值更新前對所有樣例彙總誤差，而隨機梯度下降的權值是通過考查某個訓練樣例來更新的
    # 在minibatch梯度下降中，權值更新的每一步對多個樣例求和，需要更多的計算
    for i inrange(1,m,minibatch_size):
        sum_m = np.zeros(2)
        for k inrange(i-1,i+minibatch_size-1,1):
            dif = (np.dot(theta, input_data[k]) - target_data[k]) *input_data[k]
            sum_m = sum_m + dif  #當alpha取值過大時,sum_m會在迭代過程中會溢位
        theta = theta- alpha * (1.0/minibatch_size) * sum_m #注意步長alpha的取值,過大會導致振盪
    # 判斷是否已收斂
    if np.linalg.norm(theta- error) < epsilon:
        finish = 1
        break
    else:
        error = theta
    print 'loopcount = %d'% count, '\tw:',theta
print 'loop count = %d'% count, '\tw:',theta
# check with scipy linear regression
slope, intercept, r_value, p_value,slope_std_error = stats.linregress(x, target_data)
print 'intercept = %s slope = %s'% (intercept, slope)
plt.plot(x, target_data, 'g*')
plt.plot(x, theta[1]* x +theta[0],'r')
plt.show()

執行結果：