排序【5.1】桶排序&&基數排序&&計數排序
1、桶排序(Bucket Sort)
(1)基本思想
桶排序的基本思想是將一個數據表分割成許多buckets,然後每個bucket各自排序,或用不同的排序演算法,或者遞迴的使用bucket sort演算法。也是典型的divide-and-conquer分而治之的策略。它是一個分散式的排序,介於MSD基數排序和LSD基數排序之間。
(2)基本流程
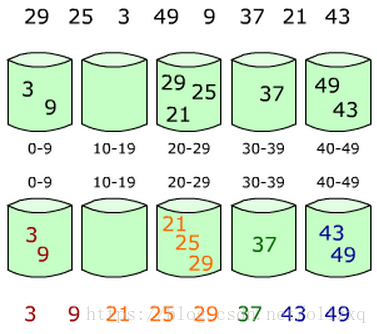
建立一堆buckets; 遍歷原始陣列,並將資料放入到各自的buckets當中; 對非空的buckets進行排序; 按照順序遍歷這些buckets並放回到原始陣列中即可構成排序後的陣列。
圖示
(3)演算法複雜度
桶排序利用函式的對映關係,減少了幾乎所有的比較工作。實際上,桶排序的f(k)值的計算,其作用就相當於快排中劃分,已經把大量資料分割成了基本有序的資料塊(桶)。然後只需要對桶中的少量資料做先進的比較排序即可。
對N個關鍵字進行桶排序的時間複雜度分為兩個部分:
(1) 迴圈計算每個關鍵字的桶對映函式,這個時間複雜度是。
(2) 利用先進的比較排序演算法對每個桶內的所有資料進行排序,其時間複雜度為 。其中為第i個桶的資料量。
很顯然,
第(2)部分是桶排序效能好壞的決定因素。儘量減少桶內資料的數量是提高效率的唯一辦法(因為基於比較排序的最好平均時間複雜度只能達到O(N*logN)了。因此,我們需要儘量做到下面兩點:
(1) 對映函式f(k)能夠將N個數據平均的分配到M個桶中,這樣每個桶就有[N/M]
對於N個待排資料,M個桶,平均每個桶[N/M]個數據的桶排序平均時間複雜度為: 當N=M時,即極限情況下每個桶只有一個數據時。桶排序的最好效率能夠達到O(N)。
總結:桶排序的平均時間複雜度為線性的O(N+C),其中C=N*(logN-logM)。如果相對於同樣的N,桶數量M越大,其效率越高,最好的時間複雜度達到O(N)。當然桶排序的空間複雜度為O(N+M),如果輸入資料非常龐大,而桶的數量也非常多,則空間代價無疑是昂貴的。此外,桶排序是穩定的。
(4)演算法實現(python3)
"""
桶排序:
基本思想:
將一個數據表分割成許多buckets,然後每個bucket各自排序,或用不同的排序演算法,或者遞迴的使用bucket sort演算法。
也是典型的divide-and-conquer分而治之的策略。它是一個分散式的排序。
時間複雜度:O(N)+O(M*(N/M)*log(N/M)) = O(N+N*(logN-logM)) = O(N+N*logN-N*logM)
"""
class node(object):
def __init__(self, initdata):
self.data = initdata
self.next = None
def getBucketIndex(value):
return value//interval
def printBuckets(bucket):
cur = bucket
while cur:
print(cur.data, " ",end = "")
cur = cur.next
print("\n")
def bucketSort(data):
bucket = []
for i in range(n_bucket):
bucket.append(None)
for i in range(n_data):
pos = getBucketIndex(data[i]) # O(N) + O(M)
current = node(data[i])
cur = bucket[pos]
# 比較排序
if cur == None or cur.data > current.data: # O(N/Mlog(N/M))
current.next = cur
bucket[pos] = current
bucket[pos] = current
else:
last = cur
while cur != None and cur.data < current.data:
last = cur
cur = cur.next
current.next = cur
last.next = current
for i in range(n_bucket):
print("Bucket[", i,"] : ", end = "")
printBuckets(bucket[i])
result = []
for i in range(n_bucket):
cur = bucket[i]
while cur is not None:
result.append(cur.data)
cur = cur.next
return result
if __name__ == '__main__':
data = [20, 40, 30, 10, 80, 50, 60, 90]
n_data = len(data) # data size
n_bucket = 5 # bucket size
interval = 20 # bucket range
print("before sort:", data)
data_order = bucketSort(data)
print("after sort:", data_order)
輸出結果:
before sort: [20, 40, 30, 10, 80, 50, 60, 90]
Bucket[ 0 ] : 10
Bucket[ 1 ] : 20 30
Bucket[ 2 ] : 40 50
Bucket[ 3 ] : 60
Bucket[ 4 ] : 80 90
after sort: [10, 20, 30, 40, 50, 60, 80, 90]
2、基數排序(Radix Sort)
(1)基本思想:
基數排序(Radix Sort)是桶排序的擴充套件,它的基本思想是:將整數按位數切割成不同的數字,然後按每個位數分別比較。
具體做法是: 將所有待比較數值統一為同樣的數位長度,數位較短的數前面補零。然後,從最低位開始,依次進行一次排序。這樣從最低位排序一直到最高位排序完成以後, 數列就變成一個有序序列。
(2)排序過程:
通過基數排序對陣列{53, 3, 542, 748, 14, 214, 154, 63, 616},它的示意圖如下:
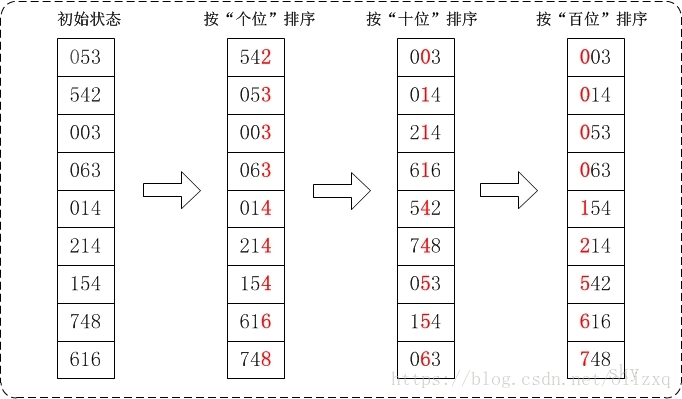
- 按照個位數進行排序。
- 按照十位數進行排序。
- 按照百位數進行排序。
排序後,數列就變成了一個有序序列。
radix_sort(a, n)的作用是對陣列a進行排序:
- 首先通過get_max(a)獲取陣列a中的最大值。獲取最大值的目的是計算出陣列a的最大指數。
- 獲取到陣列a中的最大指數之後,再從指數1開始,根據位數對陣列a中的元素進行排序。排序的時候採用了桶排序。
- count_sort(a, n, exp)的作用是對陣列a按照指數exp進行排序。 下面簡單介紹一下對陣列{53, 3, 542, 748, 14, 214, 154, 63, 616}按個位數進行排序的流程。
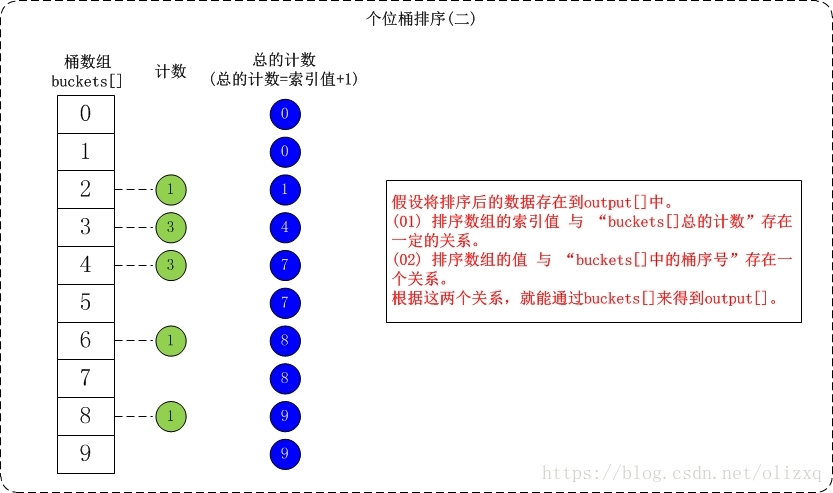
(01) 個位的數值範圍是[0,10)。因此,參見桶陣列buckets[],將陣列按照個位數值新增到桶中。
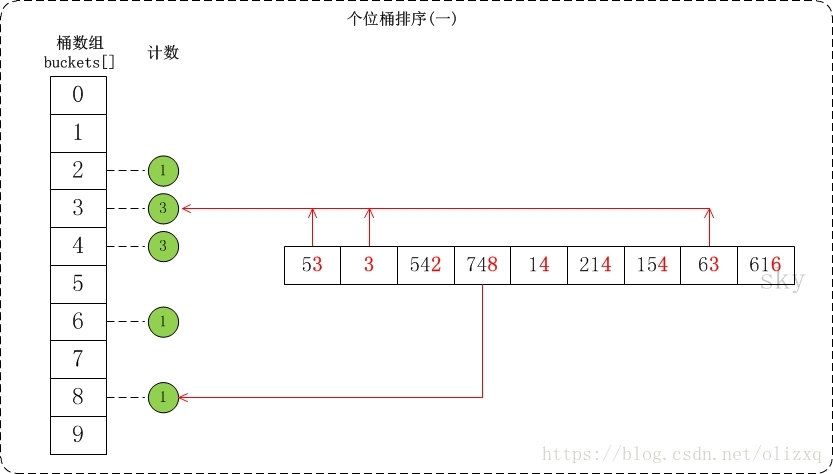
(3)複雜度分析:
空間
空間採用順序分配,顯然不合適,由於每個口袋都有可能存放所有的待排序的整數,所以,額外空間的需求為10n,太大了。
採用連結串列分配是合理的,額外空間的需求為n,通常再增加指向每個口袋的首尾指標就可以了。在一般情況下,設每個關鍵字的取值範圍為radix, 首尾指標共計2×radix個,總的空間為O(n+2×radix)。
時間
如果每個數共有2位,因此執行2次分配和收集就可以了。在一般情況下,每個結點有d位關鍵字,必須執行d次分配和收集操作。
• 每次分配的代價:O(n)
• 每次收集的代價:O(radix)
• 總的代價為:O(d×(n+radix))
(4)演算法實現(python3)
"""
基數排序:
基本思想:
基數排序(Radix Sort)是桶排序的擴充套件,它的基本思想是:將整數按位數切割成不同的數字,然後按每個位數分別比較。
時間複雜度:O(d(n+r))
"""
def countSort(data, exp):
data_order = [0] * len(data)
# 初始化計數陣列
count_arr = [0] * ((max(data) - min(data)) + 1)
# 統計i的次數
for i in range(len(data)): # O(n)
count_arr[((data[i] - min(data))//exp)%10] += 1
# 對所有的計數累加
for i in range(len(count_arr)-1): # O(r) r表示基數,本例中為10
count_arr[i+1] += count_arr[i]
# 逆向遍歷源陣列(保證穩定性),根據計數陣列中對應的值填充到先的陣列中
for i in range(len(data)-1, -1, -1): # O(n)
data_order[count_arr[((data[i] - min(data))//exp)%10]-1] = data[i]
count_arr[((data[i] - min(data)) // exp) % 10] -= 1
for i in range(len(data)): # O(n)
data[i] = data_order[i]
def getMax(data):
max = data[0]
for i in range(len(data)):
if data[i] > max:
max = data[i]
return max
def radixSort(data):
exp = 1
max = getMax(data)
while max/exp > 0: # O(d) d表示最大數的長度
countSort(data, exp)
exp *= 10
if __name__ == '__main__':
data = [234, 48, 76, 10, 98, 1, 237, 227]
print("before sort:", data)
radixSort(data)
print("after sort:", data)
執行結果:
before sort: [234, 48, 76, 10, 98, 1, 237, 227]
after sort: [1, 10, 48, 76, 98, 227, 234, 237]
3、計數排序(Counting Sort)
目前介紹的利用比較元素進行排序的方法對資料表長度為n的資料表進行排序時間複雜度不可能低於O(nlogn)。但是如果知道了一些資料表的資訊,那麼就可以實現更為獨特的排序方式,甚至是可以達到線性時間的排序。
它是一個不需要比較的,類似於桶排序的線性時間排序演算法。該演算法是對已知數量範圍的陣列進行排序。其時間複雜度為O(n),適用於小範圍集合的排序。計數排序是用來排序0到100之間的數字的最好的演算法。
比如100萬學生參加高考,我們想對這100萬學生的數學成績(假設分數為0到100)做個排序。
(1)基本思想:
當資料表長度為n,已知資料表中資料的範圍有限,比如在範圍0−k之間,而k又比n小許多,這樣可以通過統計每一個範圍點上的資料頻次來實現計數排序。
(2)排序過程:
總體思路:
根據獲得的資料表的範圍,分割成不同的buckets,然後直接統計資料在buckets上的頻次,逐個累加,確定元素排序後的位置下標,然後倒序遍歷原陣列,逐個找到元素位置構成收集後的資料表,倒序的目的是保證相同的數字保持原來相對位置不變,保證排序穩定性。
下面以示例來說明這個演算法:
假設a={8,2,3,4,3,6,6,3,9}, max=10。此時,將陣列a的所有資料都放到需要為0-9的桶中。如下圖:
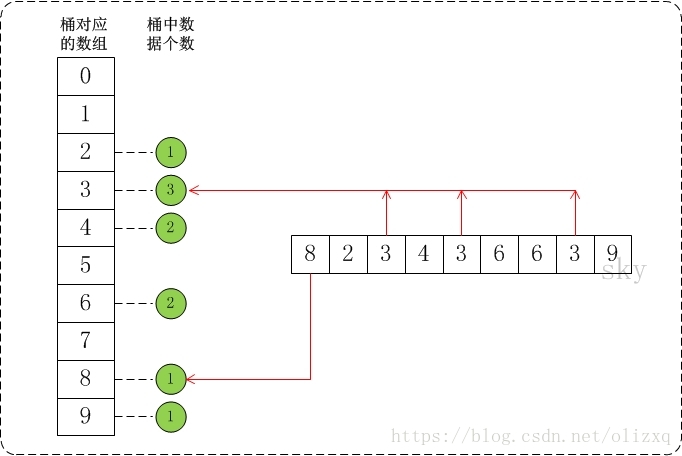
(3)演算法的步驟:
1.找出待排序的陣列中最大和最小的元素 2.統計陣列中每個值為i的元素出現的次數,存入陣列C的第i項 3.對所有的計數累加(從C中的第一個元素開始,每一項和前一項相加) 4.反向填充目標陣列:將每個元素i放在新陣列的第C(i)項,每放一個元素就將C(i)減去1
(4)時間複雜度
時間複雜度為O(n),且排序是穩定的。
(5)演算法實現(python)
"""
計數排序:
基本思想:
當資料表長度為n,已知資料表中資料的範圍有限,比如在範圍0−k之間,而k又比n小許多,這樣可以通過統計每一個範圍點上的資料頻次來實現計數排序。
演算法複雜度:O(n)
"""
def countSort(data):
data_order = [0] * len(data)
# 初始化計數陣列
count_arr = [0] * ((max(data) - min(data)) + 1)
# 統計i的次數
for i in range(len(data)):
count_arr[data[i] - min(data)] += 1
# 對所有的計數累加
for i in range(len(count_arr)-1):
count_arr[i+1] += count_arr[i]
# 逆向遍歷源陣列(保證穩定性),根據計數陣列中對應的值填充到先的陣列中
for i in range(len(data)-1, -1, -1):
data_order[count_arr[data[i] - min(data)]-1] = data[i]
count_arr[data[i] - min(data)] -= 1
return data_order
if __name__ == '__main__':
data = [20, 40, 30, 10, 60, 50]
print("before sort:", data)
# num_order = insertSort(num_list, num_len)
data_order = countSort(data)
print("after sort:", data_order)
執行結果:
before sort: [20, 40, 30, 10, 60, 50]
after sort: [10, 20, 30, 40, 50, 60]