最近在學群體優化演算法，做個學習筆記吧，本人蒟蒻，有不對的地方還情多多包涵。

1.粒子群演算法的理解。

        粒子群演算法是一種智慧優化演算法，模擬的是鳥內捕食行為。假設有一群鳥，在一個區域內覓食，這個區域內只有一個食物（最優解），但是每個鳥只知道自己距食物的距離，還有靠食物最近的鳥的距離（群體最優解），這樣，他們的覓食行為就收到三個方面的約束。

     （1）距離食物最近的鳥的位置，這樣所有的其他鳥都會向這隻鳥靠攏，即所有點都會向當前全域性最優解學習，靠攏。

     （2）光有全域性最優解，最後得到的解最優也只能是初始狀態的最優解，因此，每個鳥在靠近全域性最優解的過程中也會計算自己與食物之間的距離，有可能在某一時刻，自己的距離比全域性最優解還近，那麼更新全域性最優解，同時變更群體的學習方向。這就是個體最優解。

     （3）自身慣性。這是粒子繼承先前速度的能力。一個較大的慣性有助於全域性搜尋，而一個較小的慣性有助於區域性搜尋。因此，在平常設計中，我們將慣性w設定為動態慣性，確保前期全域性搜尋能力強，但在後期區域性搜尋能力強，從而提高演算法精度。

       所以，假設在一個D維的搜尋空間中，由n個粒子組成的種群X=（X1,X2....Xn），其中第i個粒子向量表示為Xi=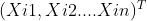,表示粒子在D維搜尋空間的位置，第i個粒子的速度為Vi=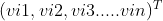,個體極值為Pi=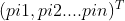,種群極值為Pg=;

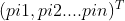則速度更新公式為

其中，w為慣性權重，k為迭代次數，Vid為粒子的速度；c1和c2為非負常數，也叫作加速度因子；r1和r2為【0,1】的分佈隨機數。

2.粒子群演算法的求解過程。

這裡我們以01揹包問題為例來模擬粒子群演算法。01揹包問題是著名的非線性尋優問題，適應度由價格和體積決定，而質量是總約束條件。整個演算法流程看程式碼吧，很清晰易懂的。

clear;
clc;
close all;

a=[95,4,60,32,23,72,80,62,65,46];        %物品體積
c=[55,10,47,5,4,50,8,61,85,87];          %物品價值
b=269;                                    %揹包重量

%初始化種群
Dim=10;           %維度
xSize=20;         %種群數
maxgen=30;        %迭代次數
c1=0.7;
c2=0.7;           %加速因子
w=0.8;            %定義慣性因子
%
A=repmat(a,xSize,1);      %將a擴充套件成30*10的矩陣
C=repmat(c,xSize,1);      %c擴充套件為30*10的矩陣
x=round(rand(xSize,Dim)); %隨機一個30*10的矩陣
v=rand(xSize,Dim)         %隨機一個30*10的速度矩陣
xbest=zeros(xSize,Dim);   %單個粒子的初始最佳位置
fxbest=zeros(xSize,1);    %xbext的適應度
gbest=zeros(1,Dim);       %全域性最優解
fgbest=0;                 %全域性最優解的適應度
%
%尋找粒子群最優位置和單個粒子
iter=0;
while iter<maxgen
    iter=iter+1;
    fx=sum((C.*x)');         %粒子適應度，即揹包內物品的價格
    sx=sum((A.*x)');         %限制函式，揹包內物品的體積
    for i=1:xSize
        if sx(i)>269
            fx(i)=0;         %超過體積，適應度為0
        end
    end
    for i=1:xSize
        if fxbest(i)<fx(i)   %當粒子適應度大於最佳適應度時，替代
            fxbest(i)=fx(i);
            xbest(i,:)=x(i,:);
        end
    end
    if fgbest<max(fxbest)
        [fgbest,g]=max(fxbest);
        gbest=xbest(g,:)     %當存在粒子的最佳適應度fxbext(i)大於種群最佳適應度fgbext(i)時，替代
    end
    for i=1:xSize
        if x(i,:)==gbest
            x(i,:)=round(rand(1,Dim));     %當某個粒子的位置為最佳位置時，重新賦值，以防止陷入區域性最優解
        end
    end
    R1=rand(xSize,Dim);
    R2=rand(xSize,Dim);
    v=v*w+c1*R1.*(xbest-x)+c2*R2.*(repmat(gbest,xSize,1)-x);%速度迭代公式產生新的速度
    x=x+v;          
    for i=1:xSize   %更新粒子群的位置
        for j=1:Dim
            if x(i,j)<0.5
                x(i,j)=0;
            else x(i,j)=1;   %粒子的位置只有（0,1）兩種狀態
            end
        end
    end
end

fgbest
sgbest=sum((a.*gbest)')
disp(gbest);
 

  最後的結果中，gbest的結果，0代表沒選，1代表選。