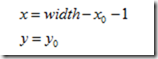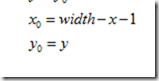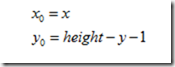影象的幾何變換是在不改變影象內容的前提下對影象畫素的進行空間幾何變換，主要包括了影象的平移變換、映象變換、縮放和旋轉等。本文首先介紹了影象幾何變換的一些基本概念，然後再OpenCV2下實現了影象的平移變換、映象變換、縮放以及旋轉，最後介紹幾何的組合變換（平移+縮放+旋轉）。

1.幾何變換的基本概念

1.1 座標對映關係

影象的幾何變換改變了畫素的空間位置，建立一種原影象畫素與變換後圖像畫素之間的對映關係，通過這種對映關係能夠實現下面兩種計算：

1. 原影象任意畫素計算該畫素在變換後圖像的座標位置
2. 變換後圖像的任意畫素在原影象的座標位置

對於第一種計算，只要給出原影象上的任意畫素座標，都能通過對應的對映關係獲得到該畫素在變換後圖像的座標位置。將這種輸入影象座標對映到輸出的過程稱為“向前對映

1. 對映不完全  輸入影象的畫素總數小於輸出影象，這樣輸出影象中的一些畫素找不到在原影象中的對映。 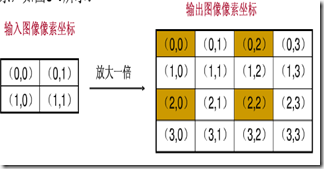  上圖只有(0,0),(0,2),(2,0),(2,2)四個座標根據對映關係在原影象中找到了相對應的畫素，其餘的12個座標沒有有效值。
2. 對映重疊  根據對映關係，輸入影象的多個畫素對映到輸出影象的同一個畫素上。 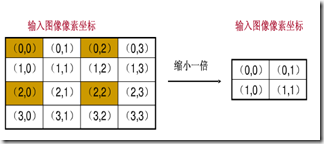  上圖左上角的四個畫素(0,0),(0,1),(1,0),(1,1)都會對映到輸出影象的(0,0)上，那麼(0,0)究竟取那個畫素值呢？

要解決上述兩個問題可以使用“向後對映”，使用輸出影象的座標反過來推算改座標對應於原影象中的座標位置。這樣，輸出影象的每個畫素都可以通過對映關係在原影象找到唯一對應的畫素，而不會出現對映不完全和對映重疊。所以，一般使用向後對映來處理影象的幾何變換。從上面也可以看出，向前對映之所以會出現問題，主要是由於影象畫素的總數發生了變化，也就是影象的大小改變了。在一些影象大小不會發生變化的變換中，向前對映還是很有效的。

1.2.插值演算法

對於數字影象而言，畫素的座標是離散型非負整數，但是在進行變換的過程中有可能產生浮點座標值。例如，原影象座標(9,9)在縮小一倍時會變成(4.5,4.5)，這顯然是一個無效的座標。插值演算法就是用來處理這些浮點座標的。常見的插值演算法有最鄰近插值法、雙線性插值法，二次立方插值法，三次立方插值法等。本文主要介紹最鄰近插值和雙線性插值，其他一些高階的插值演算法，以後再做研究。

1. 最鄰近插值  也被稱為零階插值法，最簡單插值演算法，當然效果也是最差的。它的思想相當簡單，就是四捨五入，浮點座標的畫素值等於距離該點最近的輸入影象的畫素值。 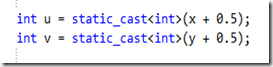  上面的程式碼可以求得(x,y)的最鄰近插值座標(u,v)。  最鄰近插值幾乎沒有多餘的運算，速度相當快。但是這種鄰近取值的方法是很粗糙的，會造成影象的馬賽克、鋸齒等現象。
2. 雙線性插值  它的插值效果比最鄰近插值要好很多，相應的計算速度也要慢上不少。雙線性插值的主要思想是計算出浮點座標畫素近似值。那麼要如何計算浮點座標的近似值呢。一個浮點座標必定會被四個整數座標所包圍，將這個四個整數座標的畫素值按照一定的比例混合就可以求出浮點座標的畫素值。混合比例為距離浮點座標的距離。  假設要求座標為(2.4,3)的畫素值P，該點在(2,3)和(3,3)之間，如下圖 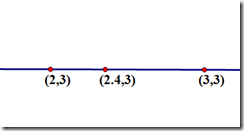 u和v分別是距離浮點座標最近兩個整數座標畫素在浮點座標畫素所佔的比例  P(2.4,3) = u * P(2,3) + v * P(3,3)，混合的比例是以距離為依據的，那麼u = 0.4,v = 0.6。  上面是隻在一條直線的插值，稱為線性插值。雙線性插值就是分別在X軸和Y軸做線性插值運算。  下面利用三次的線性插值進行雙線性插值運算 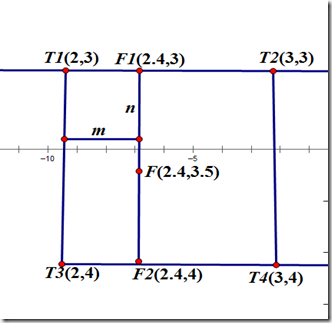  (2.4,3)的畫素值 F1 = m * T1 + (1 – m) * T2  (2.4,4)的畫素值 F2 = m * T3 + (1 – m ) * T4  (2.4,3.5)的畫素值 F = n * F1 + (1 – n) * F2  這樣就可以求得浮點座標(2.4,3.5)的畫素值了。  求浮點座標畫素F，設該浮點座標周圍的4個畫素值分別為T1，T2，T3，T4，並且浮點座標距離其左上角的橫座標的差為m，縱座標的差為n。  F1 = m * T1 + (1 – m) * T2  F2 = m * T3 +  (1 – m) *T4  F = n * F1 + (1 – n) * F2  上面就是雙線性插值的基本公式，可以看出，計算每個畫素畫素值需要進行6次浮點運算。而且，由於浮點座標有4個座標近似求得，如果這個四個座標的畫素值差別較大，插值後，會使得影象在顏色分界較為明顯的地方變得比較模糊。

2.影象平移

影象的平移變換就是將影象所有的畫素座標分別加上指定的水平偏移量和垂直偏移量。平移變換根據是否改變影象大小分為兩種   左邊平移影象的大小發生了，在保證影象平移的同時，也儲存了完整的影象資訊。右邊的平移影象大小沒有變化，故影象右下角的部分被截除了。

2.1平移變換原理

設dx為水平偏移量，dy為垂直偏移量，(x0,y0)為原影象座標，(x,y)為變換後圖像座標，則平移變換的座標對映為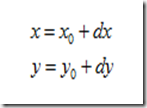 

這是向前對映，即將原影象的座標對映到變換後的影象上。  其逆變換為 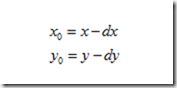,向後對映，即將變換後的影象座標對映到原影象上。在影象的幾何變換中，一般使用向後對映。

2.2 基於OpenCV的實現

影象的平移變換實現還是很簡單的，這裡不再贅述.

平移後圖像的大小不變 

void GeometricTrans::translateTransform(cv::Mat const& src, cv::Mat& dst, int dx, int dy)
{
    CV_Assert(src.depth() == CV_8U);

    const int rows = src.rows;
    const int cols = src.cols;

    dst.create(rows, cols, src.type());

    Vec3b *p;
    for (int i = 0; i < rows; i++)
    {
        p = dst.ptr<Vec3b>(i);
        for (int j = 0; j < cols; j++)
        {
            //平移後坐標對映到原影象
            int x = j - dx;
            int y = i - dy;

            //保證對映後的座標在原影象範圍內
            if (x >= 0 && y >= 0 && x < cols && y < rows)
                p[j] = src.ptr<Vec3b>(y)[x];
        }
    }
}

平移後圖像的大小變化 

void GeometricTrans::translateTransformSize(cv::Mat const& src, cv::Mat& dst, int dx, int dy)
{
    CV_Assert(src.depth() == CV_8U);

    const int rows = src.rows + abs(dy); //輸出影象的大小
    const int cols = src.cols + abs(dx);

    dst.create(rows, cols, src.type());
    Vec3b *p;
    for (int i = 0; i < rows; i++)
    {
        p = dst.ptr<Vec3b>(i);
        for (int j = 0; j < cols; j++)
        {
            int x = j - dx;
            int y = i - dy;

            if (x >= 0 && y >= 0 && x < src.cols && y < src.rows)
                p[j] = src.ptr<Vec3b>(y)[x];
        }
    }
}

ps：這裡影象變換的程式碼以三通道影象為例，單通道的於此類似，程式碼中沒有做處理。

3.影象的映象變換

影象的映象變換分為兩種：水平映象和垂直映象。水平映象以影象垂直中線為軸，將影象的畫素進行對換，也就是將影象的左半部和右半部對調。垂直映象則是以影象的水平中線為軸，將影象的上半部分和下班部分對調。效果如下： 

3.1變換原理

設影象的寬度為width，長度為height。(x,y)為變換後的座標，(x0,y0)為原影象的座標

1. 水平映象變換 向前對映  其逆變換為 向後對映
2. 垂直映象變換   其逆變換為 

3.2基於OpenCV的實現

水平映象的實現

void GeometricTrans::hMirrorTrans(const Mat &src, Mat &dst)
{
    CV_Assert(src.depth() == CV_8U);
    dst.create(src.rows, src.cols, src.type());

    int rows = src.rows;
    int cols = src.cols;

    switch (src.channels())
    {
    case 1:
        const uchar *origal;
        uchar *p;
        for (int i = 0; i < rows; i++){
            origal = src.ptr<uchar>(i);
            p = dst.ptr<uchar>(i);
            for (int j = 0; j < cols; j++){
                p[j] = origal[cols - 1 - j];
            }
        }
        break;
    case 3:
        const Vec3b *origal3;
        Vec3b *p3;
        for (int i = 0; i < rows; i++) {
            origal3 = src.ptr<Vec3b>(i);
            p3 = dst.ptr<Vec3b>(i);
            for(int j = 0; j < cols; j++){
                p3[j] = origal3[cols - 1 - j];
            }
        }
        break;
    default:
        break;
    }
    
}

分別對三通道影象和單通道影象做了處理，由於比較類似以後的程式碼只處理三通道影象，不再做特別說明。

在水平映象變換時，遍歷了整個影象，然後根據對映關係對每個畫素都做了處理。實際上，水平映象變換就是將影象座標的列換到右邊，右邊的列換到左邊，是可以以列為單位做變換的。同樣垂直映象變換也如此，可以以行為單位進行變換。

垂直映象變換 

void GeometricTrans::vMirrorTrans(const Mat &src, Mat &dst)
{
    CV_Assert(src.depth() == CV_8U);
    dst.create(src.rows, src.cols, src.type());

    int rows = src.rows;

    for (int i = 0; i < rows; i++)
        src.row(rows - i - 1).copyTo(dst.row(i));
}

src.row(rows - i - 1).copyTo(dst.row(i));

上面一行程式碼是變換的核心程式碼，從原影象中取出第i行，並將其複製到目標影象。

頂不住了啊，寫理論部分太痛苦了啊，明天繼續幾何變換的後續幾種：轉置、縮放、旋轉以及組合變換