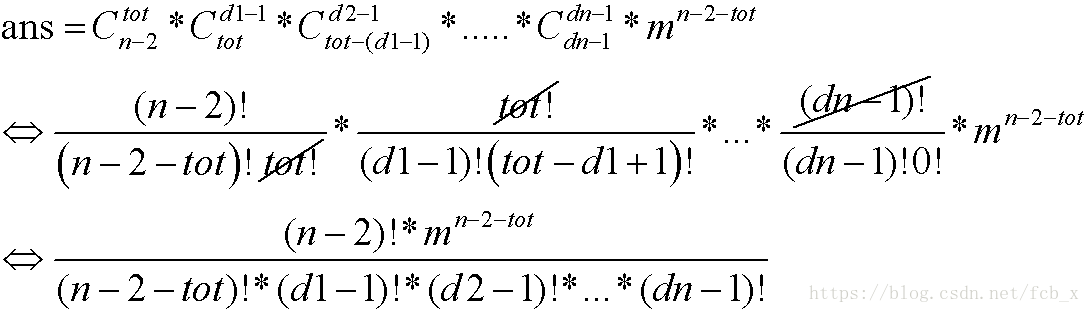wangyurzee有n個各不相同的節點，編號從1到n。wangyurzee想在它們之間連n-1條邊，從而使它們成為一棵樹。  可是wangyurzee發現方案數太多了，於是他又給出了m個限制條件，其中第i個限制條件限制了編號為u[i]的節點的度數不能為d[i]。 一個節點的度數，就是指和該節點相關聯的邊的條數。 這樣一來，方案數就減少了，問題也就變得容易了，現在請你告訴wangyurzee連邊的方案總數為多少。 答案請對1000000007取模。

發現給出的不可以的度數的點很少：

考慮容斥。

首先我們發現固定某個度數的答案是：

這個好理解就是在prufer序列中插入

然後注意同一個點的別算

然後就完了

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
typedef int INT;
#define int long long
inline void read(int &x){
	x=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')f=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9'){
		x=x*10+ch-'0';
		ch=getchar();
	}
	x*=f;
}
const int mod=1000000007;
const int N=1e6+100;
int fac[N];
int inv[N];
int Quick_Pow(int x,int k){
	int ret=1;
	while(k){
		if(k%2){
			ret=ret*x%mod;
		}
		x=x*x%mod;
		k/=2;
	}
	return ret;
}
int ans;
void Pre(){
	fac[0]=1;
	for(int i=1;i<N;++i){
		fac[i]=fac[i-1]*i%mod;
	}
	inv[N-1]=Quick_Pow(fac[N-1],mod-2);
	for(int i=N-2;i>=0;--i){
		inv[i]=inv[i+1]*(i+1)%mod;
	}
}
int n,m;
int Mx;
int u[20],d[20];
int vis[N];
INT main(){
	Pre();
	read(n);
	read(m);
	for(int i=0;i<m;++i){
		read(u[i]);
		read(d[i]);
	}
	Mx=(1<<m)-1;
	ans=Quick_Pow(n,n-2);
	for(int i=1;i<=Mx;++i){
//		memset(vis,0,sizeof(vis));
		int cnt=0;
		int tot=0;
		int ret=fac[n-2];
		int flag=0;
		for(int j=0;j<m;++j){
			if((1<<j)&i){
				if(vis[u[j]]){
					flag=1;
					break;
				}
				vis[u[j]]=1;
				cnt++;
				tot+=d[j]-1;
				ret=ret*inv[d[j]-1]%mod;
			}
		}
		if(!flag&&tot<=n-2) {
			ret=ret*inv[n-2-tot]%mod;
			ret=ret*Quick_Pow(n-cnt,n-2-tot)%mod;
			ans=((ans+ret*(cnt%2?-1:1))+mod)%mod;
		}
		for(int j=0;j<m;++j){
			if((1<<j)&i){
				vis[u[j]]=0;
			}
		}		
	}
	cout<<ans;
}