內容

1. 引數化表示式
2. 求平面法向量
3. 求點到平面的距離
4. 求直線與平面交點
5. 求三個平面斜交

1.  引數化表示式

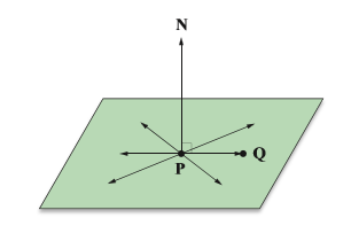
已知一個三維點 P 與法向量 N，設過點 P 且與 N 垂直的平面為點 Q 的合集，那麼 Q 滿足：

除此之外，平面方程還有一種常用的表達方式：

這裡的 A，B，C 其實就是法向量 N 的 x，y，z 分量，而

2. 求平面法向量

• 已知平面上兩條不共線的直線 ，，求法向量：

而根據叉積的定義，兩個向量的叉積所得的向量和這兩個向量垂直；

根據平面性質，垂直於平面的直線與平面上任何一條直線垂直；

因此，平面上兩不共線直線的叉積(兩平行直線的叉積為0)，就是該平面的法向量，方向遵循右手定則。 

• 已知平面方程 ，求法向量：

上述平面方程的三個係數所組成的向量 ，就是平面的一個法向量，證明如下：

設過平面上一點  的一個法向量為 ，該向量垂直於面上任意一條直線；

設  為平面上任意一點，則平面上的向量均可表示為：；

因為向量  與向量  垂直，所以其數量積為0，即：

整理得：

3. 求點到平面的距離

對於平面S1，有方程 ；

之前已經提到了 ，N為平面的法向量，P是平面S1上一點；

因為N是向量，P是一個點，可以先把  看做是向量N和向量OP的乘積(O為原點)，

以下描述和公式中的向量P皆指代向量OP。

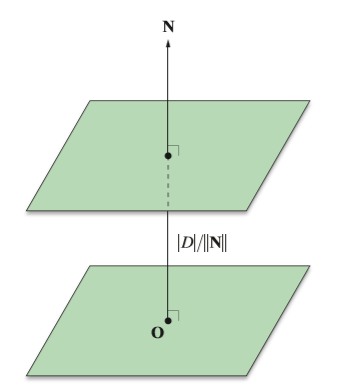
設過原點O與S1平行的平面為S0，因為：

其中為量N和向量P的夾角， 是向量P在法線向量N上投影的向量大小，也是S0和S1的之間的距離，則：

S0和S1的之間的距離為：  。

同理，設任意一點R，假設過點R且與平面S1，S0平行的平面為S2，則S0和S2之間的距離d2為：

若平面法向量N為單位向量，則點R到平面S1的距離為S0和S1之間的距離減去S0和S2之間的距離，即：

若d=0，則點R位於平面上；

若d>0，則點R位於平面法向量所指的一側，稱為平面的正向側

若d<0，則點R位於平面的負向側

4. 求直線與平面交點

求一條直線和一個平面的交點是3D圖形引擎中的普通計算，比如說在多邊形裁剪中被廣泛使用。

設過點S且與方向V平行的直線的表示式為：

設有一法向量為N且到原點的符號距離為D的平面，那麼則存在：

即存在P(t)直線過該平面的一點(當然也可能直線和平面平行了，沒有交點)

解上述關於P(t)的方程，即可獲得直線與平面的交點。將P(t)替換為，可得：

求解關於t的方程，可得：

將t的值代入直程即可求得交點。

如果 ，則直線與平面平行，且平面法向量N與直線方向向量V垂直，

此時，若，則直線位於平面上，否則無交點。

5. 求三個平面斜交

一個空間的區域通常表示成由一系列平面為邊界組成的凸面多面體的形式。該多面體的邊和頂點可以通過執行多次三個平面的求交運算得出。

• 求三個平面交於一點

設 ，，，為任意三個平面；

通過計算以下方程組的解可以得到同時位於這三個平面的點Q：

寫成矩陣形式：

其中，矩陣M的表示式如下：

假設矩陣M可逆，計算下式可得到三個平面的唯一交點Q：

如果矩陣M是奇異矩陣，即行列式為0：，則這三個平面不相交與一點；

當三個平面法向量位於同一平面時，會出現這種情況，下圖所示就是情況之一：

• 求兩個平面交於一條直線

設有兩個不平行的平面 和 相交時，其交於一條直線，如下圖所示：

交線的方向V與兩個平面的法向量都垂直，可表示為 ；

已知交線的方向，為了完整獲取表示式，還需要知道直線上的一點；

為此，構造經過原點且法向量為V的第三個平面 ，

可以確保三個平面交於一點，該點為平面  和  上的一點；

利用之前推倒的求三個平面的唯一交點的公式，可以得到交點Q：

則平面 和 交線的表示式為 。