單源最快求最短路-Dijsktra
最短路徑問題---Dijkstra演算法詳解
轉自:https://blog.csdn.net/qq_35644234/article/details/60870719
1、最短路徑問題介紹
問題解釋:
從圖中的某個頂點出發到達另外一個頂點的所經過的邊的權重和最小的一條路徑,稱為最短路徑
解決問題的演算法:
- 迪傑斯特拉演算法(Dijkstra演算法)
- 弗洛伊德演算法(Floyd演算法)
- SPFA演算法
這篇部落格,我們就對Dijkstra演算法來做一個詳細的介紹
2、Dijkstra演算法介紹
-
演算法特點:
迪科斯徹演算法使用了廣度優先搜尋解決賦權有向圖或者無向圖的單源最短路徑問題,演算法最終得到一個最短路徑樹。該演算法常用於路由演算法或者作為其他圖演算法的一個子模組。
-
演算法的思路
Dijkstra演算法採用的是一種貪心的策略,宣告一個數組dis來儲存源點到各個頂點的最短距離和一個儲存已經找到了最短路徑的頂點的集合:T,初始時,原點 s 的路徑權重被賦為 0 (dis[s] = 0)。若對於頂點 s 存在能直接到達的邊(s,m),則把dis[m]設為w(s, m),同時把所有其他(s不能直接到達的)頂點的路徑長度設為無窮大。初始時,集合T只有頂點s。
然後,從dis陣列選擇最小值,則該值就是源點s到該值對應的頂點的最短路徑,並且把該點加入到T中,OK,此時完成一個頂點,
然後,我們需要看看新加入的頂點是否可以到達其他頂點並且看看通過該頂點到達其他點的路徑長度是否比源點直接到達短,如果是,那麼就替換這些頂點在dis中的值。
然後,又從dis中找出最小值,重複上述動作,直到T中包含了圖的所有頂點。
3、Dijkstra演算法示例演示
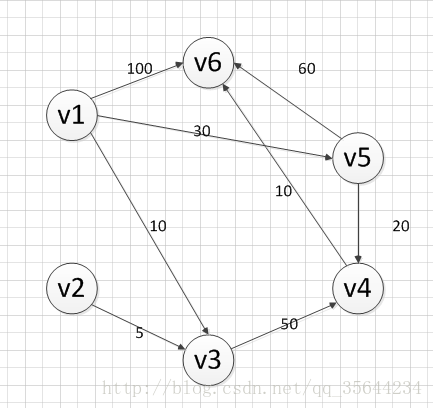
下面我求下圖,從頂點v1到其他各個頂點的最短路徑
首先第一步,我們先宣告一個dis陣列,該陣列初始化的值為:
我們的頂點集T的初始化為:T={v1}
既然是求 v1頂點到其餘各個頂點的最短路程,那就先找一個離 1 號頂點最近的頂點。通過陣列 dis 可知當前離v1頂點最近是 v3頂點。當選擇了 2 號頂點後,dis[2](下標從0開始)的值就已經從“估計值”變為了“確定值”,即 v1頂點到 v3頂點的最短路程就是當前 dis[2]值。將V3加入到T中。
為什麼呢?因為目前離 v1頂點最近的是 v3頂點,並且這個圖所有的邊都是正數,那麼肯定不可能通過第三個頂點中轉,使得 v1頂點到 v3頂點的路程進一步縮短了。因為 v1頂點到其它頂點的路程肯定沒有 v1到 v3頂點短.
OK,既然確定了一個頂點的最短路徑,下面我們就要根據這個新入的頂點V3會有出度,發現以v3 為弧尾的有: < v3,v4 >,那麼我們看看路徑:v1–v3–v4的長度是否比v1–v4短,其實這個已經是很明顯的了,因為dis[3]代表的就是v1–v4的長度為無窮大,而v1–v3–v4的長度為:10+50=60,所以更新dis[3]的值,得到如下結果:
因此 dis[3]要更新為 60。這個過程有個專業術語叫做“鬆弛”。即 v1頂點到 v4頂點的路程即 dis[3],通過 < v3,v4> 這條邊鬆弛成功。這便是 Dijkstra 演算法的主要思想:通過“邊”來鬆弛v1頂點到其餘各個頂點的路程。
然後,我們又從除dis[2]和dis[0]外的其他值中尋找最小值,發現dis[4]的值最小,通過之前是解釋的原理,可以知道v1到v5的最短距離就是dis[4]的值,然後,我們把v5加入到集合T中,然後,考慮v5的出度是否會影響我們的陣列dis的值,v5有兩條出度:< v5,v4>和 < v5,v6>,然後我們發現:v1–v5–v4的長度為:50,而dis[3]的值為60,所以我們要更新dis[3]的值.另外,v1-v5-v6的長度為:90,而dis[5]為100,所以我們需要更新dis[5]的值。更新後的dis陣列如下圖:
然後,繼續從dis中選擇未確定的頂點的值中選擇一個最小的值,發現dis[3]的值是最小的,所以把v4加入到集合T中,此時集合T={v1,v3,v5,v4},然後,考慮v4的出度是否會影響我們的陣列dis的值,v4有一條出度:< v4,v6>,然後我們發現:v1–v5–v4–v6的長度為:60,而dis[5]的值為90,所以我們要更新dis[5]的值,更新後的dis陣列如下圖:
然後,我們使用同樣原理,分別確定了v6和v2的最短路徑,最後dis的陣列的值如下:
因此,從圖中,我們可以發現v1-v2的值為:∞,代表沒有路徑從v1到達v2。所以我們得到的最後的結果為:
起點 終點 最短路徑 長度
v1 v2 無 ∞
v3 {v1,v3} 10
v4 {v1,v5,v4} 50
v5 {v1,v5} 30
v6 {v1,v5,v4,v6} 60
P4779 【模板】單源最短路徑(標準版)
Mode_Code:
#include<bits/stdc++.h>
using namespace std;
const int MaxN = 100010, MaxM = 500010;
struct Edg { int u, v, w, next; }edg[MaxM];
int head[MaxN], dis[MaxN], cnt;
bool vis[MaxN];
int n, m, s;
struct node
{
int dis;
int pos;
bool operator <(const node &x)const
{
return x.dis < dis;
}
};
std::priority_queue<node> q;
inline void dijkstra()
{
dis[s] = 0;
q.push(node{ 0, s });
while (!q.empty())
{
node tmp = q.top();
q.pop();
int x = tmp.pos, d = tmp.dis;
if (vis[x])
continue;
vis[x] = 1;
for (int i = head[x]; i; i = edg[i].next)
{
int y = edg[i].v;
if (dis[x] + edg[i].w<dis[y])
{
dis[y] = dis[x] + edg[i].w;
if (!vis[y])
{
q.push(node{ dis[y], y });
}
}
}
}
}
int main()
{
scanf("%d%d%d", &n, &m, &s);
for (int i = 1; i <= n; ++i)dis[i] = 0x7fffffff;
for (register int i = 1; i <=m; ++i)
{
register int u, v, d;
scanf("%d%d%d", &u, &v, &d);
edg[i] = Edg{ u,v,d,head[u] };
head[u] = i;
}
dijkstra();
for (int i = 1; i <= n; i++)
printf("%d ", dis[i]);
return 0;
}