一切起源於我在 caffe 的網站上看到的關於 SoftmaxLossLayer 的描述：

The softmax loss layer computes the multinomial logistic loss of the softmax of its inputs. It’s conceptually identical to a softmax layer followed by a multinomial logistic loss layer, but provides a more numerically stable gradient.

caffe 是當下一個很常用的 C++/CUDA 的 Deep Convolutional Neural Networks (CNNs) 的庫，由於清晰的程式碼結構和設計，並且速度也很快，所以不論是學術界還是工業界，要做一些擴充套件工作的時候經常會選用它。當然現在隨著 Deep Learning 的流行，相關的計算庫也繁榮起來，許多知名的庫大都有各自的特色，具體要選用哪一個的話還得看自己的需求而定。

不過今天我們主要是要圍繞上面引用的那一段話來閒聊一下。中心思想是：在數值計算（或者任何其他工程領域）裡，知道一個東西的基本演算法和寫出一個能在實際中工作得很好的程式之間還是有一段不小的距離的。有很多可能看似無關緊要的小細節小 trick，可能會對結果帶來很大的不同。當然這樣的現象其實也很合理：因為理論上的工作之所以漂亮正是因為抓住了事物的主要矛盾，忽略“無關”的細節進行了簡化和抽象，從而對比較“乾淨”的物件進行操作，在一系列的“assumption”下建立起理論體系。但是當要將理論應用到實踐中的時候，又得將這些之前被忽略掉了的細節全部加回去，得到一團亂糟糟，在一系列的“assumption”都不再嚴格滿足的條件下找出會出現哪些問題並通過一些所謂的“engineering trick”來讓原來的理論能“大致地”繼續有效，這些東西大概就主要是 Engineer 們所需要處理的事情了吧？這樣說來 Engineer 其實也相當不容易。這樣的話其實 Engineer 和 Scientist 的界線就又模糊了，就是工作在不同的抽象程度下的區別的樣子。

接下來閒話就不多說了，今天的主角 Softmax 其實並不一定要和 Deep Learning 有什麼關係，在 Logistic Regression 裡就可以看到它 (當然反過來說經典的 Deep Neural Networks 頂層其實本來也就是一個 Logistic Regression 分類器。)。具體來說，Softmax 函式  定義如下：

它在 Logistic Regression 裡其到的作用是講線性預測值轉化為類別概率：假設  是第  個類別的線性預測結果，帶入 Softmax 的結果其實就是先對每一個  取 exponential 變成非負，然後除以所有項之和進行歸一化，現在每個  就可以解釋成觀察到的資料  屬於類別  的概率，或者稱作似然 (Likelihood)。

然後 Logistic Regression 的目標函式是根據最大似然原則來建立的，假設資料  所對應的類別為 ，則根據我們剛才的計算最大似然就是要最大化  的值 (通常是使用 negative log-likelihood 而不是 likelihood，也就是說最小化  的值，這兩者結果在數學上是等價的。)。後面這個操作就是 caffe 文件裡說的 Multinomial Logistic Loss，具體寫出來是這個樣子：

而 Softmax-Loss 其實就是把兩者結合到一起，只要把  的定義展開即可

沒有任何 fancy 的東西。比如如果我們要寫一個 Logistic Regression 的 solver，那麼因為要處理的就是這個東西，比較自然地就可以將整個東西合在一起來考慮，或者甚至將  的定義直接一起帶進去然後對  和  進行求導來得到 Gradient Descent 的 update rule，例如我們之前介紹 Gradient Descent 的時候舉的兩類 Logistic Regression 的例子就是這樣做的。

反過來，如果是在設計 Deep Neural Networks 的庫，則可能會傾向於將兩者分開來看待：因為 Deep Learning 的模型都是一層一層疊起來的結構，一個計算庫的主要工作是提供各種各樣的 layer，然後讓使用者可以選擇通過不同的方式來對各種 layer 組合得到一個網路層級結構就可以了。比如使用者可能最終目的就是得到各個類別的概率似然值，這個時候就只需要一個 Softmax Layer，而不一定要進行 Multinomial Logistic Loss 操作；或者是使用者有通過其他什麼方式已經得到了某種概率似然值，然後要做最大似然估計，此時則只需要後面的 Multinomial Logistic Loss 而不需要前面的 Softmax 操作。因此提供兩個不同的 Layer 結構比只提供一個合在一起的 Softmax-Loss Layer 要靈活許多。從程式碼的角度來說也顯得更加模組化。但是這裡自然地就出現了一個問題：numerical stability。

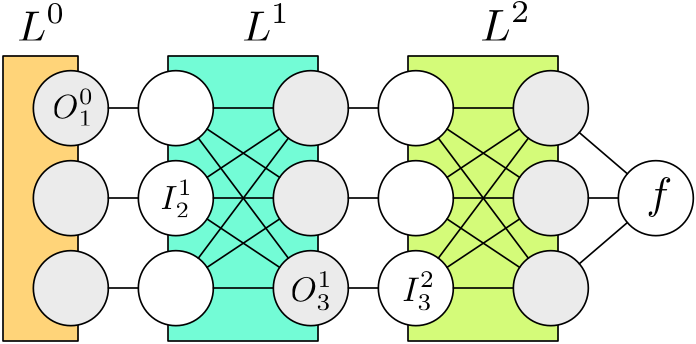
首先我們來看一下在神經網路中進行 gradient descent 的時候所謂的“Back Propagation”是什麼意思。例如圖中所示的一個 3 層神經網路，除了最開始的資料層  之外，每一層都有輸入節點和輸出節點，我們用  表示第一層的第二個輸入節點， 表示第一層的第三個輸出節點，每一層的輸入和輸出節點數量並不一定要一樣多，但是通常情況下某一層的輸入節點只是上一層的輸出節點的“複製”，比如 ，因為所有的計算操作是發生在每一層結構內部的。對於普通的神經網路，通常每一層進行的計算都是一個線性對映再經過一個 sigmoid 的非線性操作 ，例如：

後面是寫成向量/矩陣的形式，一般會顯得更簡潔。現在如果要對引數  進行求導以計算它的 gradient 來進行 gradient descent 一類的引數優化，利用微積分裡的 Chain Rule 可以得到如下的式子：

注意到紅色的部分是和第一層網路的內部結構相關的，只需要知道該層的區域性結構就可以進行計算，而藍色的部分，由於我們剛才說了輸出節點其實等於下一層的輸入節點，所以其實是 ，這個是可以在“上面”的第二層進行計算的，而不需要知道任何關於第一層的資訊。

因此整個網路的引數的 gradient 的計算方法是從頂層出發向後，在  層的時候，會拿到從  得到的  也就是 ，然後需要做兩個計算：首先是自己層內的引數的 gradient，比如如果是一個普通的全連通內積層，則會有引數  和 bias 引數 ，根據剛才的 Chain Rule 式子直接計算就可以了，如果  層沒有引數 (例如 Softmax 或者 Softmax-Loss 層就是沒有引數的。)，這一步可以省略；其次就是“向後傳遞”的步驟，同樣地，根據 Chain Rule 我們可以計算

計算出來的  將會作為  傳遞到  層，整個過程就叫做 Back Propagation，其實說白了就是 Chain Rule，只是涉及的符號有點多，容易搞混淆。

這裡順便可以跑題提一下在 Deep Learning 裡經常會聽到的 Vanishing Gradient 問題，因為 back propagation 是用 chain rule 將導數乘到一起，粗略地講，如果每一層的導數都“小於一”的話，在層數較多的情況下很容易到後面乘著乘著就接近零了。反過來如果每一層的導數都“大於一”的話，gradient 乘到最後又會出現 blow up 的問題。人們發明了很多技術來處理這些問題，不過那不是今天的話題。

搞清楚 Back Propagation 之後讓我們回到 Softmax-Loss 層，由於該層沒有引數，我們只需要計算向後傳遞的導數就可以了，此外由於該層是最頂層，所以不用使用 chain rule 就可以直接計算對於最終輸出（loss）的導數。回憶一下我們剛才的 notation，Softmax-Loss 層合在一起的時候我們用  來表示，它有兩個輸入，一個是 true label ，直接來自於最底部的資料層，並且我們不需要對資料層做任何的 gradient descent 引數更新，所以我們不需要像那個輸入進行 back propagation，但是另外一個輸入 則來自於下面的計算層，對於 Logistic Regression 或者普通的 DNNs 下面會是一個全連通的線性內積層，不過具體是什麼我們也不需要關心，只要把  計算出來丟給下面讓他們自己去算後面的就好了。根據普通的微積分知識，我們很容易算出：

其中  是 Softmax-Loss 的中間步驟 Softmax 在 Forward Pass 的計算結果，而

非常簡單對吧？接下來看如果是 Softmax 層和 Multinomial Logistic Loss 層分成兩層會是什麼樣的情況呢？繼續回憶剛才的記號：我們把 Softmax 層的輸出，也就是 Loss 層的輸入記為 ，因此我們首先要計算頂層的

然後我們把這個導數向下傳遞，現在到達 Softmax 層，在 apply chain rule 之前，首先計算層內的導數

如果用 Chain Rule 帶進去驗算一下的話：

和剛才的結果一樣的，看來我們求導沒有求錯。雖然最終結果是一樣的，但是我們可以看出，如果分成兩層計算的話，要多算好多步驟，除了計算量增大了一點，我們更關心的是數值上的穩定性。由於浮點數是有精度限制的，每多一次運算就會多累積一定的誤差，注意到分成兩步計算的時候我們需要計算 這個量，如果碰巧這次預測非常不準， 的值，也就是正確的類別所得到的概率非常小（接近零）的話，這裡會有 overflow 的危險。下面我們來實際試驗一下，首先定義好兩種不同的計算函式：

1. function softmax(z)
2. #z = z - maximum(z)
3. o = exp(z)
4. return o / sum(o)
5. end
6. function gradient_together(z, y)
7. o = softmax(z)
8. o[y] -= 1.0
9. return o
10. end
11. function gradient_separated(z, y)
12. o = softmax(z)
13. ∂o_∂z = diagm(o) - o*o'
14. ∂f_∂o = zeros(size(o))
15. ∂f_∂o[y] = -1.0 / o[y]
16. return ∂o_∂z * ∂f_∂o
17. end

然後由於 float (Float32) 比 double (Float64) 的精度要小很多，我們就以 double 的計算結果為近似的“正確值”，然後來比較兩種情況下通過 float 來計算得到的結果和正確值之差。繪圖程式碼如下：

1. using DataFrames
2. using Gadfly
3. M = 100
4. y = 1
5. zy = vec(10f0 .^ (-38:5:38)) # float range ~ [1.2*10^-38, 3.4*10^38]
6. zy = [-reverse(zy);zy]
7. srand(12345)
8. n_rep = 50
9. discrepancy_together = zeros(length(zy), n_rep)
10. discrepancy_separated = zeros(length(zy), n_rep)
11. for i = 1:n_rep
12. z = rand(Float32, M) # use float instead of double
13. discrepancy_together[:,i] = [begin
14. z[y] = x
15. true_grad = gradient_together(convert(Array{Float64},z), y)
16. got_grad = gradient_together(z, y)
17. abs(true_grad[y] - got_grad[y])
18. end for x in zy]
19. discrepancy_separated[:,i] = [begin
20. z[y] = x
21. true_grad = gradient_together(convert(Array{Float64},z), y)
22. got_grad = gradient_separated(z, y)
23. abs(true_grad[y] - got_grad[y])
24. end for x in zy]
25. end
26. df1 = DataFrame(x=zy, y=vec(mean(discrepancy_together,2)),
27. label="together")
28. df2 = DataFrame(x=zy, y=vec(mean(discrepancy_separated,2)),
29. label="separated")
30. df = vcat(df1, df2)
31. format_func(x) = @sprintf("%s10^%d", x<0?"-":"",int(log10(abs(x))))
32. the_plot = plot(df, x="x", y="y", color="label",
33. Geom.point, Geom.line, Geom.errorbar,
34. Guide.xticks(ticks=int(linspace(1, length(zy), 10))),
35. Scale.x_discrete(labels=format_func),
36. Guide.xlabel("z[y]"), Guide.ylabel("discrepancy"))

這裡我們做的事情是保持  的其他座標不變，而改變  也就是對應於真是 label 的那個座標的數值大小，我們剛才的推測是當  很接近零的時候會有 overflow 的危險，而 ，忽略掉 normalization 的話，正比於 ，所以我們需要把  那個座標設成絕對值很大的負數。在得到的圖中我們可以看到以整個數值範圍內的情況對比。 圖中橫座標是  的大小，縱座標是分別用兩種方法計算出來的結果和“真實值”之間的差距大小。

首先可以看到的是單層直接計算確實比分成兩層算要好一點，不過從縱座標上也可以看到兩者差距其實非常小。往左邊看的話，會發現黃色的點沒有了，那是因為結果得到了 NaN 了，比如  由於求一個絕對值非常大的負數的 exponential，導致下溢超出 float 可以表示的小數點精度範圍，直接變成 0 了，此時  就是 Inf，當要乘以  進行 cancel 的時候得到 ，對於浮點數這個操作會直接得到 NaN，也就是 Not a Number。反過來看藍線的話，好像有點奇怪的是越往左邊好像反而變得更加精確了，其實是因為我們的“真實值”也 underflow 了，因為 double 雖然比 float 精度高很多，但是也是有限制的。根據 Wikipedia，float 的精度範圍大致是 ，而 double 的精度範圍大致是 ，大了很多，但是我們不妨來看一下圖中的  這個座標點，注意到

所以 ，對於 float 來說已經下溢了，對於 double 來說還是可以表示的範圍，但是和 0 的差別也已經如此小，在圖上已經看不出區別來了。指數再移一格的話，，會直接導致 double 也 underflow，結果我們的“真實值”也會是零，所以“誤差”直接變成零了。

比較有趣的是往右邊的正數半軸看，發現到了  之後藍線和黃線都沒有了，說明他們都得到了 NaN，不過這裡是另一個問題：對一個比較大的數求 exponential 非常容易發生 overflow。還是用剛才的式子可以看到 ，已經超過了 float 可以表達的最大上限，所以會變成 Inf，然後在 normalize 的一步會出現 Inf/Inf 這樣的情況，於是就得到 NaN 了。

這個問題其實也是有解決辦法的，我們剛才貼的程式碼裡的 softmax 函式第一行有一行被註釋掉的程式碼，就是在求 exponential 之前將  的每一個元素減去  的最大值。這樣求 exponential 的時候會碰到的最大的數就是 0 了，不會發生 overflow 的問題，但是如果其他數原本是正常範圍，現在全部被減去了一個非常大的數，於是都變成了絕對值非常大的負數，所以全部都會發生 underflow，但是 underflow 的時候得到的是 0，這其實是非常 meaningful 的近似值，而且後續的計算也不會出現奇怪的 NaN。

當然，總不能在計算的時候平白無故地減去一個什麼數，但是在這個情況裡是可以這麼做的，因為最後的結果要做 normalization，很容易可以證明，這裡對  的所有元素同時減去一個任意數都是不會改變最終結果的——當然這只是形式上，或者說“數學上”，但是數值上我們已經看到了，會有很大的差別。

這就是本文的全部啦！如果想了解更多計算機浮點數值計算上會碰到的各種各樣的問題，也許在這本書裡會有更多的內容：《Numerical Computing with IEEE Floating Point Arithmetic: Including One Theorem, One Rule of Thumb, and One Hundred and One Exercises》。

最後，julia 允許 unicode 的變數名，於是可以寫各種帶數學符號的變數名了！而且 vim 的 julia 外掛有一個非常方便的功能就是能夠將 LaTeX 的符號命令補全成對應的 unicode 符號，比如輸入 \nabla 然後按 Tab，就會變成 ∇，非常方便。但是不得不念念碎一下的是很多地方還有待改進，比如現在載入一個像 Gadfly 繪相簿這種規模的 package 簡直就是要等到天荒地老，另外像這種沒有事先編譯的語言，哪裡寫錯了不到執行到那裡的時候都發現不了錯誤，可以想象我只是要寫一個小的繪圖 script 而已，寫完執行，等個 N 秒終於把繪相簿載入進來了然後碰到一個 typo，出錯了，修掉 typo 再執行，又是一輪等待，然後又碰到一個 typo……當然我寫程式碼比較粗心是我的問題，但是這種時候不得不就開始懷念編譯型語言啊。不過聽說現在正在開發的 0.4 版的一個重要內容就是靜態預編譯，這個功能實現之後各種庫應該都能做到瞬間載入。

另外還想吐槽的是，julia 裡輕量的 coroutine 和強大的巨集雖然是兩大賣點，但是卻也還是要掂量著點用啊。最主要的問題就是錯誤報告，之前嘗試過用 coroutine 來寫一個東西，由於沒有編譯期錯誤檢查，即使是很傻的程式碼錯誤也得等到執行期丟擲異常來排查，結果用了 coroutine 之後，經常都在 stack trace 裡找不到正確的出錯行號。還有巨集展開也是好像時不時會把錯誤彙報的行號搞亂掉。嘛，不過這些東西本來也就是雙刃劍了，就像 C++ 的 template 用來做模板超程式設計如果出錯的話也是會打印出幾千頁的編譯錯誤的。