20172304 藍墨雲實驗哈夫曼樹
阿新 • • 發佈:2018-12-12
20172304 藍墨雲實驗哈夫曼樹
實驗要求
- 設有字符集:S={a,b,c,d,e,f,g,h,i,j,k,l,m,n.o.p.q,r,s,t,u,v,w,x,y,z}。
給定一個包含26個英文字母的檔案,統計每個字元出現的概率,根據計算的概率構造一顆哈夫曼樹。
並完成對英文檔案的編碼和解碼。 - 要求:
- (1) 準備一個包含26個英文字母的英文檔案(可以不包含標點符號等),統計各個字元的概率
- (2) 構造哈夫曼樹
- (3) 對英文檔案進行編碼,輸出一個編碼後的檔案
- (4) 對編碼檔案進行解碼,輸出一個解碼後的檔案
- (5) 撰寫部落格記錄實驗的設計和實現過程,並將原始碼傳到碼雲
- (6) 把實驗結果截圖上傳到雲班課
哈夫曼編碼
- 哈夫曼編碼(Huffman Coding),又稱霍夫曼編碼,是一種編碼方式,哈夫曼編碼是可變字長編碼(VLC)的一種。Huffman於1952年提出一種編碼方法,該方法完全依據字元出現概率來構造異字頭的平均長度最短的碼字,有時稱之為最佳編碼,一般就叫做Huffman編碼(有時也稱為霍夫曼編碼)。
步驟:
- 對給定的n個權值{W1,W2,W3,...,Wi,...,Wn}構成n棵二叉樹的初始集合F= {T1,T2,T3,...,Ti,...,Tn},其中每棵二叉樹Ti中只有一個權值為Wi的根結點,它的左右子樹均為空。(為方便在計算機上實現算 法,一般還要求以Ti的權值Wi的升序排列。)
- 在F中選取兩棵根結點權值最小的樹作為新構造的二叉樹的左右子樹,新二叉樹的根結點的權值為其左右子樹的根結點的權值之和。
- 從F中刪除這兩棵樹,並把這棵新的二叉樹同樣以升序排列加入到集合F中。
- 重複上兩步的操作,直到集合F中只有一棵二叉樹為止,即為哈夫曼樹
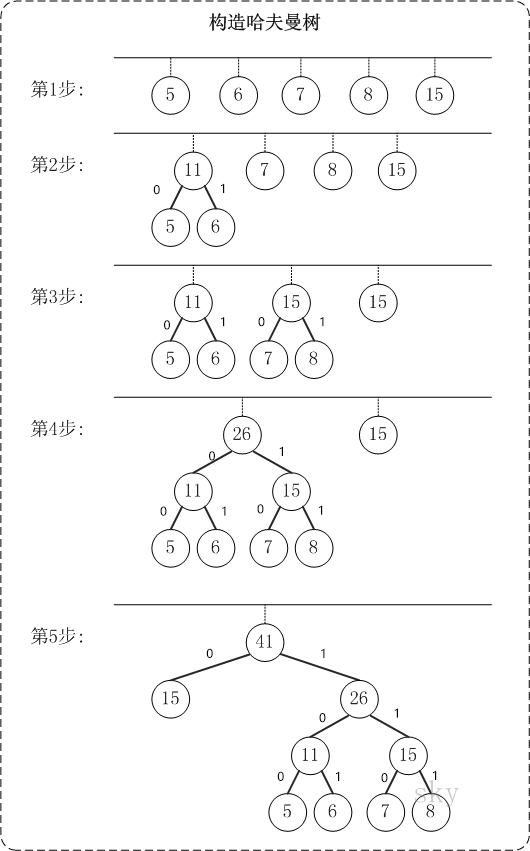
- 第1步:建立森林,森林包括5棵樹,這5棵樹的權值分別是5,6,7,8,15。
- 第2步:在森林中,選擇根結點權值最小的兩棵樹,即“樹5”和“樹6”來進行合併,將它們作為一顆新樹的左右子結點(誰左誰右無關緊要,這裡,我們選擇較小的作為左孩子),並且新樹的權值是左右子結點的權值之和。即,新樹的權值是11。然後,將"樹5"和"樹6"從森林中刪除,並將新的“樹11”新增到森林中。
- 第3步:在森林中,選擇根結點權值最小的兩棵樹即“樹7”和“樹8”來進行合併,得到的新樹的權值是15。然後,將"樹7"和"樹8"從森林中刪除,並將新的“樹15”新增到森林中。
- 第4步:在森林中,選擇根節點權值最小的兩棵樹(11和15)來進行合併。得到的新樹的權值是26。然後,將"樹11"和"樹15"從森林中刪除,並將新的樹(樹26)新增到森林中。
- 第5步:在森林中,選擇根節點權值最小的兩棵樹即“樹15”和“樹26”來進行合併,得到的新樹的權值是41。然後,將"樹15"和"樹26"從森林中刪除,並將新的“樹41”新增到森林中。
- 此時,森林中只有一棵樹(樹41)。這棵樹就是我們需要的哈夫曼樹!
- 各字元對應的編碼為:“15”->0, “26”->1, “5”->100, “6”->101, “7”->110, "8"->111
Java實現哈夫曼編碼
- 構造哈夫曼樹的結點類
- 在實現這個部分的時候,根據老師的PPT所示,需要新增元素資訊、權值、雙親、左孩子和右孩子,通過實現介面Comparable就利用權值進行比較,來確定是放在哈夫曼樹的左側還是右側,針對建立的問題可以仿照之前的建立二叉樹的結點差不多,給大家推薦一篇有關哈夫曼樹的部落格。在此基礎上,為了方便輸出它的0/1編碼,需要見一個code變數,用來確定每一個的編碼值。
public class HuffmanNode<T> implements Comparable<HuffmanNode<T>>{ private T letter; private double weight; private HuffmanNode lChild, rChild; private String code; public HuffmanNode(T letter, double weight){ this.letter = letter; this.weight = weight; code = ""; } public T getLetter() { return letter; } public double getWeight() { return weight; } public HuffmanNode getlChild() { return lChild; } public HuffmanNode getrChild() { return rChild; } public String getCode() { return code; } public void setLetter(T letter) { this.letter = letter; } public void setWeight(double weight) { this.weight = weight; } public void setlChild(HuffmanNode lChild) { this.lChild = lChild; } public void setrChild(HuffmanNode rChild) { this.rChild = rChild; } public void setCode(String code) { this.code = code; } @Override public String toString() { return "Huffman: " + letter + " 權值:" + weight + "編碼:" + code; } @Override public int compareTo(HuffmanNode<T> huffmanNode) { if(this.weight > huffmanNode.getWeight()) return -1; else return 1; } } - 構造哈夫曼樹
- 哈夫曼樹的構造,並不需要像建立二叉樹的那麼多的方法,滿足形成哈夫曼編碼的部分就好。分享的那篇部落格有相關的內容,我們只需要在此基礎上新增每次建立的的編碼值就可以,左側0右側1就可以。
- 建立樹,先將結點進行排序,利用結點類中實現的比較方法,分別將左孩子定義為列表中的倒數第二個,因為左側編碼為0,所以讓該結點的編碼為0;右孩子為列表中的倒數第一個,因為右側編碼為1,所以讓該結點的編碼為1,雙親結點根據所講內容為左右結點權重相加之和,把雙親結點加入列表中,然後刪除倒數兩個結點並新增雙親結點,再次進行迴圈,排序,不斷從列表中把倒數兩個結點刪除,直至跳出迴圈,此時列表中的結點只剩一個,該結點的左右部分包含了所有按照編碼進行新增的元素內容。
public HuffmanNode<T> createTree(List<HuffmanNode<T>> nodes) { while (nodes.size() > 1) { Collections.sort(nodes); HuffmanNode<T> left = nodes.get(nodes.size() - 2);//令其左孩子的編碼為0 left.setCode("0"); HuffmanNode<T> right = nodes.get(nodes.size() - 1);//令其右孩子的編碼為1 right.setCode("1"); HuffmanNode<T> parent = new HuffmanNode<T>(null, left.getWeight() + right.getWeight()); parent.setlChild(left); parent.setrChild(right); nodes.remove(left); nodes.remove(right); nodes.add(parent); } return nodes.get(0); }- 輸出編碼,利用哈夫曼樹的createTree方法來實現編碼內容,然後輸出每一個結點的編碼值,按照每個分支的0/1進行,左側0右側1進行。
public List<HuffmanNode<T>> breath(HuffmanNode<T> root) { List<HuffmanNode<T>> list = new ArrayList<HuffmanNode<T>>(); Queue<HuffmanNode<T>> queue = new LinkedList<>(); if (root != null) { queue.offer(root); root.getlChild().setCode(root.getCode() + "0"); root.getrChild().setCode(root.getCode() + "1"); } while (!queue.isEmpty()) { list.add(queue.peek()); HuffmanNode<T> node = queue.poll(); if (node.getlChild() != null) node.getlChild().setCode(node.getCode() + "0"); if (node.getrChild() != null) node.getrChild().setCode(node.getCode() + "1"); if (node.getlChild() != null) queue.offer(node.getlChild()); if (node.getrChild() != null) queue.offer(node.getrChild()); } return list; } - 編碼與解碼
- 編碼部分,需要按照讀取的內容進行新增每一個的編碼值,變數result即為編碼之後的內容,將這部分內容寫入一個檔案。
String result = ""; for(int f = 0; f < sum; f++){ for(int j = 0;j<letter.length;j++){ if(neirong.charAt(f) == letter[j].charAt(0)) result += code[j]; } }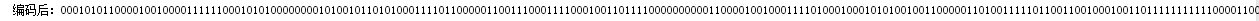
- 解碼部分,需要每次調出編碼內容的一個0/1,然後每讀出一位就要判斷一次是否有對應的編碼值,如果有就輸出,如果沒有就不斷往下讀取內容,並刪除讀出的內容避免重複讀取,直至將編碼的內容全部讀完解碼完成。利用兩個迴圈,外層迴圈進行每一次的新增一個編碼位,內層迴圈將新增一位的內容進行對比,符合就為編碼值,不符合就需要在新增一位。
for(int h = list4.size(); h > 0; h--){ string1 = string1 + list4.get(0); list4.remove(0); for(int i=0;i<code.length;i++){ if (string1.equals(code[i])) { string2 = string2+""+letter[i]; string1 = ""; } } }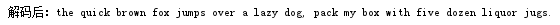
- 計算概率和重複次數
- 從檔案中進行讀取,並按照英文字母的種類進行記錄每一個字母的出現次數,這裡我添加了一個記錄空格、逗號和句號,便於編寫檔案內容。針對檔案中的內容總不能針對每一個位置都要迴圈確定一遍是否含有那個字母,利用我在實驗室嘗試過的程式碼,
Collections.frequency();來實現,裡面的兩個形式引數,按照第二個形式引數表現的內容,記錄其在第一個列表內的重複次數,這樣只需要將檔案內容一每個字元的形式存放在一個列表中就行,然後進行比對即可。總的字元數目就是每一個字母的重複次數。
for(int a = 0; a <= getFileLineCount(file); a++){ String tp = bufferedReader.readLine(); neirong += tp; for(int b = 0; b < tp.length(); b++){ list2.add(String.valueOf(tp.charAt(b))); } Esum[0] += Collections.frequency(list2, list1.get(0)); Esum[1] += Collections.frequency(list2, list1.get(1)); Esum[2] += Collections.frequency(list2, list1.get(2)); Esum[3] += Collections.frequency(list2, list1.get(3)); Esum[4] += Collections.frequency(list2, list1.get(4)); Esum[5] += Collections.frequency(list2, list1.get(5)); Esum[6] += Collections.frequency(list2, list1.get(6)); Esum[7] += Collections.frequency(list2, list1.get(7)); Esum[8] += Collections.frequency(list2, list1.get(8)); Esum[9] += Collections.frequency(list2, list1.get(9)); Esum[10] += Collections.frequency(list2, list1.get(10)); Esum[11] += Collections.frequency(list2, list1.get(11)); Esum[12] += Collections.frequency(list2, list1.get(12)); Esum[13] += Collections.frequency(list2, list1.get(13)); Esum[14] += Collections.frequency(list2, list1.get(14)); Esum[15] += Collections.frequency(list2, list1.get(15)); Esum[16] += Collections.frequency(list2, list1.get(16)); Esum[17] += Collections.frequency(list2, list1.get(17)); Esum[18] += Collections.frequency(list2, list1.get(18)); Esum[19] += Collections.frequency(list2, list1.get(19)); Esum[20] += Collections.frequency(list2, list1.get(20)); Esum[21] += Collections.frequency(list2, list1.get(21)); Esum[22] += Collections.frequency(list2, list1.get(22)); Esum[23] += Collections.frequency(list2, list1.get(23)); Esum[24] += Collections.frequency(list2, list1.get(24)); Esum[25] += Collections.frequency(list2, list1.get(25)); Esum[26] += Collections.frequency(list2, list1.get(26)); Esum[27] += Collections.frequency(list2, list1.get(27)); Esum[28] += Collections.frequency(list2, list1.get(28)); }

- 總個數
for(int c = 0; c < Esum.length; c++) sum += Esum[c]; System.out.println("總字母個數:" + sum);在此部分我用了一個可以確定檔案內容行數的方法,便於當檔案出現多行的時候的讀寫和編碼、解碼的相關操作。

- 從檔案中進行讀取,並按照英文字母的種類進行記錄每一個字母的出現次數,這裡我添加了一個記錄空格、逗號和句號,便於編寫檔案內容。針對檔案中的內容總不能針對每一個位置都要迴圈確定一遍是否含有那個字母,利用我在實驗室嘗試過的程式碼,
- 讀寫檔案
- 讀寫檔案的部分只需要呼叫File相關類進行編寫即可,我直接用了字元流直接將String型別的內容進行新增。
File file = new File("英文檔案.txt"); File file1 = new File("編碼檔案.txt"); File file2 = new File("解碼檔案.txt"); if (!file1.exists() && !file2.exists()) { file1.createNewFile(); file2.createNewFile(); } FileReader fileReader = new FileReader(file); BufferedReader bufferedReader = new BufferedReader(fileReader); FileWriter fileWriter1 = new FileWriter(file1); FileWriter fileWriter2 = new FileWriter(file2); fileWriter1.write(result); fileWriter2.write(string2); fileWriter1.close(); fileWriter2.close();
碼雲連結
感悟
- 哈夫曼編碼在剛開始的時候編得很混亂,在看過參考資料和同學的之後才理清思路,對於這種編碼形式,很大程度上的解決了資料壓縮的問題,便於儲存資料。