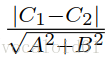時間限制：C/C++ 1秒，其他語言2秒 空間限制：C/C++ 1048576K，其他語言2097152K Special Judge, 64bit IO Format: %lld

題目描述

Eagle Jump公司正在開發一款新的遊戲。Hifumi Takimoto作為其中的員工，獲得了提前試玩的機會。現在她正在試圖通過一個迷宮。 這個迷宮有一些特點。為了方便描述，我們對這個迷宮建立平面直角座標系。迷宮中有兩條平行直線 L1:Ax+By+C1=0, L2:Ax+By+C2=0，還有 n 個圓 。角色在直線上、圓上、園內行走不消耗體力。在其他位置上由S點走到T點消耗的體力為S和T的歐幾里得距離。 Hifumi Takimoto想從 L1 出發，走到 L2 。請計算最少需要多少體力。

輸入描述:

第一行五個正整數 n,A,B,C1,C2 (1≤ n ≤ 1000, -10000 ≤ A,B,C1,C2 ≤ 10000)，其中 A,B 不同時為 0。
接下來 n 行每行三個整數 x,y,r(-10000 ≤ x,y ≤ 10000, 1≤ r ≤ 10000) 表示一個圓心為 (x,y)，半徑為 r 的圓。

輸出描述:

僅一行一個實數表示答案。與正確結果的絕對誤差或者相對誤差不超過 10-4 即算正確。

示例1

輸入

複製

2 0 1 0 -4
0 1 1
1 3 1

輸出

複製

0.236068

分析：

L1 到L2 之間連邊權值  

直線L與圓i 之間的權值 max( 0,dis(Oi,L)-Ri )

圓 i 與圓 j 之間的權值 max( 0,dis(Oi,Oj) -Ri-Rj )

求直線L1(0點)與直線L2(n+1點)之間的最短路

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e3+10;
const double eps=1e-4;
const double inf = 1e9+7;
int n;
int a,b,c1,c2;
bool vis[maxn];
double mp[maxn][maxn];
double dis[maxn];


struct circle
{
    int x,y;
    int r;
};
circle cir[maxn];
double dist(int i,int j)
{
    return sqrt((cir[i].x-cir[j].x)*(cir[i].x-cir[j].x)+(cir[i].y-cir[j].y)*(cir[i].y-cir[j].y));
}

double distLine(int c,int i)
{
    return fabs(a*cir[i].x + b*cir[i].y + c )/sqrt(a*a+b*b);
}

void spfa(int from,int to)
{
    memset(vis,0,sizeof vis);
    //memset(dis.inf,sizeof dis);
    for(int i=0;i<maxn;i++)
        dis[i]=inf;

    queue<int> q;
    q.push(from);
    vis[from]=true;
    dis[from]=0;
    while(!q.empty()){
        int cur=q.front();
        q.pop();
        vis[cur]=false;
        for(int i=0;i<=n+1;i++)
        {
            if(dis[i]>dis[cur]+mp[cur][i])
            {
                dis[i]=dis[cur]+mp[cur][i];
                if(!vis[i]){
                    vis[i]=true;
                    q.push(i);
                }
            }
        }
    }
}
int main()
{
    while(scanf("%d %d %d %d %d",&n,&a,&b,&c1,&c2)!=EOF){
        //printf("%d %d %d %d %d\n",n,a,b,c1,c2);
        for(int i=1;i<=n;i++){
            //printf("%d\n",i);
            scanf("%d%d%d",&cir[i].x,&cir[i].y,&cir[i].r);
        }

        double d=fabs(c1-c2)/sqrt(a*a+b*b);
        mp[0][n+1]=mp[n+1][0]=d;

        for(int i=1;i<=n;i++){
            d=distLine(c1,i)-cir[i].r;
            if(d<=eps)
                mp[0][i]=mp[i][0]=0;
            else
                mp[0][i]=mp[i][0]=d;

            d=distLine(c2,i)-cir[i].r;
            if(d<=eps)
                mp[n+1][i]=mp[i][n+1]=0;
            else
                mp[n+1][i]=mp[i][n+1]=d;

            for(int j=i+1;j<=n;j++){
                d=dist(i,j)-cir[i].r-cir[j].r;
                if(d<=eps)
                    mp[i][j]=mp[j][i]=0;
                else
                    mp[i][j]=mp[j][i]=d;
            }
        }
        spfa(0,n+1);
        printf("%.6lf\n",dis[n+1]);
    }
}