06-連結串列(上)如何實現LRU快取淘汰演算法
今天我們來聊聊“連結串列(Linked list)”這個資料結構。學習連結串列有什麼用呢?為了回答這個問題,我們先來討論一個經典的連結串列應用場景,那就是 LRU 快取淘汰演算法。
快取是一種提高資料讀取效能的技術,在硬體設計、軟體開發中都有著非常廣泛的應用,比如常見的 CPU 快取、資料庫快取、瀏覽器快取等等。
快取的大小有限,當快取被用滿時,哪些資料應該被清理出去,哪些資料應該被保留?這就需要快取淘汰策略來決定。常見的策略有三種:先進先出策略 FIFO(First In,First Out)、最少使用策略 LFU(Least Frequently Used)、最近最少使用策略 LRU(Least Recently Used)
這些策略你不用死記,我打個比方你很容易就明白了。假如說,你買了很多本技術書,但有一天你發現,這些書太多了,太佔書房空間了,你要做個大掃除,扔掉一些書籍。那這個時候,你會選擇扔掉哪些書呢?對應一下,你的選擇標準是不是和上面的三種策略神似呢?
好了,回到正題,我們今天的開篇問題就是:如何用連結串列來實現 LRU 快取淘汰策略呢? 帶著這個問題,我們開始今天的內容吧!
五花八門的連結串列結構 相比陣列,連結串列是一種稍微複雜一點的資料結構。對於初學者來說,掌握起來也要比陣列稍難一些。這兩個非常基礎、非常常用的資料結構,我們常常將會放到一塊兒來比較。所以我們先來看,這兩者有什麼區別。
我們先從底層的儲存結構上來看一看。
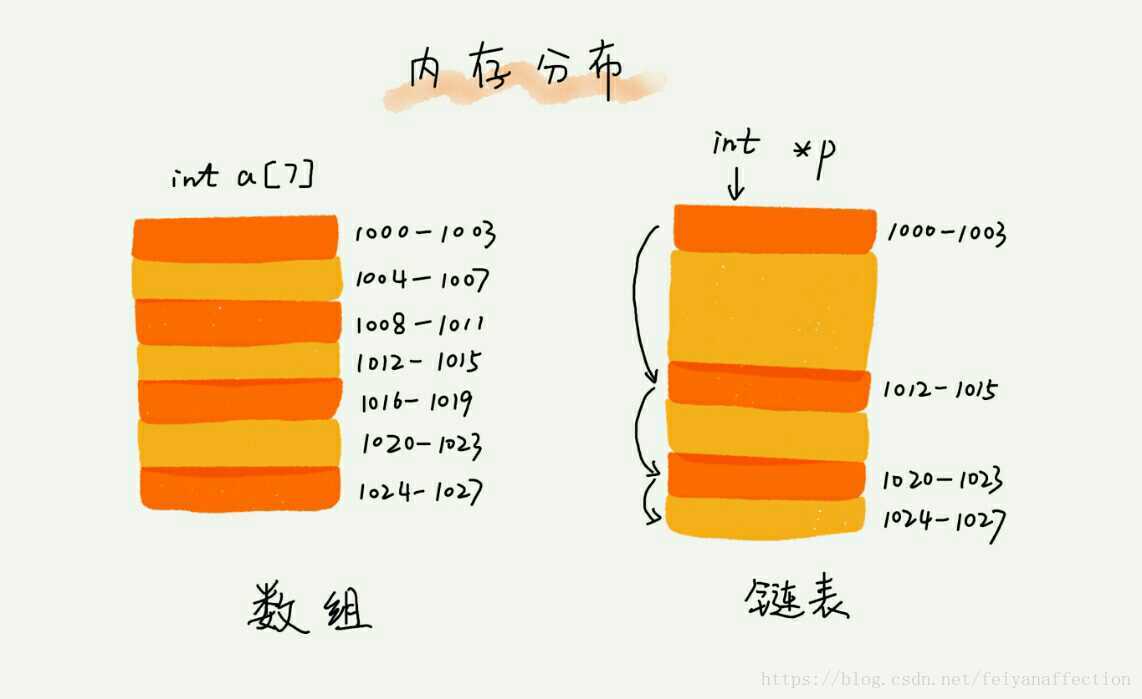
為了直觀地對比,我畫了一張圖。從圖中我們看到,陣列需要一塊連續的記憶體空間來儲存,對記憶體的要求比較高。如果我們申請一個 100MB 大小的陣列,當記憶體中沒有連續的、足夠大的儲存空間時,即便記憶體的剩餘總可用空間大於 100MB,仍然會申請失敗。
而連結串列恰恰相反,它並不需要一塊連續的記憶體空間,它通過“指標”將一組零散的記憶體塊串聯起來使用,所以如果我們申請的是 100MB 大小的連結串列,根本不會有問題。
連結串列結構五花八門,今天我重點給你介紹三種最常見的連結串列結構,它們分別是:單鏈表、雙向連結串列和迴圈連結串列。我們首先來看最簡單、最常用的單鏈表。
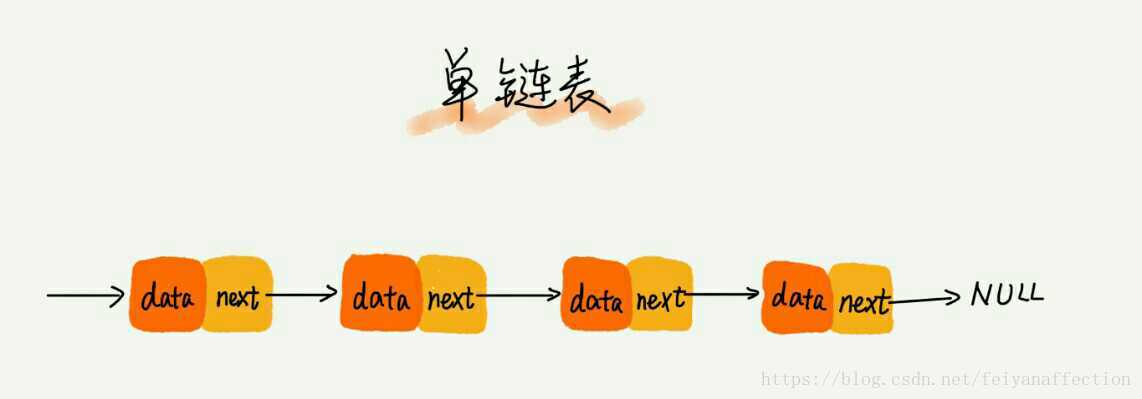
我們剛剛講到,連結串列通過指標將一組零散的記憶體塊串聯在一起。其中,我們把記憶體塊稱為連結串列的“結點”。為了將所有的結點串起來,每個連結串列的結點除了儲存資料之外,還需要記錄鏈上的下一個結點的地址。如圖所示,我們把這個記錄下個結點地址的指標叫作後繼指標 next。
從我畫的單鏈表圖中,你應該可以發現,其中有兩個結點是比較特殊的,它們分別是第一個結點和最後一個結點。我們習慣性地把第一個結點叫作頭結點,把最後一個結點叫作尾結點。其中,頭結點用來記錄連結串列的基地址。有了它,我們就可以遍歷得到整條連結串列。而尾結點特殊的地方是:指標不是指向下一個結點,而是指向一個空地址 NULL,表示這是連結串列上最後一個結點。
與陣列一樣,連結串列也支援資料的查詢、插入和刪除操作。
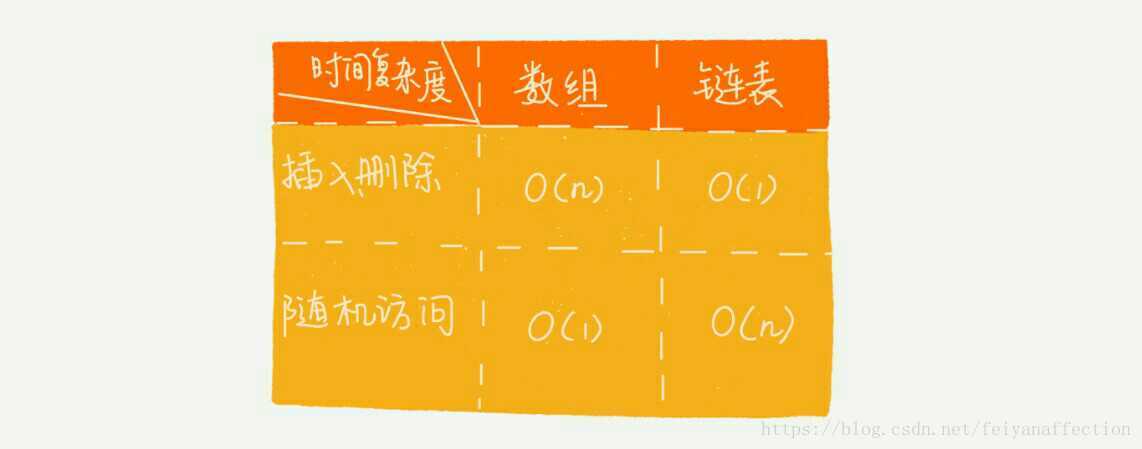
我們知道,在進行陣列的插入、刪除操作時,為了保持記憶體資料的連續性,需要做大量的資料搬移,所以時間複雜度是 O(n)。而在連結串列中插入或者刪除一個數據,我們並不需要為了保持記憶體的連續性而搬移結點,因為連結串列的儲存空間本身就不是連續的。所以,在連結串列中插入和刪除一個數據是非常快速的。
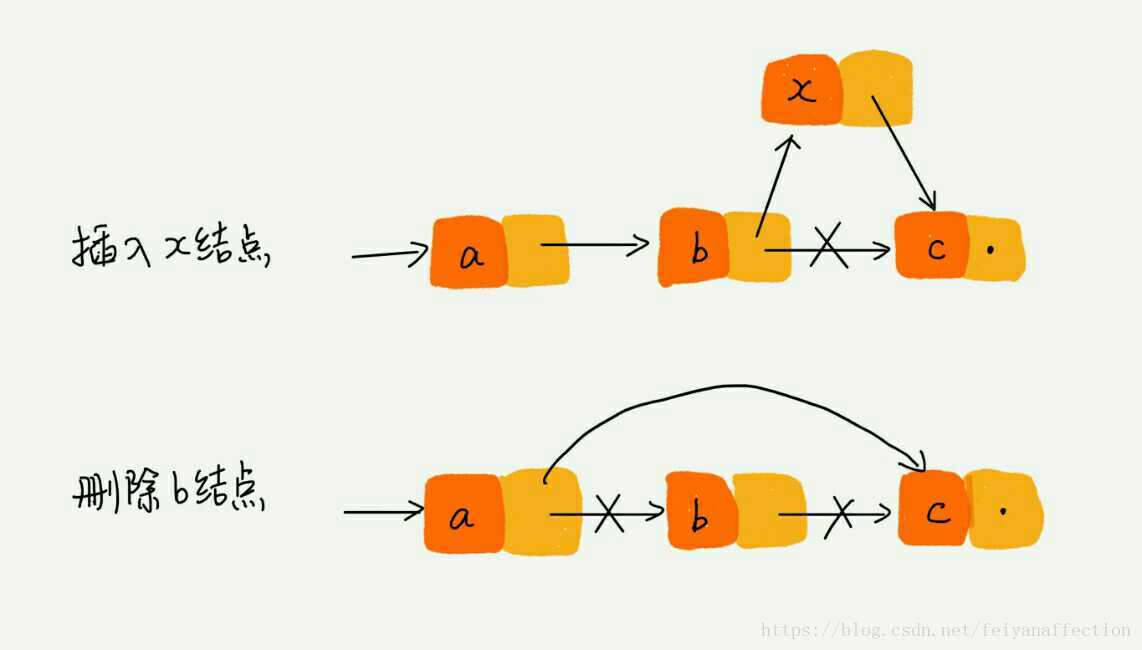
為了方便你理解,我畫了一張圖,從圖中我們可以看出,針對連結串列的插入和刪除操作,我們只需要考慮相鄰結點的指標改變,所以對應的時間複雜度是 O(1)。
但是,有利就有弊。連結串列要想隨機訪問第 k 個元素,就沒有陣列那麼高效了。因為連結串列中的資料並非連續儲存的,所以無法像陣列那樣,根據首地址和下標,通過定址公式就能直接計算出對應的記憶體地址,而是需要根據指標一個結點一個結點地依次遍歷,直到找到相應的結點。
你可以把連結串列想象成一個隊伍,隊伍中的每個人都只知道自己後面的人是誰,所以當我們希望知道排在第 k 位的人是誰的時候,我們就需要從第一個人開始,一個一個地往下數。所以,連結串列隨機訪問的效能沒有陣列好,需要 O(n) 的時間複雜度。
好了,單鏈表我們就簡單介紹完了,接著來看另外兩個複雜的升級版,迴圈連結串列和雙向連結串列。
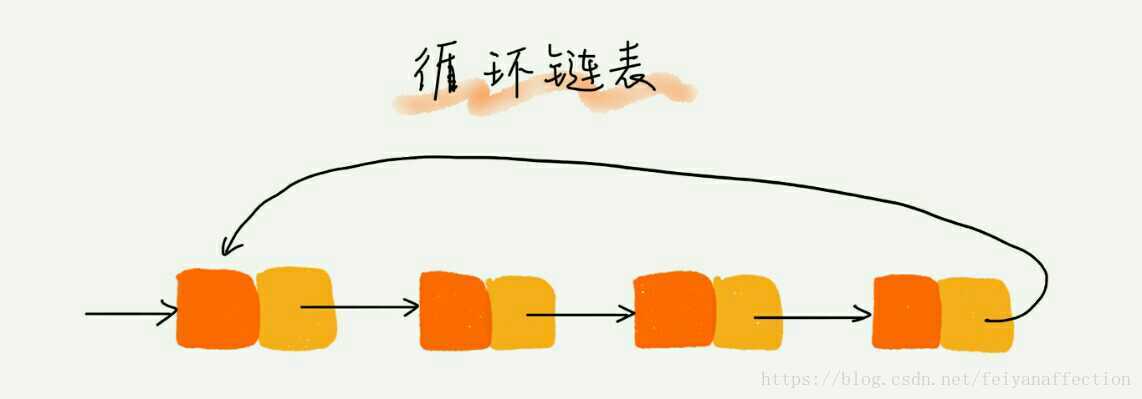
迴圈連結串列是一種特殊的單鏈表。實際上,迴圈連結串列也很簡單。它跟單鏈表唯一的區別就在尾結點。我們知道,單鏈表的尾結點指標指向空地址,表示這就是最後的結點了。而迴圈連結串列的尾結點指標是指向連結串列的頭結點。從我畫的迴圈連結串列圖中,你應該可以看出來,它像一個環一樣首尾相連,所以叫作“迴圈”連結串列。
和單鏈表相比,迴圈連結串列的優點是從鏈尾到鏈頭比較方便。當要處理的資料具有環型結構特點時,就特別適合採用迴圈連結串列。比如著名的約瑟夫問題。儘管用單鏈表也可以實現,但是用迴圈連結串列實現的話,程式碼就會簡潔很多。
單鏈表和迴圈連結串列是不是都不難?接下來我們再來看一個稍微複雜的,在實際的軟體開發中,也更加常用的連結串列結構:雙向連結串列。
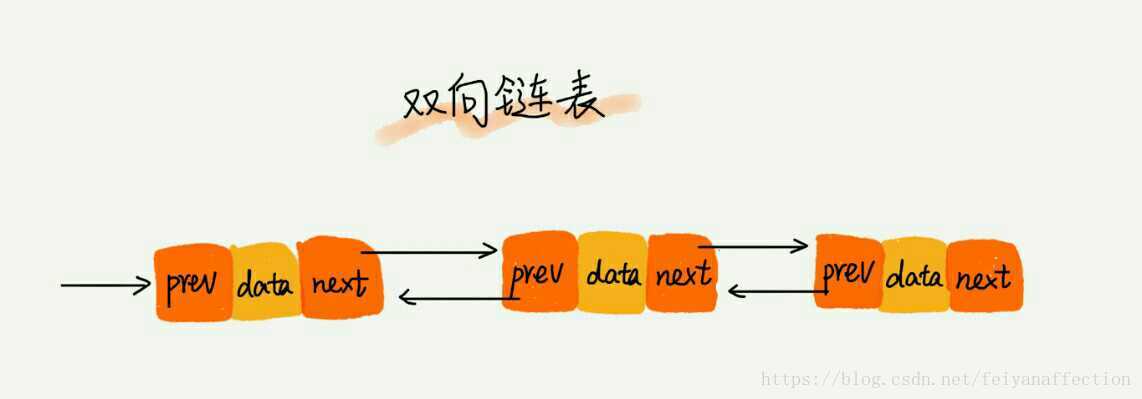
單向連結串列只有一個方向,結點只有一個後繼指標 next 指向後面的結點。而雙向連結串列,顧名思義,它支援兩個方向,每個結點不止有一個後繼指標 next 指向後面的結點,還有一個前驅指標 prev 指向前面的結點。
從我畫的圖中可以看出來,雙向連結串列需要額外的兩個空間來儲存後繼結點和前驅結點的地址。所以,如果儲存同樣多的資料,雙向連結串列要比單鏈表佔用更多的記憶體空間。雖然兩個指標比較浪費儲存空間,但可以支援雙向遍歷,這樣也帶來了雙向連結串列操作的靈活性。那相比單鏈表,雙向連結串列適合解決哪種問題呢?
從結構上來看,雙向連結串列可以支援 O(1) 時間複雜度的情況下找到前驅結點,正是這樣的特點,也使雙向連結串列在某些情況下的插入、刪除等操作都要比單鏈表簡單、高效。
你可能會說,我剛講到單鏈表的插入、刪除操作的時間複雜度已經是 O(1) 了,雙向連結串列還能再怎麼高效呢?彆著急,剛剛的分析比較偏理論,很多資料結構和演算法書籍中都會這麼講,但是這種說法實際上是不準確的,或者說是有先決條件的。我再來帶你分析一下連結串列的兩個操作。
我們先來看刪除操作。
在實際的軟體開發中,從連結串列中刪除一個數據無外乎這兩種情況:
刪除結點中“值等於某個給定值”的結點;
刪除給定指標指向的結點。
對於第一種情況,不管是單鏈表還是雙向連結串列,為了查詢到值等於給定值的結點,都需要從頭結點開始一個一個依次遍歷對比,直到找到值等於給定值的結點,然後再通過我前面講的指標操作將其刪除。
儘管單純的刪除操作時間複雜度是 O(1),但遍歷查詢的時間是主要的耗時點,對應的時間複雜度為 O(n)。根據時間複雜度分析中的加法法則,刪除值等於給定值的結點對應的連結串列操作的總時間複雜度為 O(n)。
對於第二種情況,我們已經找到了要刪除的結點,但是刪除某個結點 q 需要知道其前驅結點,而單鏈表並不支援直接獲取前驅結點,所以,為了找到前驅結點,我們還是要從頭結點開始遍歷連結串列,直到 p->next=q,說明 p 是 q 的前驅結點。
但是對於雙向連結串列來說,這種情況就比較有優勢了。因為雙向連結串列中的結點已經儲存了前驅結點的指標,不需要像單鏈表那樣遍歷。所以,針對第二種情況,單鏈表刪除操作需要 O(n) 的時間複雜度,而雙向連結串列只需要在 O(1) 的時間複雜度內就搞定了!
同理,如果我們希望在連結串列的某個指定結點前面插入一個結點,雙向連結串列比單鏈表有很大的優勢。雙向連結串列可以在 O(1) 時間複雜度搞定,而單向連結串列需要 O(n) 的時間複雜度。你可以參照我剛剛講過的刪除操作自己分析一下。
除了插入、刪除操作有優勢之外,對於一個有序連結串列,雙向連結串列的按值查詢的效率也要比單鏈表高一些。因為,我們可以記錄上次查詢的位置 p,每次查詢時,根據要查詢的值與 p 的大小關係,決定是往前還是往後查詢,所以平均只需要查詢一半的資料。
現在,你有沒有覺得雙向連結串列要比單鏈表更加高效呢?這就是為什麼在實際的軟體開發中,雙向連結串列儘管比較費記憶體,但還是比單鏈表的應用更加廣泛的原因。如果你熟悉 Java 語言,你肯定用過 LinkedHashMap 這個容器。如果你深入研究 LinkedHashMap 的實現原理,就會發現其中就用到了雙向連結串列這種資料結構。
實際上,這裡有一個更加重要的知識點需要你掌握,那就是用空間換時間的設計思想。當記憶體空間充足的時候,如果我們更加追求程式碼的執行速度,我們就可以選擇空間複雜度相對較高、但時間複雜度相對很低的演算法或者資料結構。相反,如果記憶體比較緊缺,比如程式碼跑在手機或者微控制器上,這個時候,就要反過來用時間換空間的設計思路。
還是開篇快取的例子。快取實際上就是利用了空間換時間的設計思想。如果我們把資料儲存在硬碟上,會比較節省記憶體,但每次查詢資料都要詢問一次硬碟,會比較慢。但如果我們通過快取技術,事先將資料載入在記憶體中,雖然會比較耗費記憶體空間,但是每次資料查詢的速度就大大提高了。
所以我總結一下,對於執行較慢的程式,可以通過消耗更多的記憶體(空間換時間)來進行優化;而消耗過多記憶體的程式,可以通過消耗更多的時間(時間換空間)來降低記憶體的消耗。你還能想到其他時間換空間或者空間換時間的例子嗎?
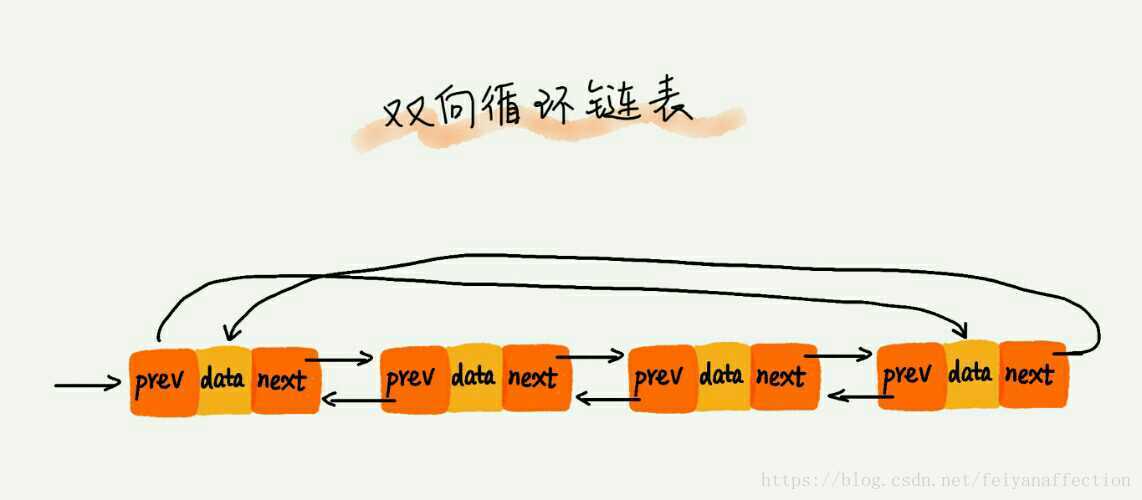
瞭解了迴圈連結串列和雙向連結串列,如果把這兩種連結串列整合在一起就是一個新的版本:雙向迴圈連結串列。我想不用我多講,你應該知道雙向迴圈連結串列長什麼樣子了吧?你可以自己試著在紙上畫一畫。
不過,陣列和連結串列的對比,並不能侷限於時間複雜度。而且,在實際的軟體開發中,不能僅僅利用複雜度分析就決定使用哪個資料結構來儲存資料。
陣列簡單易用,在實現上使用的是連續的記憶體空間,可以藉助 CPU 的快取機制,預讀陣列中的資料,所以訪問效率更高。而連結串列在記憶體中並不是連續儲存,所以對 CPU 快取不友好,沒辦法有效預讀。
陣列的缺點是大小固定,一經宣告就要佔用整塊連續記憶體空間。如果宣告的陣列過大,系統可能沒有足夠的連續記憶體空間分配給它,導致“記憶體不足(out of memory)”。如果宣告的陣列過小,則可能出現不夠用的情況。這時只能再申請一個更大的記憶體空間,把原陣列拷貝進去,非常費時。連結串列本身沒有大小的限制,天然地支援動態擴容,我覺得這也是它與陣列最大的區別。
你可能會說,我們 Java 中的 ArrayList 容器,也可以支援動態擴容啊?我們上一節課講過,當我們往支援動態擴容的陣列中插入一個數據時,如果陣列中沒有空閒空間了,就會申請一個更大的空間,將資料拷貝過去,而資料拷貝的操作是非常耗時的。
我舉一個稍微極端的例子。如果我們用 ArrayList 儲存了了 1GB 大小的資料,這個時候已經沒有空閒空間了,當我們再插入資料的時候,ArrayList 會申請一個 1.5GB 大小的儲存空間,並且把原來那 1GB 的資料拷貝到新申請的空間上。聽起來是不是就很耗時?
除此之外,如果你的程式碼對記憶體的使用非常苛刻,那陣列就更適合你。因為連結串列中的每個結點都需要消耗額外的儲存空間去儲存一份指向下一個結點的指標,所以記憶體消耗會翻倍。而且,對連結串列進行頻繁的插入、刪除操作,還會導致頻繁的記憶體申請和釋放,容易造成記憶體碎片,如果是 Java 語言,就有可能會導致頻繁的 GC(Garbage Collection,垃圾回收)。
所以,在我們實際的開發中,針對不同型別的專案,要根據具體情況,權衡究竟是選擇陣列還是連結串列。
解答開篇 好了,關於連結串列的知識我們就講完了。我們現在回過頭來看下開篇留給你的思考題。如何基於連結串列實現 LRU 快取淘汰演算法?
我的思路是這樣的:我們維護一個有序單鏈表,越靠近連結串列尾部的結點是越早之前訪問的。當有一個新的資料被訪問時,我們從連結串列頭開始順序遍歷連結串列。
-
如果此資料之前已經被快取在連結串列中了,我們遍歷得到這個資料對應的結點,並將其從原來的位置刪除,然後再插入到連結串列的頭部。
-
如果此資料沒有在快取連結串列中,又可以分為兩種情況:
如果此時快取未滿,則將此結點直接插入到連結串列的頭部;
如果此時快取已滿,則連結串列尾結點刪除,將新的資料結點插入連結串列的頭部。
這樣我們就用連結串列實現了一個 LRU 快取,是不是很簡單?
現在我們來看下 m 快取訪問的時間複雜度是多少。因為不管快取有沒有滿,我們都需要遍歷一遍連結串列,所以這種基於連結串列的實現思路,快取訪問的時間複雜度為 O(n)。
實際上,我們可以繼續優化這個實現思路,比如引入散列表(Hash table)來記錄每個資料的位置,將快取訪問的時間複雜度降到 O(1)。因為要涉及我們還沒有講到的資料結構,所以這個優化方案,我現在就不詳細說了,等講到散列表的時候,我會再拿出來講。
除了基於連結串列的實現思路,實際上還可以用陣列來實現 LRU 快取淘汰策略。如何利用陣列實現 LRU 快取淘汰策略呢?我把這個問題留給你思考。
內容小結 今天我們講了一種跟陣列“相反”的資料結構,連結串列。它跟陣列一樣,也是非常基礎、非常常用的資料結構。不過連結串列要比陣列稍微複雜,從普通的單鏈表衍生出來好幾種連結串列結構,比如雙向連結串列、迴圈連結串列、雙向迴圈連結串列。
和陣列相比,連結串列更適合插入、刪除操作頻繁的場景,查詢的時間複雜度較高。不過,在具體軟體開發中,要對陣列和連結串列的各種效能進行對比,綜合來選擇使用兩者中的哪一個。
課後思考?
如何判斷一個字串是否是迴文字串的問題,我想你應該聽過,我們今天的思題目就是基於這個問題的改造版本。如果字串是通過單鏈表來儲存的,那該如何來判斷是是一個迴文串呢?你有什麼好的解決思路呢?相應的時間空間複雜度又是多少呢?
應用:
1.如何分別用連結串列和陣列實現LRU緩衝淘汰策略? 1)什麼是快取? 快取是一種提高資料讀取效能的技術,在硬體設計、軟體開發中都有著非廣泛的應用,比如常見的CPU快取、資料庫快取、瀏覽器快取等等。 2)為什麼使用快取?即快取的特點 快取的大小是有限的,當快取被用滿時,哪些資料應該被清理出去,哪些資料應該被保留?就需要用到快取淘汰策略。 3)什麼是快取淘汰策略? 指的是當快取被用滿時清理資料的優先順序。 4)有哪些快取淘汰策略? 常見的3種包括先進先出策略FIFO(First In,First Out)、最少使用策略LFU(Least Frenquently Used)、最近最少使用策略LRU(Least Recently Used)。 5)連結串列實現LRU快取淘汰策略 當訪問的資料沒有儲存在快取的連結串列中時,直接將資料插入連結串列表頭,時間複雜度為O(1);當訪問的資料存在於儲存的連結串列中時,將該資料對應的節點,插入到連結串列表頭,時間複雜度為O(n)。如果快取被佔滿,則從連結串列尾部的資料開始清理,時間複雜度為O(1)。 6)陣列實現LRU快取淘汰策略 方式一:首位置儲存最新訪問資料,末尾位置優先清理 當訪問的資料未存在於快取的陣列中時,直接將資料插入陣列第一個元素位置,此時陣列所有元素需要向後移動1個位置,時間複雜度為O(n);當訪問的資料存在於快取的陣列中時,查詢到資料並將其插入陣列的第一個位置,此時亦需移動陣列元素,時間複雜度為O(n)。快取用滿時,則清理掉末尾的資料,時間複雜度為O(1)。 方式二:首位置優先清理,末尾位置儲存最新訪問資料 當訪問的資料未存在於快取的陣列中時,直接將資料新增進陣列作為當前最有一個元素時間複雜度為O(1);當訪問的資料存在於快取的陣列中時,查詢到資料並將其插入當前陣列最後一個元素的位置,此時亦需移動陣列元素,時間複雜度為O(n)。快取用滿時,則清理掉陣列首位置的元素,且剩餘陣列元素需整體前移一位,時間複雜度為O(n)。(優化:清理的時候可以考慮一次性清理一定數量,從而降低清理次數,提高效能。) 2.如何通過單鏈表實現“判斷某個字串是否為水仙花字串”?(比如 上海自來水來自海上) 1)前提:字串以單個字元的形式儲存在單鏈表中。 2)遍歷連結串列,判斷字元個數是否為奇數,若為偶數,則不是。 3)將連結串列中的字元倒序儲存一份在另一個連結串列中。 4)同步遍歷2個連結串列,比較對應的字元是否相等,若相等,則是水仙花字串,否則,不是。
二、設計思想
時空替換思想:“用空間換時間” 與 “用時間換空間” 當記憶體空間充足的時候,如果我們更加追求程式碼的執行速度,我們就可以選擇空間複雜度相對較高,時間複雜度小相對較低的演算法和資料結構,快取就是空間換時間的例子。如果記憶體比較緊缺,比如程式碼跑在手機或者微控制器上,這時,就要反過來用時間換空間的思路
1.快進慢進法[兩組指標,從頭開始,a組一次進一,b組一次進二,b組到終點時,a組位置即為連結串列中間結點,迴圈次數為連結串列除去中間結點後前後兩組的長度] 求得單向連結串列“中間”節點。並計算遍歷次數,經過驗證,遍歷次數為‘’半連結串列‘’長度 2.從中間結點開始,以動態步長[每第i次步長是半連結串列長度-i+1]遍歷連結串列,同時,從頭節點開始,以1步長遍歷。比較兩組對應元素是否相同,相同繼續,不同退出,返回不是迴文字串的結論。 3.返回是迴文字串的結論,退出. 空間複雜度O(n). 不用連續記憶體,可以磁碟操作 時間複雜度度O(n). 主要費時操作遍歷
3.單向遍歷,獲得對應的線性表Arr,求線性表長度為L 4.運用線性表可以任意訪問的性質,遍歷Arr,令下標i從0。比較Arr[i]和Arr[L-i]是否相等 相等繼續,不等報告不是迴文字串結論,退出 3.報告是迴文字串結論,結束。 空間複雜度O(n) 時間複雜度O(n) 看起來一樣,這個就需要字串不太大,有足夠的連續記憶體可以分配,而且,預先不知道連結串列多長,可能還會遇到擴容問題。