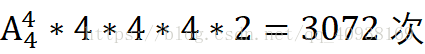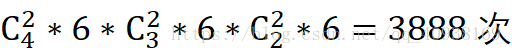【程式設計心得系列*24點】

寫在前面：程式設計心得系列不談具體問題的程式碼，只談解決思路。

這是一個關於二十四點的軟體。屬於典型的先有目的再有初衷的軟體。

在此之前我倒是寫過一個解數獨的軟體。但那個的核心程式碼部分畢竟是抄襲的。這次是覺得對自己更有信心，也是想就此考驗一下最近的程式設計學習，因而，挑選了看上去不是而很有難度的24點作為突破點，以此來在實踐中進一步學習。

二十四點問題

輸入：四個數字

操作：以不同順序和不同符號不斷匹配，直到算得24點並輸出。

輸出：是否可以算得24點，若可以，輸出方法。

很自然的我想到如下方法，書寫一個等式：

A？B？C?D=24  （？對應的是不同運算子）

不停的替換ABCD和運算子，佐之以不同括號位置，直到算出二十點為止。

最開始困惑我的主要方面在於——運算優先順序。如果加減乘除還有括號放在了一個公式中，那麼排序優先級別就是我首先應該做的事情了。左一個括號，右一個括號，需要討論的括號分類非常多，而每種分類又只對應了很少量的類別。這種分類價值顯得很低，用起來讓人很不愉快。而且，要實現一個運算優先順序的演算法，也不是一個簡單的操作。

否定了自己思路的我查看了網上諸多解算24點的演算法。這些演算法質量層次不齊，其中大部分就是不斷進行分類，多者甚至可以分出十多個類別。

實在不想費盡心思去學習別人那低劣的演算法的我，終止了對此問題的探索。

方法一

後來我和朋友D君一起散步。說明我的困惑（帶著吐槽的目的）。他說，你思考的方法不對，他說，我給你四個數字，你算一下24點。

他給的四個數字是：

4 3 4 4

我說，這有何難啊。3加4得到7, 7乘以4得到28，28減去4等於24。

接著D君說，你算的時候，要進行復雜的分類麼？

聰明，我暗中誇獎他。下邊是他提供的思路的歸納。

解決24點演算法之——基數擴充法。

說明：在四個數字中挑選一個數，將之當成基數，不斷對其加減乘除其他數來修改他，直到將之修改為24點。

所以，以迴圈圖的方式表示此過程，如下圖。

For（在四個數字中挑一個數字A）

For（挑選計算符號Z1）

   For（在剩下的三個數字中再挑一個數字B）計算result1=JiSuan（A,Z1,B）；

     For（挑選一個計算符號Z2）

  For（在剩下的兩個數字中再挑一個數字C）計算result2=JiSuan（result1,Z2,C）；

   For（挑選一個計算符號Z3）

    For（選出最後的數字D）{計算result3=JiSuan（result1,Z2,C）；if（result3==24）輸出；}

基數擴充法雖然好，但無法包含所有可能。還存在一種可能。例如1 2 3 5，那麼解決這個問題的最好方式就是（1+2）*（3+5）。顯然的，這兒要進行兩個基數擴充。所以，方法與上邊一樣。（請讀者自己思考，並像上邊那樣寫出流程圖）

這個演算法解決該問題需要計算：

這個數字可以說是相當的小，計算機完全可以在1ms內完成這個操作。

方法二

第一種方法已經很好。但後來，與另一個朋友小Z聊天，他看了我的演算法，搖頭說道：你這個方法不好，不具有通用性。

小Z問我：

為什麼一定要從一個數字開始到算出24為止？為什麼不反過來？能否考慮一下分治法（一種迴圈迭代的演算法）？

高明，我一拍手，整理出了思路。

問題：將N個數字進行加減乘除得到24。

步驟：1.將兩個數字合併為一個新的數字。（共存在相加，相乘，除以，減去，被除，被減6種可能）

2.將N-1個數字加減乘除得到24。

#當N=2，可以直接判斷

那麼，這樣解決這個問題的總的執行次數就是：

可以看到，比第一種演算法略多一些。但對計算機而言，這個數字仍舊相當小。但這段演算法可以解決N個數算24點的問題，更具有通用性。

演算法如下：

解決24點演算法之——分治法。

Get24（長度為N陣列）

{

If（N==2）就反覆套加減乘除，判斷是否可以為24點，若可，則輸出。

If（N!=2）就從中選出兩個數字，合併為為一個新的數字，並倒入一個新的陣列，N-1陣列，並對之呼叫Get24(長度為N-1的陣列)；

}

最後是文末的一點總結。不得不感慨，一個好的演算法真的是思維的火花。第一：開開腦洞，進行類比，換種方向思考，想想自己學習的資料結構知識。第二：對24點問題，還有其他問題，都要先想清楚思路，繪製好流程圖然後再下手。第三：絕知此事要躬行。

望各位程式設計道路上的學習者不斷總結，不斷奮進。

2018.9.6