前言

本篇繼續收集一些常見的python筆試題，以基礎知識為主，遞迴是面試最喜歡考的一個問題，不管是做開發還是測試，都無法避免考遞迴。本篇結合實際案例，講下幾種關於遞迴的場景。

計算n的階乘

計算n!,例如n=3(計算321=6)， 求10!

方法1：可以用python裡面的reduce函式，reduce() 函式會對引數序列中元素進行累積。

函式將一個數據集合（連結串列，元組等）中的所有資料進行下列操作：用傳給 reduce 中的函式 function（有兩個引數）先對集合中的第 1、2 個元素進行操作，得到的結果再與第三個資料用 function 函式運算，最後得到一個結果。

from functools import reduce

# 方法1：推薦！

a = 10
b = reduce(lambda x, y: x*y, range(1, a+1))
print(b)
 

如果不想用lamdba函式，可以定義一個函式

from functools import reduce

def chengfa(x, y):
    return x*y
a = 10
b = reduce(chengfa, range(1, a+1))
print(b)

方法2：自己寫個遞迴函式

def digui(n):
    if n == 1:
        return 1
    else:
        return n*digui(n-1)

a = 10
print(digui(a))

方法3：用for迴圈（不推薦！）

a = 10
s = 1
for i in range(1, a+1):
    s = s*i
print(s)
 

斐波那契數列

1. 已知一個數列：1、1、2、3、5、8、13、。。。。的規律為從3開始的每一項都等於其前兩項的和，這是斐波那契數列。求滿足規律的100以內的所以資料

a = 0
b = 1
while b < 100:
    print(b, end=",")
    a, b = b, a+b

冪的遞迴

計算x的n次方，如：3的4次方 為333*3=81

def mi(x, n):
    '''計算x 的n 次方'''
    if n == 0:
        return 1
    else:
        return x*mi(x, n-1)
x = 3
num = 4
print(mi(x, num))
 

漢諾塔問題

漢諾塔：漢諾塔（又稱河內塔）問題是源於印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。並且規定，在小圓盤上不能放大圓盤，在三根柱子之間一次只能移動一個圓盤

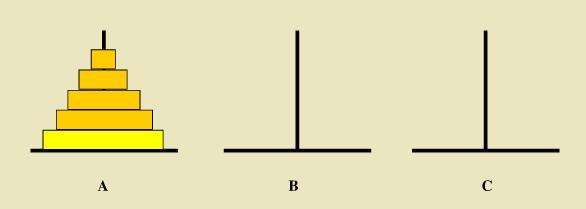
當只有一個盤子的時候，只需要從將A塔上的一個盤子移到C塔上。
當A塔上有兩個盤子是，先將A塔上的1號盤子（編號從上到下）移動到B塔上，再將A塔上的2號盤子移動的C塔上，最後將B塔上的小盤子移動到C塔上。
當A塔上有3個盤子時，先將A塔上編號1至2的盤子（共2個）移動到B塔上（需藉助C塔），然後將A塔上的3號最大的盤子移動到C塔，最後將B塔上的兩個盤子藉助A塔移動到C塔上。
當A塔上有n個盤子是，先將A塔上編號1至n-1的盤子（共n-1個）移動到B塔上（藉助C塔），然後將A塔上最大的n號盤子移動到C塔上，最後將B塔上的n-1個盤子藉助A塔移動到C塔上。
綜上所述，除了只有一個盤子時不需要藉助其他塔外，其餘情況均一樣（只是事件的複雜程度不一樣）。

def hanoi(n, a, b, c):
    '''漢諾塔問題'''
    if n == 1:
        print(a, '-->', c)
    else:
        hanoi(n - 1, a, c, b)
        print(a, '-->', c)
        hanoi(n - 1, b, a, c)

hanoi(5, 'A', 'B', 'C')