由於關於二叉樹的資料現在已經太多啦，那我們在這裡就直接貼程式碼，大家對應著註釋看就可以啦~~~

有一點要注意的是，二叉樹這裡建立時候的節點輸入順序要遵循從最左下開始逐漸向右哦~~

#include<iostream>
#include<malloc.h>
using namespace std;

typedef int data_type;

typedef struct A{
	A *left;
	A *right;
	data_type data ;
}Node;

//新建二叉樹 
Node *createNode(){
	
	Node *head;
	data_type tmp;
	cin>>tmp;
	
	if(tmp == 0)
	{
		head = NULL;
	}
	else                 
	{
		//遵循從左到右、從上到下的遞迴賦值原則 
		head = (Node *) malloc(sizeof(Node));
		head->data = tmp;
		head->left = createNode();
		head->right = createNode();
	}
	
	return head;
}

//二叉樹的遞迴先序遍歷方法 

Node Previous(Node *p)
{
	if(p)
	{
		cout<<p->data<<" ";
		Previous(p->left);
		Previous(p->right);
	}
	
}

//二叉樹的遞迴中序遍歷方法
Node Middle(Node *p)
{
	if(p)
	{
		Middle(p->left);
		cout<<p->data<<" ";
		Middle(p->right);	
	} 
} 

//二叉樹的遞迴後序遍歷方法

Node BackForward(Node *p) 
{
	if(p)
	{
		BackForward(p->left);
		BackForward(p->right);
	    cout<<p->data<<" ";	
	} 
}


//二叉樹的Morris中序遍歷方法 
Node MorrisMiddle(Node *p)
{

	//核心：通過兩個指標並藉助迴圈完成非遞迴的遍歷
	
	Node *p1 = p;
	Node *p2 = NULL;
	
	
	while(p1)
	{
		p2 = p1->left;
		
		//-------------------------------------------------
			if(p2)
		{
			
				while(p2->right && p2->right != p1)
				{
					//這裡就是要將p2置於右下節點位置的意思 
					p2 = p2->right;	
				}	
				
				if(!p2->right)
				{
					
					//將p1 p2間拉成類似雙向連結串列的結構，方便p1藉助p2完成回撥遍歷 
					p2->right = p1;
					p1 = p1->left;
					continue;
				}
		}
 
		cout<<p1->data<<" ";
	
		p1 = p1->right;
		
		//--------------------------------------------------
		//整體思想有點像是遞迴，但是由迴圈實現
	} 
	
}

//Morris前序遍歷法 


Node MorrisPrevious(Node *p)

{
		Node *p1 = p;
		Node *p2 = NULL;
	
	//開始根節點左側的遍歷 
	
	while(p1)
	{
		p2 = p1->left;
		
		//-------------------------------------------------
			if(p2)
		{
			
				while(p2->right && p2->right != p1)
				{
					//這裡就是要將p2置於右下節點位置的意思 
					p2 = p2->right;	
				}	
				
				if(!p2->right)
				{
					
					//將p1 p2間拉成類似雙向連結串列的結構，方便p1藉助p2完成回撥遍歷 
					p2->right = p1;
					cout<<p1->data<<" ";
					p1 = p1->left;
					continue;
				}
		}
		
			else
		{
			cout<<p1->data<<" ";
		}
			
		p1 = p1->right;
	} 
	
}

	//返回葉子節點的總數目 

	int LeafNumber(Node *p)
{	
        Node *head = p;
        
        if(!head)
        {
        	return 0;
		}
		
		else if(!head->left && !head->right)
		
			return 1;
		
		else
		
			return (LeafNumber(head->left)+LeafNumber(head->right));
			
}

	//返回二叉樹的深度
	
	int Deepth(Node *p)
{
		Node *head = p;
		
		if(head)
		{
			return Deepth(head->left)>=Deepth(head->right)?Deepth(head->left)+1:Deepth(head->right)+1;	
		}
		else
			return 0;		
} 

int main()
{
	//建立第一個樹 
	cout<<"Please input the binary tree: ";
	Node *root = createNode();
	
	//建立第二個樹 
	cout<<"Please input the binary tree: ";
	Node *root2 = createNode();
	
	cout<<endl<<"先序遞迴遍歷結果為：";
	Previous(root);
	
	cout<<endl<<"中序遞迴遍歷結果為：";
	Middle(root); 
	
	cout<<endl<<"後序遞迴遍歷結果為: ";
	BackForward(root);
	
		 
	cout<<endl<<"Tree1的葉子節點數目為: "<<LeafNumber(root);
	cout<<endl<<"Tree2的葉子節點數目為："<<LeafNumber(root2);
	
	cout<<endl<<"Tree1的深度為: "<<Deepth(root);
	cout<<endl<<"Tree2的深度為："<<Deepth(root2);
	
	cout<<endl<<endl<<"Morris中序遍歷的結果為: ";
	MorrisMiddle(root);

	cout<<endl<<"Morris先序遍歷的結果為: ";
	MorrisPrevious(root2);

} 
 

上文中沒有做的是Morris遍歷的後序法，由於這個方法對新手而言很不友好，在這裡我們秉著實用的原則，就先不與贅述啦。

感興趣的話歡迎自行去學習哦~~~

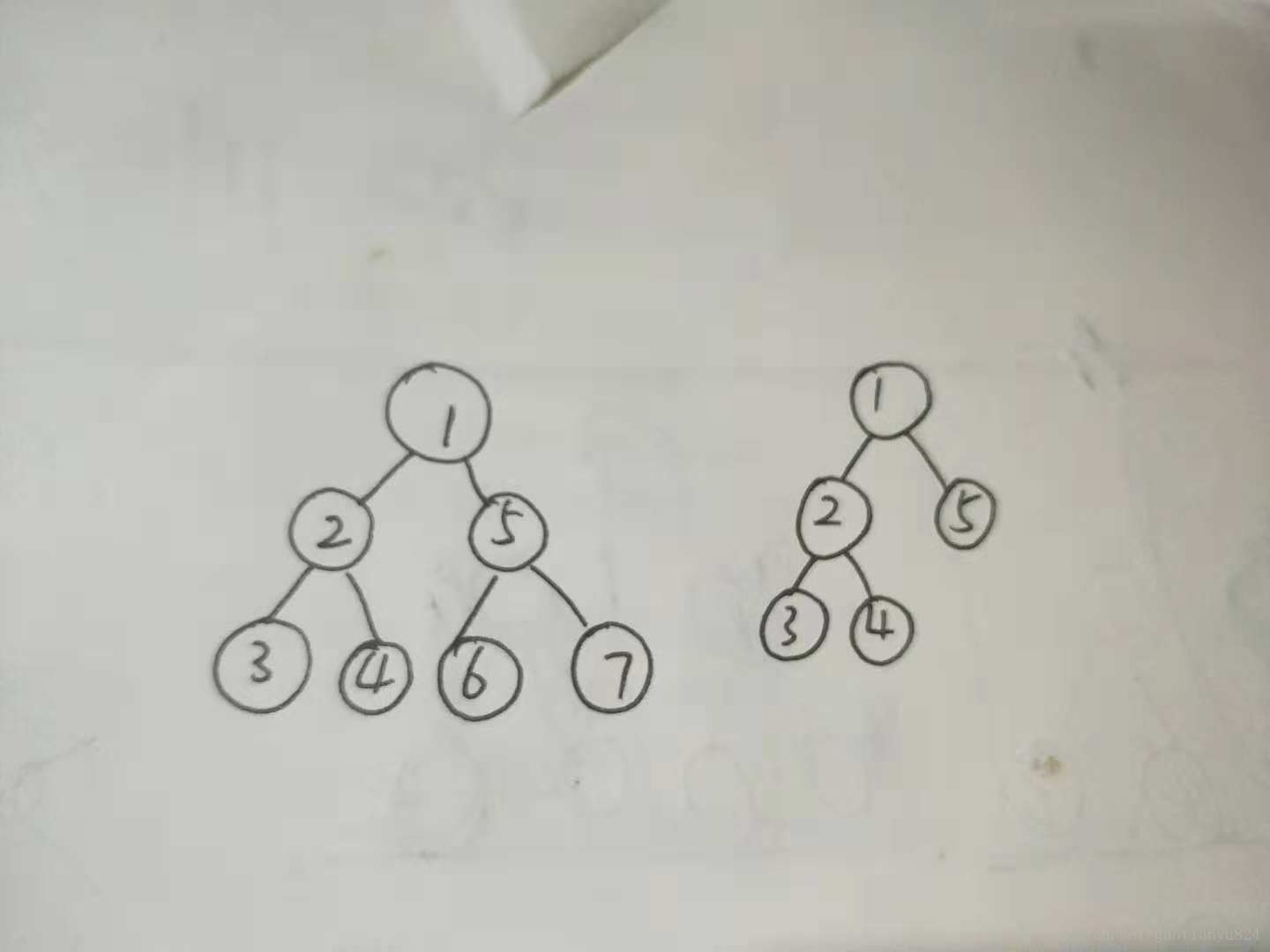
在這裡我們給出大家一組測試資料和對應結果——>