SciPy中稀疏矩陣的處理
在矩陣中,若數值為0的元素數目遠遠多於非0元素的數目,並且非0元素分佈沒有規律時,則稱該矩陣為稀疏矩陣。 ——來自百度百科。
為什麼會用到稀疏矩陣,最近在做協同過濾演算法時,呼叫評分圖和信任圖,資料的稀疏程度達到99.9%,這樣的資料儲存到記憶體中,0會佔據大量的記憶體,本想無所謂,但奈何記憶體放不下這樣的資料量,無奈進行稀疏矩陣的儲存與計算。記錄下學習筆記。
先舉一個小栗子,展示雙精度資料大小和記憶體之間的關係圖
import numpy as np import matplotlib.pyplot as plt x = np.linspace(0, 1e6, 10) plt.plot(x, 8.0 * (x**2) / 1e6, lw=5) plt.xlabel('size n') plt.ylabel('memory [MB]') plt.show()
顯示結果
稀疏矩陣的儲存:
稀疏矩陣作為一個矩陣,絕大多數都是0,為空。儲存所有的0是浪費。
所以想辦法進行壓縮。節省大量記憶體空間。
稀疏矩陣的視覺化圖(樣例):
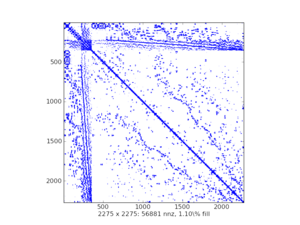
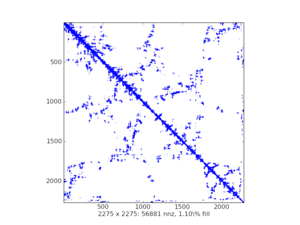
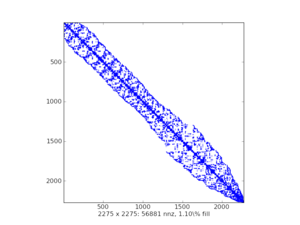
scipy.sparse中有七類稀疏矩陣:
csc_matrix: 壓縮列格式
csr_matrix: 壓縮行格式
bsr_matrix: 塊壓縮行格式
lil_matrix: 列表的列表格式
dok_matrix: 值的字典格式
coo_matrix: 座標格式 (即 IJV, 三維格式)
dia_matrix: 對角線格式
每一個型別適用於一些任務
許多都利用了由Nathan Bell提供的稀疏工具 C ++ 模組
-
- 算術操作的預設實現
- 通常轉化為CSR
- 為了效率而子類覆蓋
- 形狀、資料型別設定/獲取
- 非0索引
- 格式轉化、與Numpy互動(toarray(), todense())
- ...
- 算術操作的預設實現
-
屬性:
- mtx.A - 與mtx.toarray()相同
- mtx.T - 轉置 (與mtx.transpose()相同)
- mtx.H - Hermitian (列舉) 轉置
- mtx.real - 復矩陣的真部
- mtx.imag - 復矩陣的虛部
- mtx.size - 非零數 (與self.getnnz()相同)
- mtx.shape - 行數和列數 (元組)
- 資料通常儲存在Numpy陣列中
對角線格式 (DIA)
形狀 (n_diag, length) 的密集Numpy陣列的對角線。固定長度距離當離主對角線比較遠時會浪費空間。_data_matrix的子類 (帶資料屬性的稀疏矩陣類)
每個對角線的偏移:0 是主對角線,負偏移 = 下面,正偏移 = 上面
快速矩陣 * 向量 (sparsetools)(*代表矩陣相乘)
構建器接受 :1、密集矩陣 (陣列);2、稀疏矩陣;3、形狀元組 (建立空矩陣);4、(資料, 偏移) 元組
沒有切片、沒有單個專案訪問
用法 : 通過有限微分解偏微分方程;有一個迭代求解器
舉例DIA矩陣
【1】
import numpy as np
import scipy.sparse as sparse
import matplotlib.pyplot as plt
data = np.array([[1, 2, 3, 4]]).repeat(3, axis=0)
offsets = np.array([0, -1, 2])
mtx = sparse.dia_matrix((data, offsets), shape=(4, 4))
print(mtx)
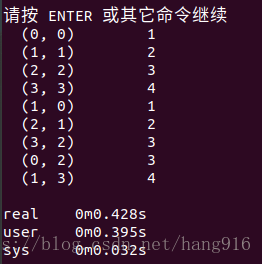
由此可以看出,mtx是一個4*4的矩陣,mtx的值,我是真不知道為什麼,跪求高人指點,網友說看下面的圖能看懂了,可能我腦回路有問題,我是真沒看懂。

【2】右圖為大神給的解釋圖,但是我還是有點問題
dia_matrix原始碼:
【3】矩陣相乘
列表格式(LIL)
基於行的連線列表。1、每一行是一個Python列表(排序的)非零元素的列索引;2、行儲存在Numpy陣列中 (dtype=np.object);3、非零值也近似儲存
高效增量構建稀疏矩陣
構建器接受 :1、密集矩陣 (陣列);2、稀疏矩陣;3、形狀元組 (建立一個空矩陣)
舉例LIL矩陣
【1】
【2】,更多的切片和索引
字典格式 (DOK)
Python字典的子類:1、鍵是 (行, 列) 索引元組 (不允許重複的條目);2、值是對應的非零值
高效增量構建稀疏矩陣
構建器支援:1、密集矩陣 (陣列);2、稀疏矩陣;3、形狀元組 (建立空矩陣)
高效 O(1) 對單個元素的訪問
一旦建立完成後可以被高效轉換為coo_matrix
算術很慢 (迴圈用dict.iteritems())
用法:當稀疏模式是未知的假設或改變時
座標格式 (COO)
稱為 ‘ijv’ 或 ‘triplet’ 格式:1、三個NumPy陣列: row, col, data;2、data[i]是在 (row[i], col[i]) 位置的值;3、允許重複值
構建稀疏矩陣的高速模式
構建器接受:1、密集矩陣 (陣列);2、稀疏矩陣;3、形狀元組 (建立空陣列);4、(data, ij)元組
可以與CSR/CSC格式非常快的互相轉換
快速的矩陣 * 向量 (sparsetools)
快速而簡便的逐項操作:直接操作資料陣列 (快速NumPy機制)
沒有切片,沒有算術 (直接)
使用:1、在各種稀疏格式間的靈活轉換;2、當轉化到其他形式 (通常是 CSR 或 CSC), 重複的條目被加總到一起
case【1】
行格式 (CSR)
面向行
三個Numpy陣列: indices, indptr, data
- indices是列索引的陣列
- data是對應的非零值陣列
- indptr指向indices和data開始的行
- 長度是n_row + 1, 最後一個專案 = 值數量 = indices和data的長度
- 第i行的非零值是列索引為indices[indptr[i]:indptr[i+1]]的data[indptr[i]:indptr[i+1]]
- 專案 (i, j) 可以通過data[indptr[i]+k], k是j在indices[indptr[i]:indptr[i+1]]的位置來訪問
快速矩陣向量相乘和其他算術 (sparsetools)
構建器接受:1、密集矩陣 (陣列);2、稀疏矩陣;3、形狀元組 (建立空矩陣);4、(data, ij) 元組;5、(data, indices, indptr) 元組
高效行切片,面向行的操作
較慢的列切片,改變稀疏結構代價昂貴
用途:
- 實際計算 (大多數線性求解器都支援這個格式)
case
【1】用(data, indices, indptr)元組建立:
解釋下mtx.indptr,mtx.indices
# 對於第i行,非0資料列是indices[indptr[i]:indptr[i+1]] 資料是data[indptr[i]:indptr[i+1]]
# 第0行,有非0的資料列是indices[indptr[0]:indptr[1]] = indices[0:2] = [0,2]
# 資料是data[indptr[0]:indptr[1]] = data[0:2] = [1,2],所以在第0行第0列是1,第0行第2列是2
# 第1行,有非0的資料列是indices[indptr[1]:indptr[2]] = indices[2:3] = [2]
# 資料是data[indptr[1]:indptr[2] = data[2:3] = [3],所以在第1行第2列是3
# 第2行,有非0的資料列是indices[indptr[2]:indptr[3]] = indices[3:6] = [0,1,2]
# 資料是data[indptr[2]:indptr[3]] = data[3:6] = [4,5,6],所以在第2行第0列是4,第2行第1行是5,第2行第2列是6
【2】用(data, ij)元組建立:
列格式 (CSC) (與CSR類似)
三個Numpy陣列: indices、indptr、data
- indices是行
- 索引的陣列
- data是對應的非零值
- indptr指向indices和data開始的列
- 長度是n_col + 1, 最後一個條目 = 值數量 = indices和data的長度
- 第i列的非零值是行索引為indices[indptr[i]:indptr[i+1]]的data[indptr[i]:indptr[i+1]]
- 專案 (i, j) 可以作為data[indptr[j]+k]訪問, k是i在indices[indptr[j]:indptr[j+1]]的位置
快速矩陣向量相乘和其他算術 (sparsetools)
構建器接受:1、密集矩陣 (陣列);2、稀疏矩陣;3、形狀元組 (建立空矩陣);4、(data, ij)元組;5、(data, indices, indptr)元組
高效列切片、面向列的操作
較慢的行切片、改變稀疏結構代價昂貴
用途:
- 實際計算 (巨大多數線性求解器支援這個格式)
case
【1】用(data, indices, indptr)元組建立:
解釋下mtx.indptr,mtx.indices
# 對於第i列,非0資料行是indices[indptr[i]:indptr[i+1]] 資料是data[indptr[i]:indptr[i+1]]
# 第0列,有非0的資料行是indices[indptr[0]:indptr[1]] = indices[0:2] = [0,2]
# 資料是data[indptr[0]:indptr[1]] = data[0:2] = [1,2],所以在第0列第0行是1,第0列第2行是2
# 第1列,有非0的資料行是indices[indptr[1]:indptr[2]] = indices[2:3] = [2]
# 資料是data[indptr[1]:indptr[2] = data[2:3] = [3],所以在第1列第2行是3
# 第2列,有非0的資料行是indices[indptr[2]:indptr[3]] = indices[3:6] = [0,1,2]
# 資料是data[indptr[2]:indptr[3]] = data[3:6] = [4,5,6],所以在第2列第0行是4,第2列第1行是5,第2列第2行是6
【2】用(data, ij)元組建立:
塊壓縮行格式 (BSR)
CSR帶有密集的固定形狀的子矩陣而不是純量的專案
塊大小(R, C)必須可以整除矩陣的形狀(M, N)
三個Numpy陣列: indices、indptr、data
- indices是每個塊列索引的陣列
- data是形狀為(nnz, R, C)對應的非零值
快速矩陣向量相乘和其他的算術 (sparsetools)
構建器接受:1、密集矩陣 (陣列);2、稀疏矩陣;3、形狀元組 (建立空的矩陣);4、(data, ij)元組;5、(data, indices, indptr)元組
許多對於帶有密集子矩陣的稀疏矩陣算術操作比CSR更高效很多
用途:
- 類似CSR
case
【1】用(data, ij)元組建立:
【2】用塊大小(data, indices, indptr)的元組建立:

















