交換類

• 氣泡排序（Bubble Sort） $O(n^2)$

最簡單的一種排序演算法。先從陣列中找到最大值(或最小值)並放到陣列最左端(或最右端)，然後在剩下的數字中找到次大值(或次小值)，以此類推，直到陣列有序排列。

void BubbleSortPlus(SqList L)
{
    int i, j, t, flag;
    flag = TRUE;

    for(i = 1; i <= L.length - 1 && flag; i++)
        for(j = 1; j <= L.length - 1 - i; j++)
 

        {
            flag = FALSE;
            if(L.elem[j] > L.elem[j+1])
            {
                t = L.elem[j];
                L.elem[j] = L.elem[j+1];
                L.elem[j+1] = t;
                flag = TRUE;
            }
        }
}

• 快速排序（Quick Sort）$O(nlgn)$（平均，最壞情況為氣泡排序）

快速排序的基本思想是：通過一趟排序將待排記錄分割成獨立的兩部分，其中一部分記錄的關鍵字均比另一部分記錄的關鍵字小，則可分別對這兩部分記錄繼續進行排序，已達到整個序列有序。一趟快速排序的具體過程可描述為：從待排序列中任意選取一個記錄(通常選取第一個記錄)作為基準值，然後將記錄中關鍵字比它小的記錄都安置在它的位置之前，將記錄中關鍵字比它大的記錄都安置在它的位置之後。這樣，以該基準值為分界線，將待排序列分成的兩個子序列。

void QuickSort(SqList L)
{
    QSort(L, 1, LENGTH);
}

void QSort(SqList &L, int low,
 
 int high)
{
    int pivotloc;
    if(low < high)
    {
        pivotloc = Partition(L, low, high);
        QSort(L, low, pivotloc - 1);
        QSort(L, pivotloc + 1 , high);
    }
}

int Partition(SqList &L, int low, int high)
{
    L.elem[0] = L.elem[low];

    while(low < high)
    {
        while(low < high && L.elem[high] >= L.elem[0])
        {
            high--;
        }
        L.elem[low] = L.elem[high];
        while(low < high && L.elem[high] <= L.elem[0])
        {
            low++;
        }
        L.elem[high] = L.elem[low];
    }

    L.elem[low] = L.elem[0];

    return low;
}

插入類

• 直接插入排序（Straight Insertion Sort） $O(n^2)$

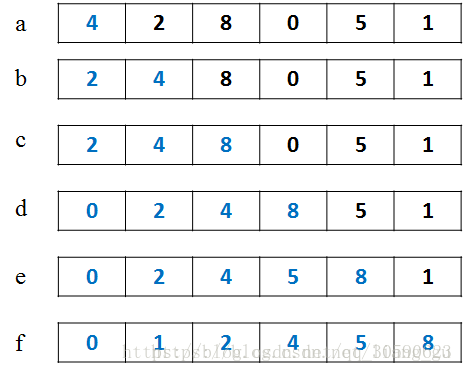
插入排序的基本思想就是將無序序列插入到有序序列中。例如要將陣列arr=[4,2,8,0,5,1]排序，可以將4看做是一個有序序列(圖中用藍色標出)，將[2,8,0,5,1]看做一個無序序列。無序序列中2比4小，於是將2插入到4的左邊，此時有序序列變成了[2,4]，無序序列變成了[8,0,5,1]。無序序列中8比4大，於是將8插入到4的右邊，有序序列變成了[2,4,8],無序序列變成了[0,5,1]。以此類推，最終陣列按照從小到大排序。

void InsertSort(SqList L)
{
    int i, j;
    
    for(i = 2; i <= L.length; i++)
    {
        if(L.elem[i] < L.elem[i-1])
        {
            L.elem[0] = L.elem[i];
            L.elem[i] = L.elem[i-1];
            for(j = i - 2; L.elem[0] < L.elem[j]; j--)
            {
                L.elem[j+1] = L.elem[j];
            }

            L.elem[j+1] = L.elem[0];
        }
    }
}

• 希爾排序（Shell Sort） $O(n^\frac{3}{2})$(較好情況）

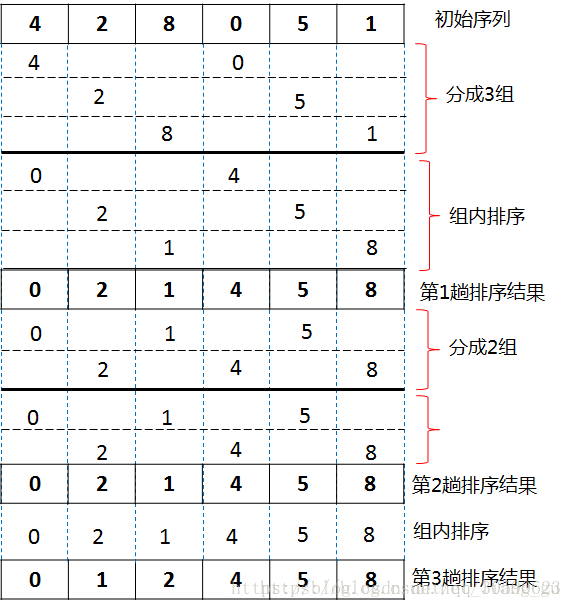
希爾排序(Shell Sort)在插入排序演算法的基礎上進行了改進，演算法的時間複雜度與前面幾種演算法相比有較大的改進。其演算法的基本思想是：先將待排記錄序列分割成為若干子序列分別進行插入排序，待整個序列中的記錄"基本有序"時，再對全體記錄進行一次直接插入排序。

void ShellSort(SqList L)
{
    int i, j, dk = L.length;
    
    do
    {
        dk = dk / 3 + 1;
        for(i = dk + 1; i <= L.length; i++)
        {
            if(L.elem[i] < L.elem[i-dk])
            {
                count1++;
                L.elem[0] = L.elem[i];  //L.elem[0]不是哨兵
                L.elem[i] = L.elem[i-dk];
                for(j = i - 2 * dk; j > 0 && L.elem[0] < L.elem[j]; j--)
                {
                    L.elem[j+dk] = L.elem[j];
                }

                L.elem[j+dk] = L.elem[0];

            }
        }
    }while(dk > 1);
}

選擇類

• 簡單選擇排序（Simple Selection Sort） $O(n^2)$

每一趟在n-i+1(i=1,2,…,n-1)個記錄中選取關鍵字最小的記錄作為有序序列中第i個記錄。

void InsertSort(SqList L)
{
    int i, j;

    for(i = 2; i <= L.length; i++)
    {
        if(L.elem[i] < L.elem[i-1])
        {
            L.elem[0] = L.elem[i];
            L.elem[i] = L.elem[i-1];
            for(j = i - 2; L.elem[0] < L.elem[j]; j--)
            {
                L.elem[j+1] = L.elem[j];
            }

            L.elem[j+1] = L.elem[0];
        }
    }
}

• 堆排序（Heap Sort） $O(nlgn)$

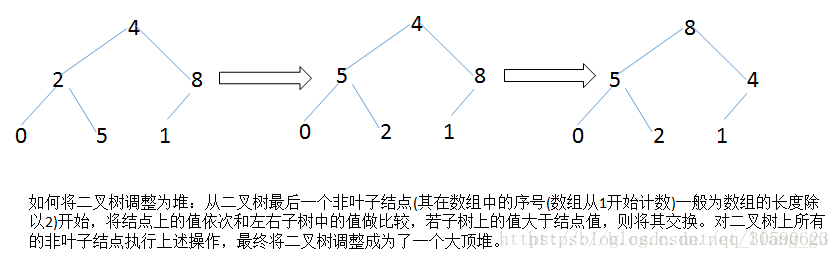
堆的定義如下: n個元素的序列{k1, k2, … , kn}當且僅當滿足一下條件時，稱之為堆。 $\begin{cases}k_i \leqslant k_{2i} & \qquad \qquad or & k_i \geqslant k_{2i} \\k_i \leqslant k_{2i+1} & & k_i \geqslant k_{2i+1} \\ &(i = 1, 2, ..., \lfloor n/2\rfloor)\end{cases}$ 堆排序(Heap Sort)是利用堆進行排序的方法。其基本思想為：將待排序列構造成一個大頂堆(或小頂堆)，整個序列的最大值(或最小值)就是堆頂的根結點，將根節點的值和堆陣列的末尾元素交換，此時末尾元素就是最大值(或最小值)，然後將剩餘的n-1個序列重新構造成一個堆，這樣就會得到n個元素中的次大值(或次小值)，如此反覆執行，最終得到一個有序序列。

void HeapSort(SqList L)
{
    int i, t;

    for(i = L.length / 2; i > 0; i--) //建堆
        HeapAdjust(L, i, L.length);

    for(i = L.length; i > 1; i--)
    {
        t = L.elem[1];
        L.elem[1] = L.elem[i];
        L.elem[i] = t;

        HeapAdjust(L, 1, i - 1);
    }
}

void HeapAdjust(SqList &L, int s, int m)
{
    int rc = L.elem[s], j;

    for(j = 2 * s; j <= m; j *= 2)
    {
        if(j < m && L.elem[j] < L.elem[j+1])
            j++;
        L.elem[s] = L.elem[j];
        s = j;
    }
    L.elem[s] = rc;
}

歸併類

• 歸併排序（Merge Sort） $O(nlgn)$（平均、最佳）

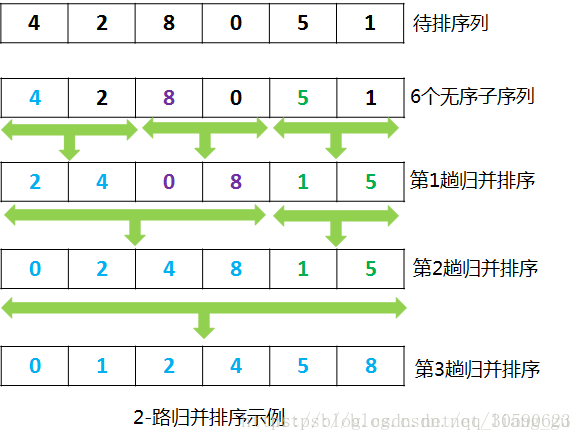
“歸併”的含義是將兩個或兩個以上的有序序列組合成一個新的有序表。假設初始序列含有n個記錄，則可以看成是n個有序的子序列，每個子序列的長度為1，然後兩兩歸併，得到$\lceil{n/2}\rceil$個長度為2(或者是1)的有序子序列，再兩兩歸併。如此重複，直到得到一個長度為n的有序序列為止。這種排序方法稱為2-路歸併排序。

void MergeSort(SqList L)
{
    MSort(L, 1, L.length);
}

void MSort(SqList &L, int low, int high)
{
    int mid;

    if(low < high)
    {
        mid = (low + high) / 2;
        MSort(L, low, mid);
        MSort(L, mid + 1, high);
        Merge(L, low, mid, high);
    }
}

void Merge(SqList &L, int low, int mid, int high)
{
    int m, n, i, j;
    m = mid - low + 1;
    n = high - mid;
    int M[m], N[n];

    for(i = 0; i < m; i++)
        M[i] = L.elem[low+i];
    for(j = 0; j < n; j++)
        N[j] = L.elem[mid+j+1];


    i = j = 0;

    while(i < m && j < n)
    {
        if(M[i] <= N[j])
            L.elem[low++] = M[i++];
        else
            L.elem[low++] = N[j++];
    }

    while(i < m)
    {
        L.elem[low++] = M[i++];
    }

    while(j < n)
    {
        L.elem[low++] = N[j++];
    }
}