吳恩達機器學習(十一)K-means(無監督學習、聚類演算法)
阿新 • • 發佈:2018-12-13
目錄
學習完吳恩達老師機器學習課程的無監督學習,簡單的做個筆記。文中部分描述屬於個人消化後的理解,僅供參考。
如果這篇文章對你有一點小小的幫助,請給個關注喔~我會非常開心的~
0. 前言
- 監督學習(supervised learning):樣本資料已經標記了所屬的類別
- 無監督學習(unsupervised learning):樣本資料未標記所屬的類別
無監督學習通常採用聚類演算法(clustering algorithm)對其分門別類,通常成為“簇”(cluster)。常見的聚類演算法有 K-means(K-均值),初始作如下定義:
--- 簇的數量
- --- 第
個樣本向量
--- 第
個樣本所屬的簇
--- 第
個簇中心的向量
--- 第
個樣本所屬的簇中心的向量
1. K-means的演算法流程
K-means主要由簇分配和移動聚類中心兩部分組成,是一種迭代的演算法,2個簇的流程可如下描述:
- 簇分配:隨機選擇兩個樣本點,作為簇中心,將每個樣本劃分至距離更近的簇中心,作為它所屬的簇
- 移動聚類中心:分別計算兩個簇中,屬於這個簇所有樣本的均值,將這個取平均後的向量位置作為當前簇新的中心
- 重新進行簇分配、移動聚類中心,不斷迭代,直到聚類中心不再改變
用虛擬碼,可作如下描述:
2. 代價函式(優化目標函式)
優化目標函式(代價函式)如下定義:
很明顯,代價函式表示的是,所有樣本與各自屬於的簇中心的歐式距離的平方和再取平均。
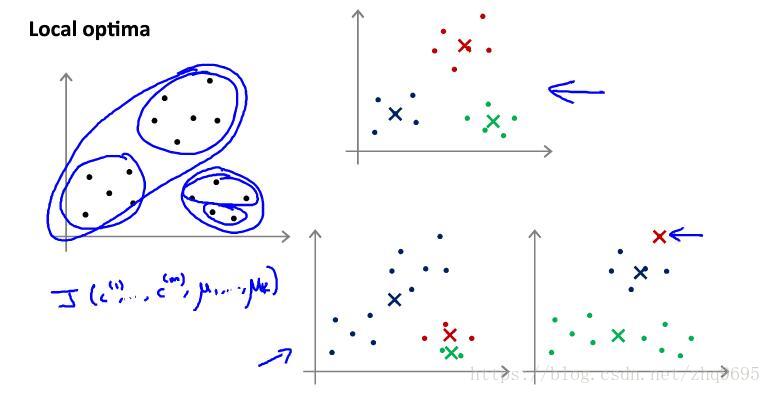
注:K-means聚類演算法有時候會陷入區域性最優解。
如下圖所示(圖源:吳恩達機器學習),就是一個區域性最優的例子:
為避免區域性最優,可在上述虛擬碼外再巢狀一層迴圈,每次確定簇中心之後計算代價函式,多次迭代之後,選擇代價函式最小的一組結果。此方法適合 值較小(小於10)的情況。
3. K 的選擇
簇的數量的選擇,通常有兩種方法,均要求 :
- 人工選擇:根據需求或者已知的知識,進行人工選擇簇的數量
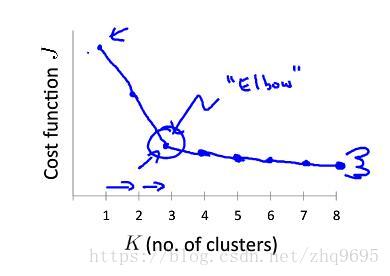
- 肘部法則:如下圖所示(圖源:吳恩達機器學習),嘗試不同的
,選擇變化率明顯變緩的“肘部點”
如果這篇文章對你有一點小小的幫助,請給個關注喔~我會非常開心的~