numpy

array與 python list很像

1.第一種建立方式可用np.array方法將list轉化成numpy array

import numpy as np
test_1=np.array([92, 94, 88, 91, 87])

my_list = [1, 2, 3, 4, 5, 6]
my_array = np.array(my_list)

第二種建立方式將csv匯入成array

test_2 = np.genfromtxt('test_2.csv', delimiter=',')

2.array相對於list的優越性

通過在陣列本身上執行操作，可以對陣列中的每個元素執行操作（例如新增）。

元素的加減乘除 冪 開方不需要for迴圈 可以直接進行

# With a list
l = [1, 2, 3, 4, 5]
l_plus_3 = []
for i in range(len(l)):
    l_plus_3.append(l[i] + 3)
# With an array
a = np.array(l)
a_plus_3 = a + 3

具有相同元素的array之間的相加可以直接進行，不是拼接，是每一個元素的相加這種，

import numpy as np

test_1 = np.array([92, 94, 88, 91, 87])
test_2 = np.array([79, 100, 86, 93, 91])
test_3 = np.array([87, 85, 72, 90, 92])
test_3_fixed = test_3 + 2
total_grade=test_1+test_2+test_3_fixed
final_grade=total_grade/3
print(final_grade)
 

同樣不用遍歷就能挑選出陣列中的值

import numpy as np

porridge = np.array([79, 65, 50, 63, 56, 90, 85, 98, 79, 51])

cold = porridge[porridge < 60]

hot = porridge[porridge > 80]

just_right = porridge[(porridge > 60) & (porridge < 80)]

print(cold)
print(hot)
print(just_right)

3.具有相同元素個數的陣列可以組成二維陣列 從二維陣列中取值類似一維

a =
np.array([[92, 94, 88, 91, 87],
          [79, 100, 86, 93, 91],
          [87, 85, 72, 90, 92]])

a[2,1]

#第一列
a[:,0]

#第一行
a[0,:]

4.function

1.mean

np.mean(array) 返回array的平均數

mean與邏輯運算 返回百分比 用mean而不是percentile

例如 np.mean(class_year>=2005) 返回陣列中大於2005 的比例 相當於百分比

二維陣列計算mean

axis=1 表示行平均數  axis=0表示列平均數

total_mean=np.mean(allergy_trials)
print(total_mean)

trial_mean=np.mean(allergy_trials,axis=1)
print(trial_mean)

patient_mean=np.mean(allergy_trials,axis=0)
print(patient_mean)

2.sort 可以找出異常值

np.sort(array) 返回一個排序好的array

3.Median 不受異常值影響

np.median(array) 返回array中位數 陣列元素個數為偶數則取中間兩個數平均數

4.percentile

一般來說一個array有五個節點0 25 50 75 100 

np.percentile(array,40) 返回百分之40處的數 因為median只能返回50%處的資料 所以要有percentile

5.Standard Deviation 標準差 標準差越大說明陣列與平均值相差越大

np.std(array) 返回標準差

6. np.random.normal(loc,scale,size) 隨機返回一組正態分佈的陣列

loc: 等於mean平均數  scale：等於標準差 size：次數

正態分佈一個標準差之內 也就是 mean+- std 一般是68% 兩個標準差97% 三個99%

7.np.random.binomial（N,P,size) 返回一組二項分佈的陣列 

二項分佈能有效幫助認識到時間發生的概率

N：樣本數量 P：成功概率 size:試驗次數

例： 向日葵不開花的概率為10 ，問200株向日葵栽下去，20朵一下不開花的概率

experiments=np.random.binomial(200,0.1,5000)
prob=np.mean(experiments<20)
print(prob)

ceballos競選市長問題 抽取的樣本越大  越接近真實數值，當在10000人中抽取7000人調查時基本就是真實情況 中心極限定理

import codecademylib
import numpy as np
from matplotlib import pyplot as plt

survey_responses = ['Ceballos', 'Kerrigan', 'Ceballos', 'Ceballos', 'Ceballos','Kerrigan', 'Kerrigan', 'Ceballos', 'Ceballos', 'Ceballos', 
'Kerrigan', 'Kerrigan', 'Ceballos', 'Ceballos', 'Kerrigan', 'Kerrigan', 'Ceballos', 'Ceballos', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Ceballos', 'Ceballos', 'Ceballos', 'Ceballos', 'Ceballos', 'Ceballos',
'Kerrigan', 'Kerrigan', 'Ceballos', 'Ceballos', 'Ceballos', 'Kerrigan', 'Kerrigan', 'Ceballos', 'Ceballos', 'Kerrigan', 'Kerrigan', 'Ceballos', 'Ceballos', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Ceballos',
'Kerrigan', 'Kerrigan', 'Ceballos', 'Ceballos', 'Ceballos', 'Kerrigan', 'Kerrigan', 'Ceballos', 'Ceballos', 'Kerrigan', 'Kerrigan', 'Ceballos', 'Ceballos', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Kerrigan', 'Ceballos']
total_ceballos=survey_responses.count('Ceballos')
print(total_ceballos)
percentage_ceballos=100*total_ceballos/len(survey_responses)
print(percentage_ceballos)

possible_surveys=np.random.binomial(70,0.54,size=10000)/70.
plt.hist(possible_surveys,range=(0,1), 
bins=20)
plt.show()
ceballos_loss_surveys=np.mean(possible_surveys<0.5)
print(ceballos_loss_surveys)
large_survey=np.random.binomial(7000,0.54,10000)/7000.
ceballos_loss_new=np.mean(large_survey<0.5)
print(ceballos_loss_new)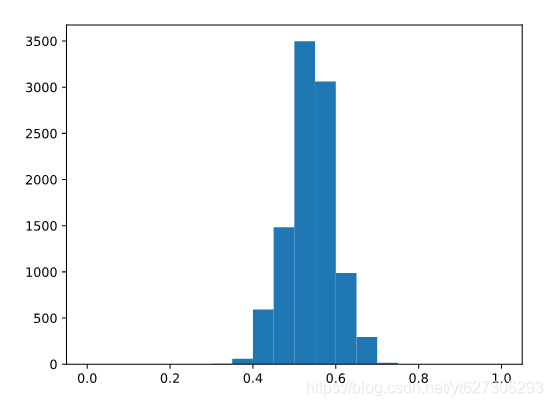

8.np.random.choice(array, size, replace=False)

從一組樣本衝隨機抽取size個成為新的樣本