決策樹(CART)
以下內容轉載來源:http://www.cnblogs.com/pinard/p/6053344.html
一、決策樹
1.決策樹與隨機森林都屬於機器學習中監督學習的範疇,主要用於分類問題。
決策樹演算法有這幾種:ID3、C4.5、CART(Classification And Regression Tree,二分決策樹 ),基於決策樹的演算法有bagging、隨機森林、GBDT等。
決策樹是一種利用樹形結構進行決策的演算法,對於樣本資料根據已知條件或叫特徵進行分叉,最終建立一棵樹,樹的葉子結節標識最終決策。新來的資料便可以根據這棵樹進行判斷。隨機森林是一種通過多棵決策樹進行優化決策的演算法。
引用別的文章的一個例子:
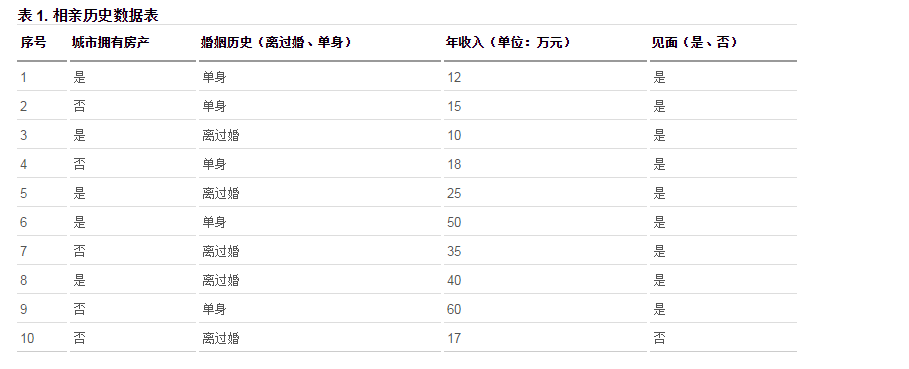
這是一張女孩對於不同條件的男性是否會選擇見面的統計表,圖中是否見面作為我們需要分類的結果,因此最後我們的結果無非就只是是和否兩種情況。這是一個二分類的問題,但是需要判斷的屬性有多個,首先選哪個屬性作為決策樹的根節點呢,決策樹怎麼構建呢。但是從上圖我們找到了一個結果為否的記錄,因此如果一個男性在城市無房產、年收入小於 17w 且離過婚,則可以預測女孩不會跟他見面。
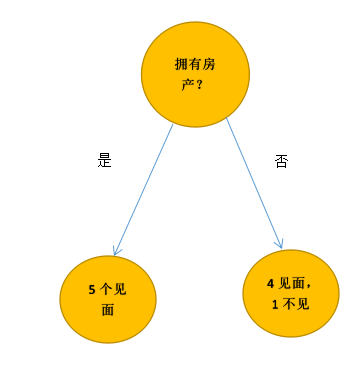
先通過城市是否擁有房產這條特徵,把這10個人劃分為2類
這個分類結果並不是很好,因為它沒有將見面與不見面完全的分開,在演算法中,當然不能憑我們的“感覺”去評價分類結果的好壞。我們需要用一個數去表示(即通過一個評價標準進行特徵選取)
二、CART分類樹演算法的最優特徵選擇方法
注:決策樹:在ID3演算法中使用資訊增益來選擇特徵,資訊增益大的優先選擇。在C4.5演算法中,採用了資訊增益比來選擇特徵,以減少資訊增益容易選擇特徵值多的特徵的問題,具體參見:https://www.cnblogs.com/pinard/p/6050306.html
CART分類樹演算法使用基尼係數來代替C4.5演算法中中的資訊增益比。(scikit-learn使用了優化版的CART演算法作為其決策樹演算法的實現)
基尼指數(基尼不純度):表示在樣本集合中一個隨機選中的樣本被分錯的概率。Gini指數越小表示集合中被選中的樣本被分錯的概率越小。也就是說集合的純度越高,特徵越好,反之,集合越不純。 (即基尼係數代表了模型的不純度,基尼係數越小,則不純度越低,特徵越好)
即 基尼指數(基尼不純度)= 樣本被選中的概率 * 樣本被分錯的概率
具體的,在分類問題中,假設有K個類別,第k個類別的概率為![]() , 則基尼係數的表示式為:
, 則基尼係數的表示式為:
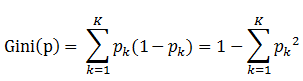
如果是二類分類問題,計算就更加簡單了,如果屬於第一個樣本輸出的概率是p,則基尼係數的表示式為: Gini(P)=2P(1-P)
對於個給定的樣本D,假設有K個類別, 第k個類別的數量為![]() ,則樣本D的基尼係數表示式為:
,則樣本D的基尼係數表示式為:
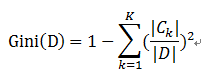
特別的,對於樣本D,如果根據特徵A的某個值a,把D分成D1和D2兩部分,則在特徵A的條件下,D的基尼係數表示式為:
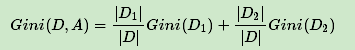
注:為了進一步簡化,CART分類樹演算法每次僅僅對某個特徵的值進行二分,而不是多分,這樣CART分類樹演算法建立起來的是二叉樹,而不是多叉樹。這樣一可以進一步簡化基尼係數的計算,二可以建立一個更加優雅的二叉樹模型。
例子如下:
對於上述的結果來講(先通過城市是否擁有房產這條特徵,把這10個人劃分為2類),總的集合D被分為兩個集合D1,D2,假設見面為1,不見面為0。
那麼D1的不純度為1-f1^2-f0^2,總數為5,見面的佔了全部,則f1=1,f0=0,結果為0
D2的不純度為1-f1^2-f0^2,f1=0.8,f0=0.2,結果為0.32 (2*f1*f0(f0即為1-![]() ))
))
那麼整個分類結果的Gini不純度就是D1/D與0的乘積 加上 D2/D與0.32的乘積,為0.16
Gini值代表了某一個分類結果的“純度”,我們希望結果的純度很高,這樣就不需要對這一結果進行處理了。
從以上分析可以看出,Gini值越小,純度越高,結果越好
三、CART分類樹演算法對於連續特徵和離散特徵處理的改進
對於CART分類樹連續值的處理問題,其思想和C4.5是相同的,都是將連續的特徵離散化。唯一的區別在於在選擇劃分點時的度量方式不同,C4.5使用的是資訊增益比,則CART分類樹使用的是基尼係數。
具體的思路如下,比如m個樣本的連續特徵A有m個,從小到大排列為![]() ,則CART演算法取相鄰兩樣本值的平均數,一共取得m-1個劃分點,其中第i個劃分點Ti表示Ti表示為:
,則CART演算法取相鄰兩樣本值的平均數,一共取得m-1個劃分點,其中第i個劃分點Ti表示Ti表示為:![]() 。對於這m-1個點,分別計算以該點作為二元分類點時的基尼係數。選擇基尼係數最小的點作為該連續特徵的二元離散分類點。比如取到的基尼係數最小的點為
。對於這m-1個點,分別計算以該點作為二元分類點時的基尼係數。選擇基尼係數最小的點作為該連續特徵的二元離散分類點。比如取到的基尼係數最小的點為![]() ,則小於
,則小於![]() 的值為類別1,大於
的值為類別1,大於![]() 的值為類別2,這樣我們就做到了連續特徵的離散化。要注意的是,與ID3或者C4.5處理離散屬性不同的是,如果當前節點為連續屬性,則該屬性後面還可以參與子節點的產生選擇過程。
的值為類別2,這樣我們就做到了連續特徵的離散化。要注意的是,與ID3或者C4.5處理離散屬性不同的是,如果當前節點為連續屬性,則該屬性後面還可以參與子節點的產生選擇過程。
對於CART分類樹離散值的處理問題,採用的思路是不停的二分離散特徵。例如:回憶下ID3或者C4.5,如果某個特徵A被選取建立決策樹節點,如果它有A1,A2,A3三種類別,我們會在決策樹上一下建立一個三叉的節點。這樣導致決策樹是多叉樹。但是CART分類樹使用的方法不同,他採用的是不停的二分,CART分類樹會考慮把A分成{A1}和{A2,A3}{A1}和{A2,A3}, {A2}和{A1,A3}{A2}和{A1,A3}, {A3}和{A1,A2}{A3}和{A1,A2}三種情況,找到基尼係數最小的組合,比如{A2}和{A1,A3}{A2}和{A1,A3},然後建立二叉樹節點,一個節點是A2對應的樣本,另一個節點是{A1,A3}對應的節點。同時,由於這次沒有把特徵A的取值完全分開,後面我們還有機會在子節點繼續選擇到特徵A來劃分A1和A3。這和ID3或者C4.5不同,在ID3或者C4.5的一棵子樹中,離散特徵只會參與一次節點的建立。
四、CART分類樹建立演算法的具體流程
上面介紹了CART演算法的一些和C4.5不同之處,下面我們看看CART分類樹建立演算法的具體流程,之所以加上了建立,是因為CART樹演算法還有獨立的剪枝演算法這一塊(見第六小節)
演算法輸入是訓練集D,基尼係數的閾值,樣本個數閾值。
輸出是決策樹T。
我們的演算法從根節點開始,用訓練集遞迴的建立CART樹。
1) 對於當前節點的資料集為D,如果樣本個數小於閾值或者沒有特徵,則返回決策子樹,當前節點停止遞迴。
2) 計算樣本集D的基尼係數,如果基尼係數小於閾值,則返回決策樹子樹,當前節點停止遞迴。
3) 計算當前節點現有的各個特徵的各個特徵值對資料集D的基尼係數,對於離散值和連續值的處理方法和基尼係數的計算見第三節。缺失值的處理方法(這裡就不詳述了,其可參見C4.5演算法的處理)。
4) 在計算出來的各個特徵的各個特徵值對資料集D的基尼係數中,選擇基尼係數最小的特徵A和對應的特徵值a。根據這個最優特徵和最優特徵值,把資料集劃分成兩部分D1和D2,同時建立當前節點的左右節點,做節點的資料集D為D1,右節點的資料集D為D2.
5) 對左右的子節點遞迴的呼叫1-4步,生成決策樹。
對於生成的決策樹做預測的時候,假如測試集裡的樣本A落到了某個葉子節點,而節點裡有多個訓練樣本。則對於A的類別預測採用的是這個葉子節點裡概率最大的類別。
五、CART迴歸樹建立演算法
CART迴歸樹和CART分類樹的建立演算法大部分是類似的,這裡討論不同的地方。
首先,我們要明白,什麼是迴歸樹,什麼是分類樹。兩者的區別在於樣本輸出,如果樣本輸出是離散值,那麼這是一顆分類樹。如果樣本輸出是連續值,那麼這是一顆迴歸樹。
除了概念的不同,CART迴歸樹和CART分類樹的建立和預測的區別主要有下面兩點:
1)連續值的處理方法不同
2)決策樹建立後做預測的方式不同。
對於連續值的處理,我們知道CART分類樹採用的是用基尼係數的大小來度量特徵的各個劃分點的優劣情況。這比較適合分類模型,但是對於迴歸模型,我們使用了常見的均方差的度量方式,CART迴歸樹的度量目標是,對於任意劃分特徵A,對應的任意劃分點s兩邊劃分成的資料集D1和D2,求出使D1和D2各自集合的均方差最小,同時D1和D2的均方差之和最小所對應的特徵和特徵值劃分點。表示式為:
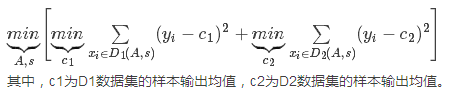
對於決策樹建立後做預測的方式,上面講到了CART分類樹採用葉子節點裡概率最大的類別作為當前節點的預測類別。而回歸樹輸出不是類別,它採用的是用最終葉子的均值或者中位數來預測輸出結果。
六、CART樹演算法的剪枝
由於決策時演算法很容易對訓練集過擬合,而導致泛化能力差,為了解決這個問題,我們需要對CART樹進行剪枝,即類似於線性迴歸的正則化,來增加決策樹的泛化能力。但是,有很多的剪枝方法,我們應該這麼選擇呢?CART採用的辦法是後剪枝法,即先生成決策樹,然後產生所有可能的剪枝後的CART樹,然後使用交叉驗證來檢驗各種剪枝的效果,選擇泛化能力最好的剪枝策略。
也就是說,CART樹的剪枝演算法可以概括為兩步,第一步是從原始決策樹生成各種剪枝效果的決策樹,第二部是用交叉驗證來檢驗剪枝後的預測能力,選擇泛化預測能力最好的剪枝後的數作為最終的CART樹。
首先我們看看剪枝的損失函式度量,在剪枝的過程中,對於任意的一刻子樹T,其損失函式為:
![]()
未完待續,後期進行補充…………
七、CART演算法小結
上面我們對CART演算法做了一個詳細的介紹,CART演算法相比C4.5演算法的分類方法,採用了簡化的二叉樹模型,同時特徵選擇採用了近似的基尼係數來簡化計算。當然CART樹最大的好處是還可以做迴歸模型,這個C4.5沒有。下表給出了ID3,C4.5和CART的一個比較總結。
| 演算法 | 支援模型 | 樹結構 | 特徵選擇 | 連續值處理 | 缺失值處理 | 剪枝 |
| ID3 | 分類 | 多叉樹 | 資訊增益 | 不支援 | 不支援 | 不支援 |
| C4.5 | 分類 | 多叉樹 | 資訊增益比 | 支援 | 支援 | 支援 |
| CART | 分類,迴歸 | 二叉樹 | 基尼係數,均方差 | 支援 | 支援 | 支援 |
看起來CART演算法高大上,那麼CART演算法還有沒有什麼缺點呢?有!主要的缺點我認為如下:
1)應該大家有注意到,無論是ID3, C4.5還是CART,在做特徵選擇的時候都是選擇最優的一個特徵來做分類決策,但是大多數,分類決策不應該是由某一個特徵決定的,而是應該由一組特徵決定的。這樣決策得到的決策樹更加準確。這個決策樹叫做多變數決策樹(multi-variate decision tree)。在選擇最優特徵的時候,多變數決策樹不是選擇某一個最優特徵,而是選擇最優的一個特徵線性組合來做決策。這個演算法的代表是OC1,這裡不多介紹。
2)如果樣本發生一點點的改動,就會導致樹結構的劇烈改變。這個可以通過整合學習裡面的隨機森林之類的方法解決。