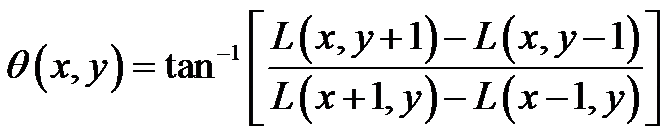Sift之前的江湖

在Sift橫空出世之前，特徵點檢測與匹配江湖上佔據霸主地位的是角點檢測家族。先來探究一下角點家族不為人知的恩怨情仇。

角點家族的族長是Moravec在1977年提出的Moravec角點檢測運算元，它是一種基於灰度方差的角點檢測方法，該運算元計算影象中某個畫素點沿水平、垂直方向上的灰度差異，以確定角點位置，Moravec是第一個角點檢測演算法，也是角點家族的開山鼻祖。

角點家族的九袋長老是Chris Harris & Mike Stephens在1988年提出的Harris角點檢測運算元。Harris不止是考察水平、垂直4個方向上的灰度差異，而是考察了所有方向上的灰度差異，並且具有旋轉不變性和對部分仿射變換的穩定性。Harris是整個角點檢測家族的顏值擔當。

角點家族的大護法是J.Shi和C.Tomasi在1994年提出的Shi-Tomasi角點檢測運算元，它是對Harris角點運算元的改進，並且有一個直接“叫囂”Harris運算元的名字——“Good Features to Track”，在Opencv中實現函式是goodfeaturesToTrack。它通過考察自相關矩陣M的兩個特徵值中的較小者來確定就角點，大部分情況下，有比Harris更好的檢測效果。

角點家族洪興堂堂主是E.Rosten和T.Drummond在2006年提出的FAST(Feature from Accelerated Segment Test)運算元。它通過考察畫素點與其鄰域內16個畫素點的差異來確定特徵點（角點），並且通過分割測試演算法對檢測效率做了極大的提升。它信奉“天下武功，唯快不破”的真理，在快的道路上銳意進取，基本可以滿足實時檢測系統的要求，在現今計算機視覺領域賺足了眼球。

角點家族這種群雄逐鹿的局面一直持續了很多年，大家你追我趕，在群主Moravec的帶領下家族基於日漸殷實。直到20多年後的1999年的某天拂曉，一個叫Sift的後生叩響了角點家族的鎏金鐵門。

Sift閃亮登場

1999年，大不列顛哥倫比亞大學的David G.Lowe教授在現有基於不變數技術的特徵檢測方法基礎上，提出了一種基於尺度空間的，對影象縮放、旋轉、甚至仿射變換保持不變性的影象區域性特徵描述運算元——Sift（尺度不變特徵變換），全稱是Scale Invariant Feature Transform，並且在2004年，又對Sift演算法做了更為系統的完善。下邊這位老爺子就是Lowe。

Sift提取影象的區域性特徵，在尺度空間尋找極值點，並提取出其位置、尺度、方向資訊。Sfit的應用範圍包括物體辨別、機器人地圖感知與導航、影響拼接、3D模型建立、手勢識別、影響追蹤等。

Sift特徵的特點：

1. 對旋轉、尺度縮放、亮度變化保持不變性，對視角變化、噪聲等也存在一定程度的穩定性；

2. 獨特性，資訊量豐富，適用於在海量特徵資料中進行快速，準確的匹配；

3. 多量性，即使少數幾個物體也可以產生大量的Sfit特徵向量；

4. 可擴充套件性，可以很方便的與其他形式的特徵向量進行聯合；

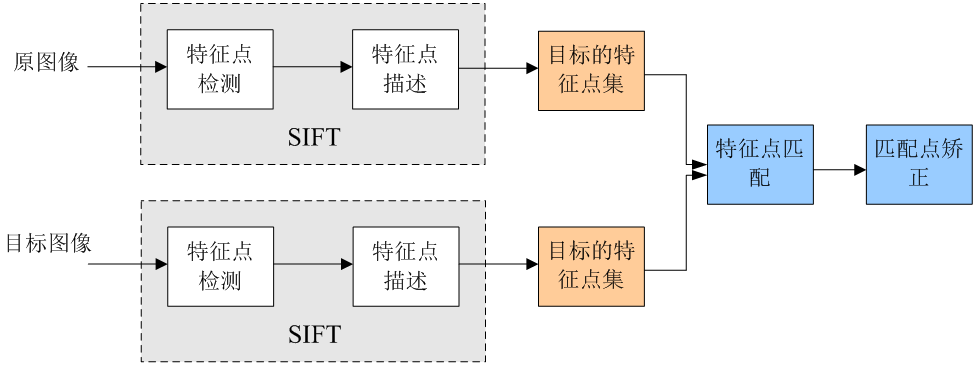
Sfit演算法的實質是在不同的尺度空間上查詢關鍵點（特徵點），計算關鍵點的大小、方向、尺度資訊，利用這些資訊組成關鍵點對特徵點進行描述的問題。Sift所查詢的關鍵點都是一些十分突出，不會因光照，仿射便函和噪聲等因素而變換的“穩定”特徵點，如角點、邊緣點、暗區的亮點以及亮區的暗點等。匹配的過程就是對比這些特徵點的過程，這個流程可以用下圖表述：

Sfit特徵提取和匹配具體步驟

1. 生成高斯差分金字塔（DOG金字塔），尺度空間構建

2. 空間極值點檢測（關鍵點的初步查探）

3. 穩定關鍵點的精確定位

4. 穩定關鍵點方向資訊分配

5. 關鍵點描述

6. 特徵點匹配

以下對這6個步驟逐一說明。

1. 生成高斯差分金字塔（DOG金字塔），尺度空間構建

主要思想是通過對原始影象進行尺度變換，獲得影象多尺度下的尺度空間表示序列，對這些序列進行尺度空間主輪廓的提取，並以該主輪廓作為一種特徵向量，實現邊緣、角點檢測不同解析度上的關鍵點提取等。

各尺度下影象的模糊度逐漸變大，能夠模擬人在距離目標由近到遠時目標物體在視網膜上的形成過程。

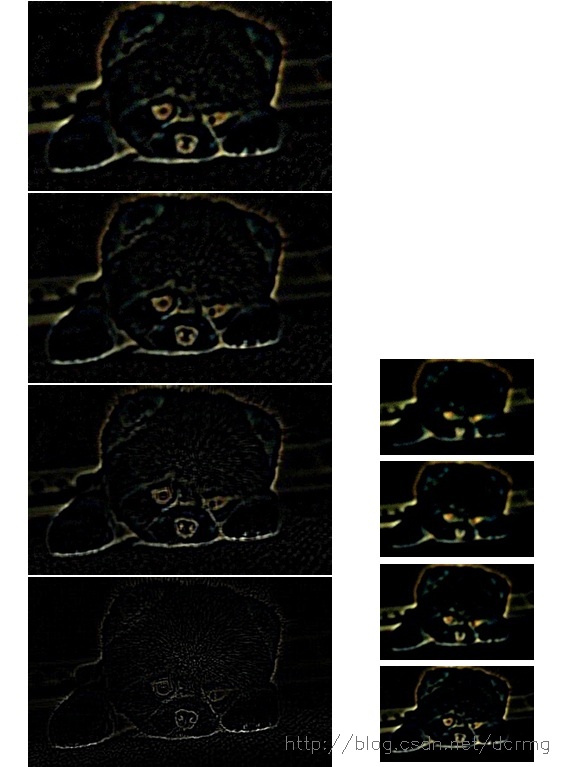
尺度空間構建的基礎是DOG金字塔，DOG金字塔構建的基礎是高斯金字塔，關於尺度空間、高斯金字塔、DOG金字塔的相關說明，可以參看前一篇博文《Sift中尺度空間、高斯金字塔、差分金字塔（DOG金字塔）、影象金字塔》。貼一下高斯金字塔的例項影象：

歸一化的DOG金字塔例項影象：

2. 空間極值點檢測（關鍵點的初步查探）

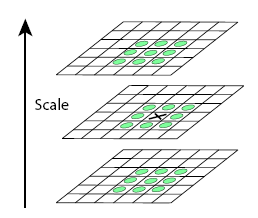
為了尋找DOG函式的極值點，每一個畫素點要和它所有的相鄰點比較，看其是否比它的影象域和尺度空間域的相鄰點大或者小，如下圖所示：

在二維影象空間，中心點與它3*3鄰域內的8個點做比較，在同一組內的尺度空間上，中心點和上下相鄰的兩層影象的2*9個點作比較，如此可以保證檢測到的關鍵點在尺度空間和二維影象空間上都是區域性極值點。

3. 穩定關鍵點的精確定位

DOG值對噪聲和邊緣比較敏感，所以在第2步的尺度空間中檢測到的區域性極值點還要經過進一步的篩選，去除不穩定和錯誤檢測出的極值點，另一點就是在構建高斯金字塔過程中採用了下采樣的影象，在下采樣影象中提取的極值點對應在原始影象中的確切位置，也是要在本步驟中解決的問題。

4. 穩定關鍵點方向資訊分配

穩定的極值點是在不同尺度空間下提取的，這保證了關鍵點的尺度不變性。為關鍵點分配方向資訊所要解決的問題是使得關鍵點對影象角度和旋轉具有不變性。方向的分配是通過求每個極值點的梯度來實現的。

對於任一關鍵點，其梯度幅值表述為：

梯度方向為：

分配給關鍵點的方向並不直接是關鍵點的梯度方向，而是按照一種梯度方向直方圖的方式給出的。

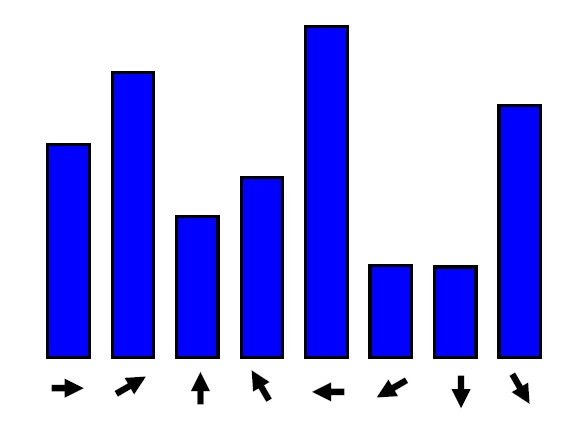
具體的方法是：計算以關鍵點為中心的鄰域內所有點的梯度方向，當然梯度方向一定是在0~360°範圍內，對這些梯度方向歸一化到36個方向內，每個方向代表了10°的範圍。然後累計落到每個方向內的關鍵點個數，以此生成梯度方向直方圖。

將梯度方向直方圖中縱座標最大的項代表的方向分配給當前關鍵點作為主方向，若在梯度直方圖中存在一個相當於主峰值80%能量的峰值，則將這個方向認為是關鍵點的輔方向。輔方向的設計可以增強匹配的魯棒性，Lowe指出，大概有15%的關鍵點具有輔方向，而恰恰是這15%的關鍵點對穩定匹配起到關鍵作用。

5. 關鍵點描述

對關鍵點的描述是後續實現匹配的關鍵步驟，描述其實就是一種以數學方式定義關鍵的過程。描述子不但包含關鍵點，也包括關鍵點周圍對其有貢獻的鄰域點。

描述的思路是：對關鍵點周圍畫素區域分塊，計算快內梯度直方圖，生成具有獨特性的向量，這個向量是該區域影象資訊的一種抽象表述。

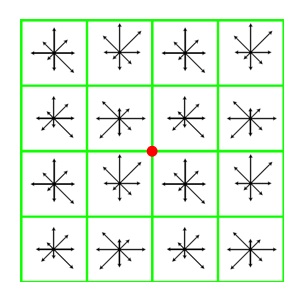
如下圖，對於2*2塊，每塊的所有畫素點的荼毒做高斯加權，每塊最終取8個方向，即可以生成2*2*8維度的向量，以這2*2*8維向量作為中心關鍵點的數學描述。

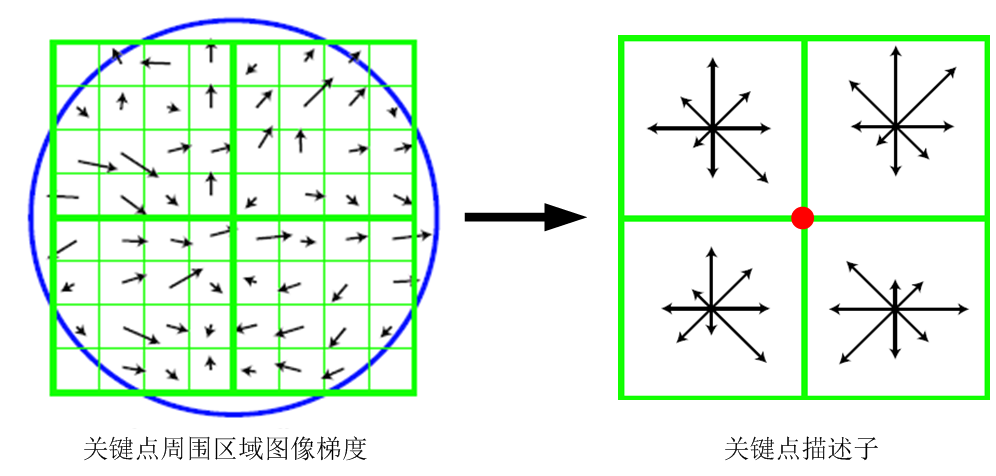
David G.Lowed的實驗結果表明：對每個關鍵點，採用4*4*8共128維向量的描述子進項關鍵點表徵，綜合效果最佳：

6. 特徵點匹配

特徵點的匹配是通過計算兩組特徵點的128維的關鍵點的歐式距離實現的。歐式距離越小，則相似度越高，當歐式距離小於設定的閾值時，可以判定為匹配成功。

Sift特徵匹配效果：

--------------------- 本文來自 -牧野- 的CSDN 部落格 ，全文地址請點選：https://blog.csdn.net/dcrmg/article/details/52577555?utm_source=copy