氣泡排序(雞尾酒排序)的Java實現
氣泡排序
-
基本思想: 兩兩比較相鄰記錄的關鍵字,如果反序則交換,直到沒有反序的記錄為止。
-
演算法步驟: (1)從陣列中第一個數開始,依次與下一個數比較並次交換比自己小的數,直到最後一個數。如果發生交換,則繼續下面的步驟,如果未發生交換,則陣列有序,排序結束,此時時間複雜度為O(n); (2)每一輪“冒泡”結束後,最大的數將出現在亂序數列的最後一位。重複步驟(1)。
-
時間複雜度: O(n)至O(n2),平均時間複雜度為O(n2)。 最好的情況:如果待排序資料序列為正序,則一趟冒泡就可完成排序,排序碼的比較次數為n-1次,且沒有移動,時間複雜度為O(n)。 最壞的情況:如果待排序資料序列為逆序,則氣泡排序需要n-1次趟起泡,每趟進行n-i次排序碼的比較和移動,即比較和移動次數均達到最大值: 比較次數:Cmax=∑i=1n−1(n−i)=n(n−1)/2=O(n2) 移動次數等於比較次數,因此最壞時間複雜度為O(n2)。
程式碼實現:
public class BubbleSort { public static void main(String[] args) { System.out.println("=============第一版本=============="); int[] arr ={11,95,45,15,51,12,24}; sort1(arr); System.out.println("=============第二版本=============="); arr = new int[]{11,95,45,15,51,12,24}; sort2(arr); System.out.println("=============雞尾酒排序=============="); arr = new int[]{11,95,45,15,51,12,24}; sort3(arr); } //第三版本,雞尾酒排序演算法 public static void sort3(int[] arr){ boolean sorted1 = true; boolean sorted2 = true; int len = arr.length; for(int j=0; j<len/2; j++){ //趟數 sorted1 = true; //假定有序 sorted2 = true; for(int i=0; i<len-1-j; i++){ //次數 if(arr[i] > arr[i+1]){ int temp = arr[i]; arr[i] = arr[i+1]; arr[i+1] = temp; sorted1 = false; //假定失敗 } } for(int i=len-1-j; i>j; i--){ //次數 if(arr[i] < arr[i-1]){ int temp = arr[i]; arr[i] = arr[i+1]; arr[i+1] = temp; sorted2 =false; //假定失敗 } } System.out.println(Arrays.toString(arr)); if(sorted1 && sorted2){ //減少趟數,已有序則結束 break; } } } //第二版本,減少每一趟的次數 public static void sort2(int[] arr){ boolean sorted= true; int len =arr.length; for(int j=0;j<len-1;j++){ //趟數 sorted =true; //假定有序 for(int i=0;i<len-1-j;i++){ //次數 if(arr[i]>arr[i+1]){ int temp = arr[i]; arr[i] = arr[i+1]; arr[i+1] = temp; sorted =false; //假定失敗 } } System.out.println(Arrays.toString(arr)); if(sorted){ //減少趟數 break; } } } //第一版本,簡單的實現氣泡排序 public static void sort1(int[] arr){ int len =arr.length; for(int j=0;j<len-1;j++){ //趟數 System.out.println("第"+(j+1)+"趟"); for(int i=0;i<len-1-j;i++){ //次數 System.out.print("第"+(i+1)+"次"); if(arr[i]>arr[i+1]){ int temp = arr[i]; arr[i] = arr[i+1]; arr[i+1] = temp; } System.out.println(Arrays.toString(arr)); } } } }
執行結果如下:

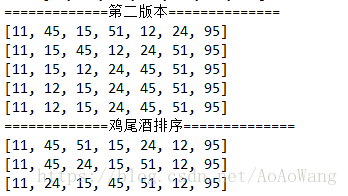
雞尾酒排序
-
雞尾酒排序演算法 基本思想:陣列中的數字本是無規律的排放,先找到最小的數字,把他放到第一位,然後找到最大的數字放到最後一位。然後再找到第二小的數字放到第二位,再找到第二大的數字放到倒數第二位。以此類推,直到完成排序。 雞尾酒排序的時間複雜度與氣泡排序相同。
-
雞尾酒排序與氣泡排序的區別 雞尾酒排序等於是氣泡排序的輕微變形。不同的地方在於從低到高然後從高到低,而氣泡排序則僅從低到高去比較序列裡的每個元素。他可以得到比氣泡排序稍微好一點的效能,原因是氣泡排序只從一個方向進行比對(由低到高),每次迴圈只移動一個專案。 以序列(2,3,4,5,1)為例,雞尾酒排序只需要訪問兩次(升序降序各一次 )次序列就可以完成排序,但如果使用氣泡排序則需要四次。
