Tip：各平臺的 markdown 解析標準不同，會有些數學符號無法識別，比如^n^: 表示n次方，~y~: 表示y 的底數。

什麼是複雜度分析?

演算法複雜度是指演算法在編寫成可執行程式後，執行時所需要的資源，資源包括時間資源和記憶體資源。

為什麼需要複雜度分析？

首先任何一個程式最重要是準確性，即要確保程式能正常執行，實現預期功能。
但是，任何一個有價值的程式除了確保能正常執行，還要確保儘量短的執行時間和儘量少的執行空間，使程式正確高效執行得到預期效果。這就涉及時間複雜度分析和（空間複雜度分析），通過分析程式演算法的時間複雜度可以找出執行時間儘量短的演算法。

對於一些資料處理比較少的簡單程式，不同演算法使程式執行時間不同，但由於資料處理量少，這種執行時間的差別可以忽略。但是在實際應用中，很多程式往往涉及相當大量的資料處理，這就會導致實現同一個功能的程式，用不同演算法，執行時間差別很大。有些演算法可能只要幾秒，有些演算法卻要幾天才能得到結果。這時候，時間複雜度的分析就顯得必要。

1. 測試結果非常依賴測試環境
   測試環境中硬體的不同會對測試結果有很大的影響。比如，我們拿同樣一份程式碼，分別在 Intel Core i9處理器和 Intel Core i3處理器來執行，肯定 i9比 i3處理器快的多，同樣一份程式碼，在不同的機器上，執行的速度會有不同。
2. 測試介面受資料規模的影響很大
   以排序演算法為例，同一個排序演算法，待排序資料的有序度不一樣，排序的執行時間就會有很大的差別。極端情況，如果資料已經是有序的，那排序演算法的不需要做任何操作，執行時間就會很短，如果測試資料規模調小，測試結果可能無法真實地反應演算法的效能，比如，對於小規模的資料排序，插入排序可能反倒會比快速排序要快！

所以，我們需要一個不用具體的測試資料來測試，就可以粗略地估計演算法的執行效率。

如何進行復雜度分析？

大 O 複雜度表示法

分析一下如下程式碼：

 int cal(int n) {
   int sum = 0;
   int i = 1;
   for (; i <= n; ++i) {
     sum = sum + i;
   }
   return sum;
 }

從 CPU 角度拉看，這段程式碼的每一行都執行的類似的操作：讀資料-運算-寫資料。我們假設沒喊程式碼的執行時間都一樣，為 unit_time。在這個假設基礎之上，這段程式碼總執行時間是多少呢？
第2、3行程式碼分別需要1個 unit_time 的執行時間，第4、5行都運行了 n 遍，所以需要2n*unit_time 的執行時間，所以這段程式碼總的執行時間就是(2n+2)*unit_time。可以看出來。
所有程式碼的執行時間 T(n) 與每行程式碼的執行次數成正比。

 int cal(int n) {
   int sum = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) {
     j = 1;
     for (; j <= n; ++j) {
       sum = sum +  i * j;
     }
   }
 }

我們還是同樣假設每個語句的執行時間是 unit_time，那這段程式碼的總執行時間 T(n) 是多少呢?

第 2、3、4 行程式碼，每行都需要 1 個 unit_time的執行時間，第5、6行程式碼迴圈執行了 n 遍，需要2n * unit_time的執行時間，第7、8行程式碼迴圈執行了 n² 遍，所以需要2n² *unit_time 的執行時間。所以，整段程式碼總的執行時間 T(n)=(2n²+2n+3)*unit_time。
儘管不知道 unit_time 的具體值，但是通過這兩段程式碼執行時間推導，可以得到一個非常重要的規律：
所有程式碼的執行時間 T(n)與每行程式碼的執行次數 n 成正比。
用大 O 複雜度表示法：

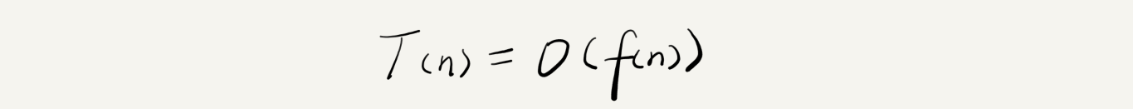
解釋下這個公式：其中，T(n)我們已經講過了，它表示程式碼執行的時間；n 表示資料規模的大小；f(n)表示每行程式碼執行的次數總和，因為這是一個公式，所以用 f(n)來表示。公式中 O，表示程式碼的執行時間T(n) 與 f(n) 表示式成正比。

所以，第一個例子中的 T(n) = O(2n+2)，第二個例子中的 T(n) = O(2n2+2n+3)。這就是大 O 時間複雜度表示法。大 O 時間複雜度實際上並不具體表示程式碼真正的執行時間，而是表示程式碼執行時間隨資料規模增長的變化趨勢，所以，也叫作漸進時間複雜度，簡稱時間複雜度。

公式中低階、常量、係數三部分並部左右增長趨勢，所以可以忽略。用大 O 表示法表示上面兩段程式碼：

   T(n) = O(n) ;  T(n) = O(n^2^)。

時間複雜度分析

1. 只關注迴圈執行次數最多的一段程式碼
   大 O 只是表示一種變化趨勢，通常會忽略公式中低階、常量、係數，只需要記錄一個最大的量級就可以了，所以，我們在分析一個演算法、一段程式碼的時間複雜度的時候，也只關注迴圈執行次數最多的那段程式碼就可以了。
   看下面程式碼：

 int cal(int n) {
   int sum = 0;
   int i = 1;
   for (; i <= n; ++i) {
     sum = sum + i;
   }
   return sum;
 }

第2、3行程式碼都是常量級的執行時間，與 n 的大小無關，迴圈執行次數最多是4、5行，這兩行程式碼被執行了 n 次
，所以總的時間複雜度就是 O(n)。
公式：T(n)=O(max(f(n),g(n)));

2. 加法法則：總複雜度等於量級最大的那段程式碼的複雜度
   在分析如下程式碼：

int cal(int n) {
   int sum_1 = 0;
   int p = 1;
   for (; p < 100; ++p) {
     sum_1 = sum_1 + p;
   }

   int sum_2 = 0;
   int q = 1;
   for (; q < n; ++q) {
     sum_2 = sum_2 + q;
   }
 
   int sum_3 = 0;
   int i = 1;
   int j = 1;
   for (; i <= n; ++i) {
     j = 1; 
     for (; j <= n; ++j) {
       sum_3 = sum_3 +  i * j;
     }
   }
 
   return sum_1 + sum_2 + sum_3;
 }

程式碼分為3部分，分別是 sum_1、sum_2、sum_3。
第一部分時間複雜多多少呢？這段程式碼執行了100次，是一個常量執行時間，跟 n 規模無關，可以忽略。
第二部分和第三部分的時間複雜度分別是 O(n)、O(n²)
綜合這三段程式碼的時間複雜度，取其中量級最大部分，所以整段程式碼的複雜度就為 O(n²)。

3. 乘法法則：巢狀程式碼的複雜度等於巢狀內外程式碼複雜度乘積
   看如下程式碼片段：

int cal(int n) {
   int ret = 0; 
   int i = 1;
   for (; i < n; ++i) {
     ret = ret + f(i);
   } 
 } 
 
 int f(int n) {
  int sum = 0;
  int i = 1;
  for (; i < n; ++i) {
    sum = sum + i;
  } 
  return sum;
 }

落實到具體的程式碼上，我們可以吧乘法法則看成是巢狀迴圈，
f（）函式本身不是一個簡單的操作，它的時間複雜度是 T(n)=O(n)，因為是巢狀函式，所以整個 cal()函式的時間複雜度就是 T(n)=O(n²)=T1(n) * T2(n)。

幾種常見的時間複雜度分析

複雜度量級可以分為多項式量級和非多項式量級。其中，非多項式量級只有兩個：O(2ⁿ) 和 O(n!)。
對於多項式量級，隨著資料規模的增長，演算法的執行時間和空間佔用統一呈多項式規律增長；而對於非多項式量級，隨著資料規模的增長，其時間複雜度會急劇增長，執行時間無限增加；
下面主要來看看幾種常見的多項式時間複雜度：

O(1)

一般情況下，只要演算法中不存在迴圈語句、遞迴語句，即使有成千上萬行的程式碼，其時間複雜度也是Ο(1)。

O(logn)、O(nlogn)

最難分析的是對數階時間複雜度，這裡通過一個例子來說明一下。

 i=1;
 while (i <= n)  {
   i = i * 2;
 }

根據我們前面講的複雜度分析方法，第三行程式碼是迴圈執行次數最多的。所以，我們只要能計算出這行程式碼被執行了多少次，就能知道整段程式碼的時間複雜度。
從程式碼中可以看出，變數 i 的值從 1 開始取，每迴圈一次就乘以 2。當大於 n 時，迴圈結束。還記得我們高中學過的等比數列嗎？實際上，變數 i 的取值就是一個等比數列。如果我把它一個一個列出來，就應該是這個樣子的：

所以，我們只要知道 x 值是多少，就知道這行程式碼執行的次數了。通過 2x=n 求解 x 這個問題我們想高中應該就學過了，我就不多說了。x=log₂n，所以，這段程式碼的時間複雜度就是O(log₂n)。
把程式碼稍微再改一下，你看看這段程式碼的時間複雜度是多少？

 i=1;
 while (i <= n)  {
   i = i * 3;
 }

按照剛才的思路，很簡單就能看出來，這段程式碼的時間複雜度 O(log₃n)。
實際上，不管是以2為底、以3為底，還是以10為底，我們可以把所有對數階的時間複雜度都記為 O（logn)。為什麼呢？
我們知道，對數之間是可以互相轉換的：

log3n 就等於 log₃2 * log₂n，所以 O ( log₃n) = O(C * log₂n)，其中
C=log₃2 是一個常量。

基於我們前面的一個理論：在採用大 O 標記複雜度的時候，可以忽略係數，即 O(Cf(n)) = O(f(n))。所以，O(log2n) 就等於 O(log3n)。因此，在對數階時間複雜度的表示方法裡，我們忽略對數的“底”，統一表示為 O(logn)。

如果你理解了前面講的 O(logn)，那 O(nlogn)就很容易理解了。還記得我們剛講的乘法法則嗎？如果一段程式碼的時間複雜度是 O(logn)，我們迴圈執行 n 遍，時間複雜度就是 O(nlogn) 了。而且，O(nlogn) 也是一種非常常見的演算法時間複雜度。比如，歸併排序、快速排序的時間複雜度都是 O(nlogn)。

O(m+n)、O(m*n)

再來講一種跟前面都不一樣的時間複雜度，程式碼的複雜度由兩個資料的規模來決定。比如：

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

從程式碼中可以看出，m 和 n 是表示兩個未知的資料規模，其大小關係也無法確定，所以我們在表示複雜度的時候，就不能簡單地利用加法法則，省略掉其中一個。所以，上面程式碼的時間複雜度就是 O(m+n)。

針對這種情況，原來的加法法則就不正確了，我們需要將加法規則改為：T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法則繼續有效：T1(m)*T2(n) = O(f(m) * f(n))。

綜上所述：

多項式階：隨著資料規模的增長，演算法的執行時間和空間佔用，按照多項式的比例增長。包括，
O(1)（常數階）、O(logn)（對數階）、O(n)（線性階）、O(nlogn)（線性對數階）、O(n²)（平方階）、O(n³)（立方階）
非多項式階：隨著資料規模的增長，演算法的執行時間和空間佔用暴增，這類演算法效能極差。包括，
O(2ⁿ)（指數階）、O(n!)（階乘階）

空間複雜度分析

相比起時間複雜度分析，空間複雜度分析方法學起來就非常簡單了。

這裡也舉一個例子進行說明：

void print(int n) {
  int i = 0;
  int[] a = new int[n];
  for (i; i <n; ++i) {
    a[i] = i * i;
  }

  for (i = n-1; i >= 0; --i) {
    print out a[i]
  }
}

這裡第 3 行申請了一個大小為 n 的 int 型別陣列，除此之外，其餘程式碼所佔空間都是可以忽略的，所以整段程式碼的空間複雜度就是 O(n)。

我們常見的空間複雜度就是 O(1)、O(n)、O(n^2 )，像 O(logn)、O(nlogn) 這樣的對數階空間複雜度平時都用不到，相比起來，空間複雜度分析比時間複雜度分析要簡單很多。

內容小結

複雜度包括時間複雜度和空間複雜度，用來分析演算法執行效率與資料規模之間的增長關係，越高階複雜度的演算法，執行效率越低。常見的複雜度從低階到高階有：O(1)、O(logn)、O(n)、O(nlogn)、O(n² )。

refer to