你好呀,歡迎你的到來。
首先,已知前序和中序,可以確定唯一一個二叉樹;
已知後序和中序,可以確定唯一一個二叉樹;
此部分內容來自-------------- 作者:Q-WHai 來源:CSDN 原文:https://blog.csdn.net/lemon_tree12138/article/details/49798221?utm_source=copy
具體資料如下:
前序:A B D E H I C F G中序:D B H E I A F C G
1.遞迴重建
在上面的前序序列中,我們可以很容易地獲得A就是根節點。此時,我們可以在後序序列中找到這個A,那麼在A的左邊就是A的左孩子及其子節點,在A的右邊就是A的右孩子及其子節點。假設,我們目前在A的左邊。在遍歷前序序列到B的時候,我就知道了B就是A的左孩子,而在B的左邊(中序序列)的都是B的左孩子及其子節點,在B的右邊(同是也在A的左邊)的就是B的右孩子及其子節點...以此類推.這就是利用遞迴來重建二叉樹。
2.建立節點集
關於這種方法,如果你對B樹有所瞭解,也就不難理解了。因為後面我會單獨寫一篇關於B樹的文章,這裡就暫時一筆代過,說說思路就好了。
為子節點建立節點集。在遍歷(前/後序遍歷的序列)的過程中,分裂和修正這個節點集。
3.建立索引函式
前面的兩種方法,其實可以說是同一種方法,也是比較常見的方法,《程式設計之美》裡使用的正是常見的遞迴呼叫。下面的這種方法是本文的重點,我在其他地方並沒有見到過類似的方法,於是在此記錄一下思路和過程。我當時也只是靈光一閃,想到還可以用這樣巧妙的方法來實現。真是讓人興奮。下面看看具體實現過程。
讓前/後序遍歷的序列擁有中序遍歷序列的索引,在遍歷(前/後序遍歷的序列)的過程中按照二叉排序樹的方法直接插入即可.
圖-4 節點索引函式對照表
看到這個表,是不是有一種似曾相識的感覺。這個在KMP模式匹配也有一個類似的INDEX函式,在KMP裡叫作next.這裡我給他取名叫作index吧。因為這個index很直觀,就是取了某一個節點的下標,並儲存。
其實在已知的遍歷序列中,如果含有中序遍歷結果,那麼我們都可以採用上面的這種建立索引函式的方式來簡化重建過程。可能你會問我為什麼會這樣?下面請看圖-4.
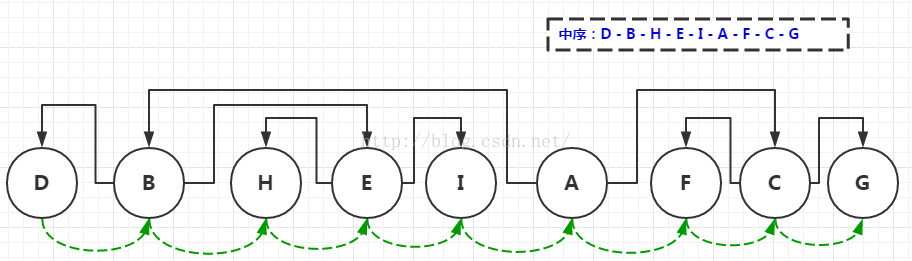
圖-5 二叉樹的中序遍歷順序示意圖
我們可以把圖-2中的中序遍歷二叉樹過程平攤開,就可以獲得圖-5中這樣的一個順序序列。
從上面的圖-5中我們可以發現一個現象,那就是某一個節點的左孩子一定是在這個節點的左邊,其右孩子一定是在這個節點的右邊(當然,這個現象也可以從中序遍歷的定義獲得)。也就是節點Node的左孩子Left的值一定是比Node的值小,而Node右孩子Right的值一定是比Node的值大。
這樣的一些描述是不是似曾相識呢?沒錯,在二叉排序樹中正是這樣定義的。
現在,我們再來看看二叉樹的前序遍歷過程。因為是前序,所以我們在遍歷節點Node的孩子節點之前,必定是已經遍歷過Node的孩子節點。這樣也可以理解成是一種臨近遍歷的過程。
這樣看來,前序 + 中序 = 二叉排序樹。於是,我們就有了以下程式碼:
程式碼:遞迴重建:
import java.util.*;
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
if(pre.length == 0||in.length == 0){
return null;
}
TreeNode node = new TreeNode(pre[0]);
for(int i = 0; i < in.length; i++){
if(pre[0] == in[i]){
node.left = reConstructBinaryTree(Arrays.copyOfRange(pre, 1, i+1), Arrays.copyOfRange(in, 0, i));
node.right = reConstructBinaryTree(Arrays.copyOfRange(pre, i+1, pre.length), Arrays.copyOfRange(in, i+1,in.length));
}
}
return node;
}
}